斐波那契数列的 Python 指南
目录
的斐波那契序列是一个最好的例子递归,学习它是在务实程序员的走向掌握递归之旅的重要一步。尽管您将在本教程中专注于使用 Python 学习它,但您可以将这些概念普遍应用于任何编程语言。
当您对这个著名的递归序列进行深入分析时,它将帮助您更好地掌握和内化递归的主要概念。您甚至会更进一步,学习如何在 Python 中优化斐波那契数列,以及一般的递归算法,从而提高它们的时间效率。
在本教程中,您将学习:
- 什么是斐波那契序列是
- 什么递归是
- 如何使用可调用类优化斐波那契数列
- 如何迭代优化斐波那契数列
- 如何使用调用堆栈可视化递归
要从本教程中获得最大收益,您应该了解Big O 表示法、面向对象编程、Python 的内置方法、控制流语句、函数调用以及列表、队列和堆栈等基本数据结构的基础知识。熟悉这些概念将极大地帮助您理解将在本教程中探索的新概念。
让我们潜入吧!
什么是斐波那契数列?
莱昂纳多·斐波那契是一位意大利数学家,他能够快速回答施瓦本皇帝腓特烈二世提出的这个问题:“一年内获得多少对兔子,不包括死亡案例,假设每对夫妇生下另一对每个月都有一对夫妇,而最年轻的夫妇在生命的第二个月就已经能够繁殖了?”
答案是以下顺序:
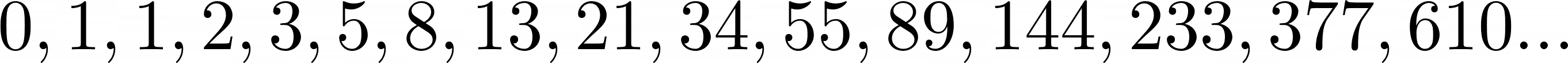
该模式在前两个数字 0 和 1 之后开始,其中序列中的每个数字始终是它前面两个数字的总和。印度数学家从六世纪就知道这个序列,斐波那契利用它来计算兔子数量的增长。
F ( n ) 用于表示第n个月存在的兔子对数,因此序列可以表示为:
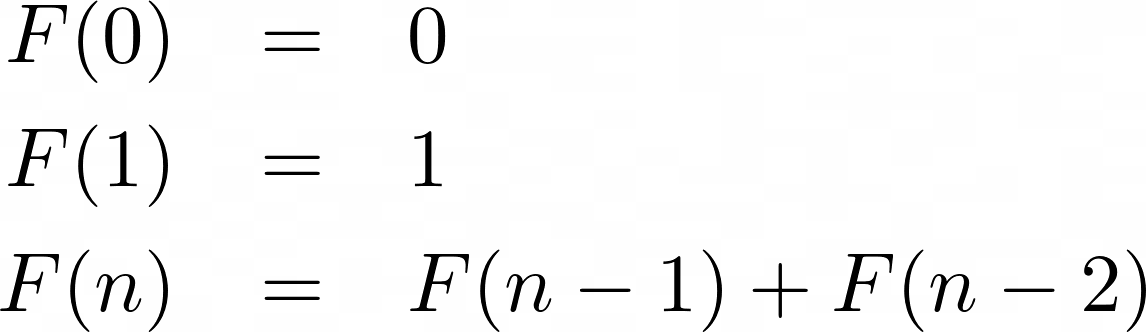
在数学术语中,您可以将其称为递推关系。
还有一个版本的序列,其中前两个数字都是 1,如下所示:
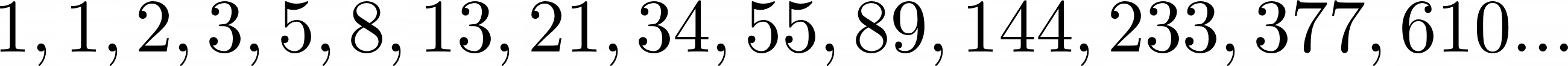
在这种情况下,F (0) 仍然隐式为 0,但您可以从F (1) 和F (2) 开始。该算法保持不变,因为您总是将前两个数字相加以获得序列中的下一个数字。
出于本教程的目的,您将使用以 0 开头的序列。
探索递归
斐波那契数列是一个典型的递归问题。递归是指函数调用自身以分解它试图解决的问题。在每次函数调用中,问题都会变小,直到达到基本情况,然后它将结果返回给每个调用者,直到将最终结果返回给原始调用者。
如果您想计算第五个斐波那契数,F (5),您必须首先计算它的前辈F (4) 和F (3)。为了计算F (4) 和F (3),您需要计算它们的前身。击穿˚F(5)成更小的子问题是这样的:
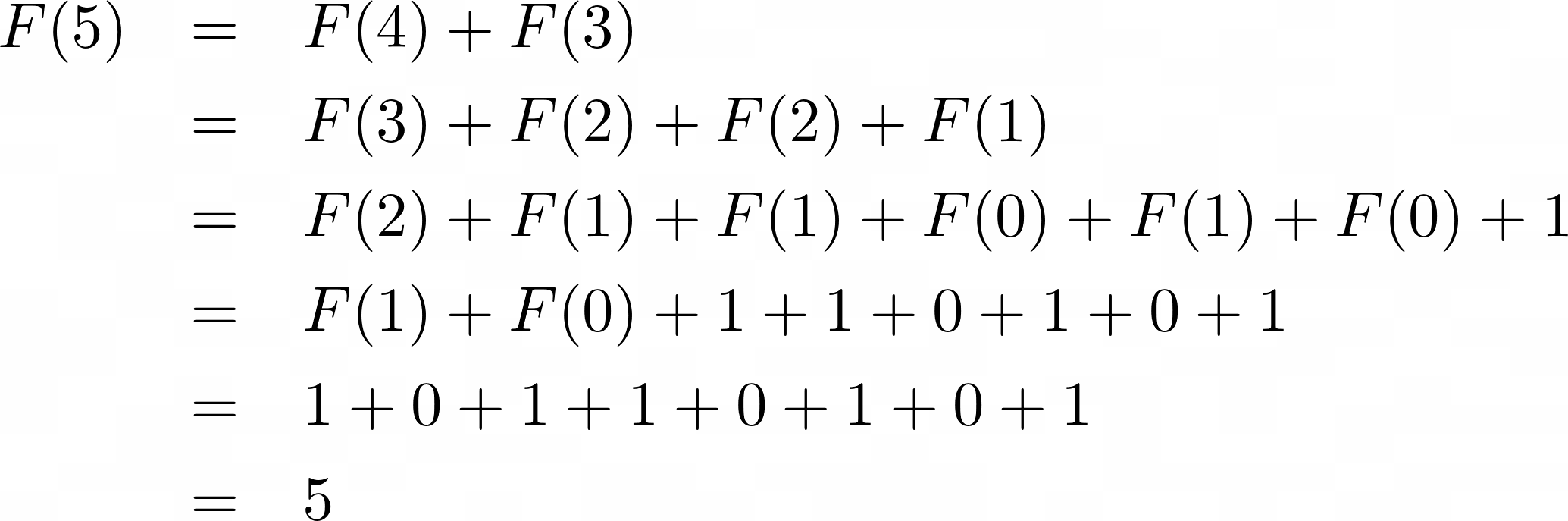
每次调用 Fibonacci 函数时,它都会分解为两个较小的子问题,因为这就是您定义递推关系的方式。当它达到F (0) 或F (1)的基本情况时,它最终可以将结果返回给其调用者。
为了计算斐波那契数列中的第五个数字,您需要解决更小但相同的问题,直到达到基本情况,在那里您可以开始返回结果:
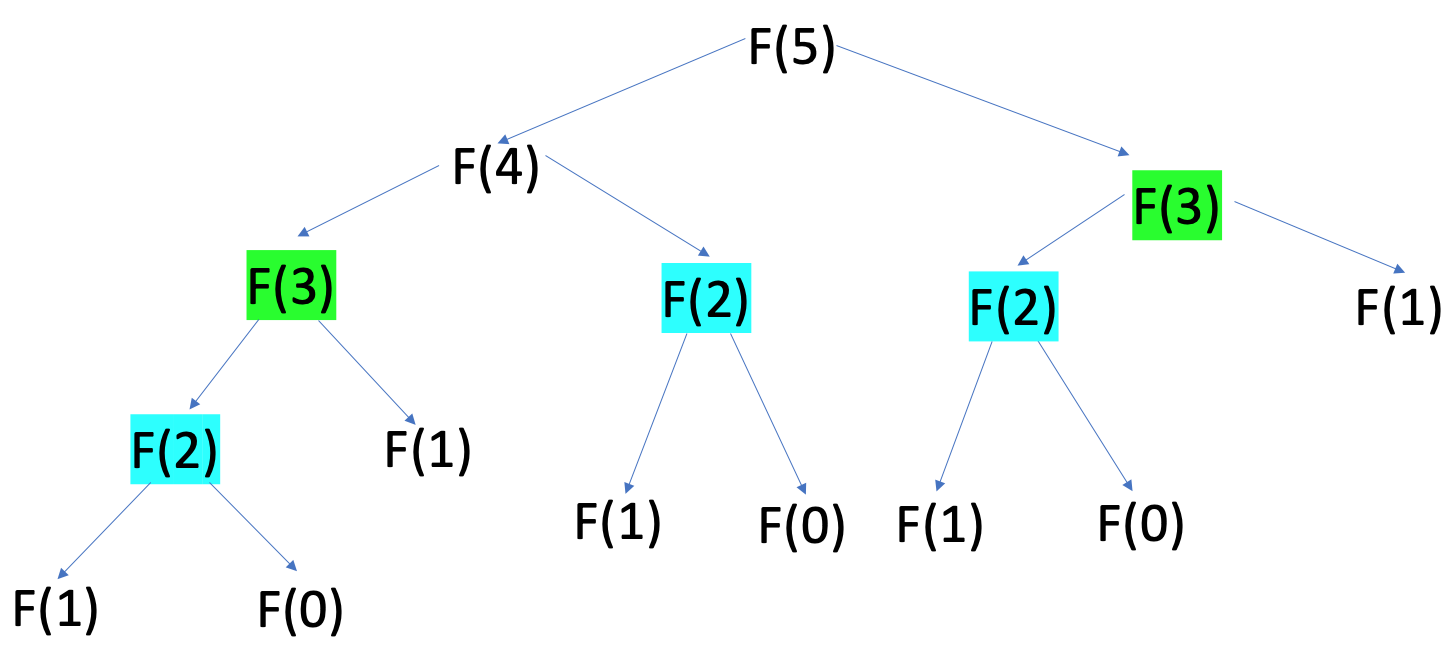
注意上面,您会看到一些相同的子问题以相同的颜色突出显示。您必须在递归中重复计算斐波那契数列中的许多数字。
检查递归斐波那契数列
斐波那契数列最常见和基本的实现如下所示,您fibonacci_sequence()可以根据需要多次调用,直到计算出第n个数字:
def fibonacci_sequence(n):
if n == 0 or n == 1:
return n
else:
return fibonacci_sequence(n-1) + fibonacci_sequence(n-2)
结果,计算非常昂贵,是指数时间,因为您一遍又一遍地计算许多相同的子问题。
在计算F (5) 时,您必须总共对 Fibonacci 函数进行 15 次调用。为了计算F ( n ),调用树的最大深度为n,并且由于每次函数调用都会产生两个额外的函数调用,因此该递归函数的时间复杂度为O (2 n )。
大多数调用都是多余的,因为您已经计算了它们的结果。F (3)出现两次,F (2)出现3次。F (1) 和F (0) 是基本情况,因此多次调用它们是可以的,但是如果您想避免使用递归函数调用它们,那么这也是可能的。您将在后续部分中了解如何消除这些重复调用。
优化斐波那契数列的两种方法
您可以使用两种技术来提高斐波那契数列的效率,或者换言之,减少计算时间。这些技术确保您不会一遍又一遍地计算相同的值,这就是原始算法效率低下的原因。它们被称为记忆化和迭代。
使用记忆
正如您在上面的代码中看到的,您使用相同的输入多次调用 Fibonacci 函数。您可以将前一次调用的结果存储在内存缓存之类的东西中,而不是每次都使用 Fibonacci 函数进行新调用。您可以使用Python 中的列表数据结构来存储先前计算的结果。这种技术称为记忆化。
Memoization 通过将先前计算的结果存储在缓存中来加速昂贵的递归函数调用的计算,因此当再次出现相同的输入时,该函数可以查找该输入的结果并将其返回。您可以将这些结果称为cached或memoized:
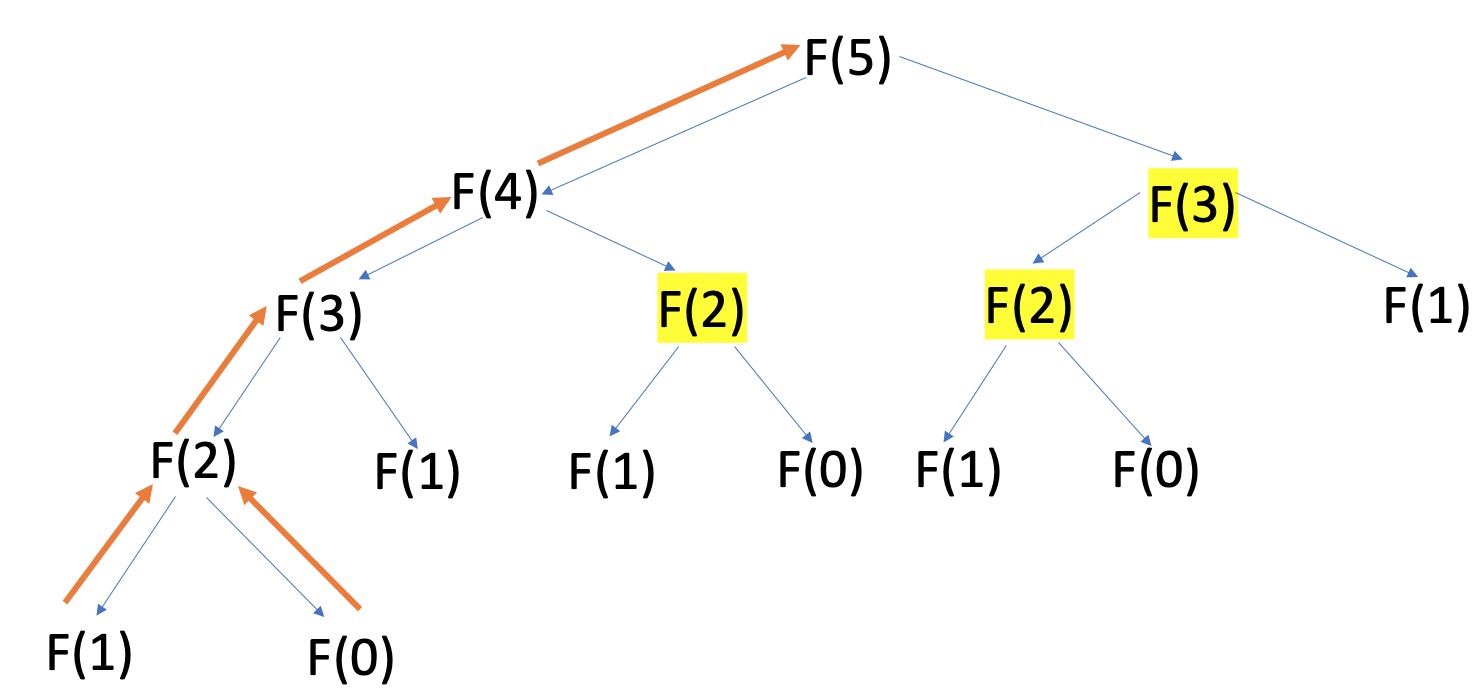
使用记忆功能,您只需在从基本情况返回后遍历深度为n的调用树一次,因为您已经从缓存中检索了所有先前计算的以黄色突出显示的值F (2) 和F (3) .
橙色路径显示斐波那契函数的输入不会被多次调用。这显着降低了算法的时间复杂度,从指数O (2 n ) 到线性O ( n )。
即使对于基本情况,您也可以将调用F (0) 和F (1) 替换为直接从索引 0 和 1 处的缓存中检索值,因此您最终只调用了 6 次函数而不是 15 次!
因为你用0和1的指数为关键字在访问元素这是可能的cache[0]和cache[1]。这些缓存元素将分别存储斐波那契数列的起始值 0 和 1。
使用迭代
如果您根本不需要调用递归斐波那契函数呢?您实际上可以使用迭代算法来计算斐波那契数列中的第n个数字。
您知道序列中的前两个数字是 0 和 1,序列中的每个后续数字都是前两个数字的总和。因此,您实际上可以将前两个数字n - 1 和n - 2迭代地相加,以找到序列中的第n个数字。
紫色粗体数字表示在每个迭代步骤中计算并添加到缓存中的新数字:

您将序列的前两个数字 0 和 1 存储在缓存中,然后将计算结果附加到这个不断增长的缓存中,并cache[n]在您想要计算位置 的斐波那契数时调用n。
Python 中的斐波那契数列:使用可调用类
是时候看看斐波那契数列的这两个优化版本是如何用 Python 表示的了。此代码将斐波那契数列演示为一个可调用类:
1class FibonacciSequence():
2 def __init__(self):
3 self.cache = []
4 self.cache.append(0)
5 self.cache.append(1)
6
7 def __call__(self, i):
8 newfibnum = 0
9
10 # Check input is valid
11 if isinstance(i, int) and i >= 0:
12 # If i is base case of 0 or 1
13 if i == 0 or i == 1:
14 return self.cache[i]
15
16 # If i is NOT stored in the cache already
17 elif i >= len(self.cache):
18 newfibnum = self.__call__(i-1) + self.__call__(i-2)
19 self.cache.append(newfibnum)
20
21 # Previous two values in cache calculates i
22 else:
23 newfibnum = self.cache[i-1]+self.cache[i-2]
24
25 # Return the result of the fib sequence entered by the user
26 return self.cache[i]
27
28 # If input is not valid give error message
29 else:
30 raise ValueError("Invalid input, please enter a positive integer for i")
31
32# Instantiate the FibonacciSequence class
33new_seq = FibonacciSequence()
以下是代码发生的情况的细分:
-
第 2 行
FibonacciSequence使用启动对象.__init__()。缓存是.__init__()构造函数的一部分,这意味着无论何时创建FibonacciSequence对象,都会有一个缓存。该.__init__()构造函数是一个内置的功能,你可以用它来丰富你的类。它有时被称为dunder方法,这是短期的d ouble下得分方法。 -
第 3 行包含下一个内置函数
.__self__(). 它指的是FibonacciSequence类的当前实例。这使您能够访问缓存以存储和检索值。 -
第 7 行有另一个内置函数 ,
.__call__()使您的FibonacciSequence类可调用。一个类可以调用是什么意思?它只是允许像方法一样调用类:>>>>>> new_seq(5) 5您创建并调用
FibonacciSequence名为的类的实例new_seq,并将参数传递给它5。然后new_seq将返回一个值,在这种情况下是斐波那契数列的第五个数字。
Python 中的斐波那契数列:使用非递归函数
此代码实现了上述斐波那契数列的迭代版本:
1def FibonacciSequence(i):
2 # Check whether input is valid
3 if isinstance(i, int) and i >=0:
4 # Initialize the cache with 0, 1
5 cache = []
6 fib_number = 0
7 cache.append(0)
8 cache.append(1)
9 cache_size = len(cache)
10
11 for _ in range(cache_size, i+1):
12 # You're always summing the previous two numbers
13 fib_number = sum(cache[-2:])
14 cache.append(fib_number)
15
16 # Return ith number in fibonacci sequence
17 return cache[i]
18
19 # If input is not valid raise exception
20 else:
21 raise ValueError("Invalid input, please enter a positive integer")
您没有使用任何类型的递归 with FibonacciSequence,并且它在O ( n ) 线性时间内运行。这是一个细分:
-
第 11 行遍历一个
for循环,将前两个数字相加,直到到达缓存的末尾,之后您可以返回斐波那契数列中索引处的数字i。您_对循环变量使用下划线 ( ),因为稍后您将不会在代码中使用此值,因此它是一个一次性变量。 -
第 13 行使用列表符号
[-2:]表示您正在对缓存中的最后两个数字求和。然后,您总是将计算出的这个新数字附加到第 14 行缓存的末尾。 -
ValueError如果函数的输入无效,第 21 行会引发 a 。
记忆斐波那契数列的可视化
使用stacks,您将有效地看到递归函数中的每个调用是如何处理的。每次调用被压入堆栈和弹出的方式正是程序运行的方式,它会清楚地展示如果不优化计算大数将如何花费很长时间。
使用调用堆栈说明可视化
在调用堆栈中,每当函数调用返回结果时,代表函数调用的堆栈帧就会从堆栈中弹出。每当调用函数时,都会在堆栈顶部添加一个新的堆栈帧。
遍历调用堆栈
每个调用堆栈下方的蓝色标签概述了这些步骤。您将逐步了解正在发生的事情,从而帮助您理解递归的基本原理。
您想计算F (5)。为此,您需要在堆栈帧上分配一块内存来一次性存储调用堆栈的所有计算:

请注意,这称为空间复杂度,它是O ( n ),因为一次在帧上的堆栈元素不超过n。
为了计算F (5),您必须按照斐波那契算法的概述计算F (4),因此您将其添加到堆栈中:
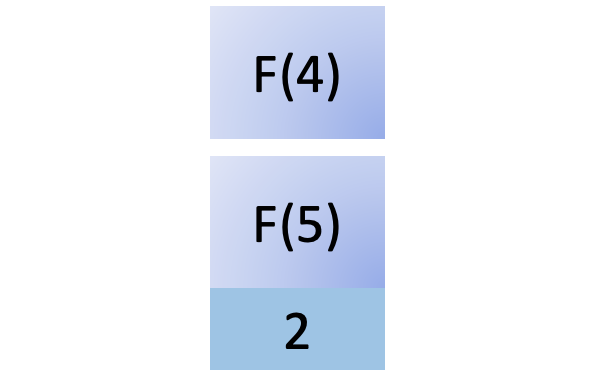
为了计算F (4),您必须计算F (3),因此您将其添加到堆栈中:
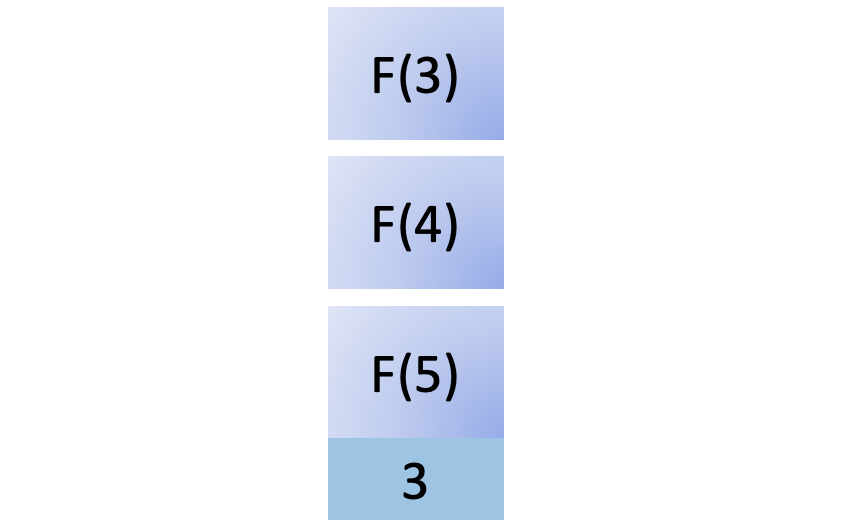
为了计算F (3),您必须计算F (2),因此您将其添加到堆栈中:
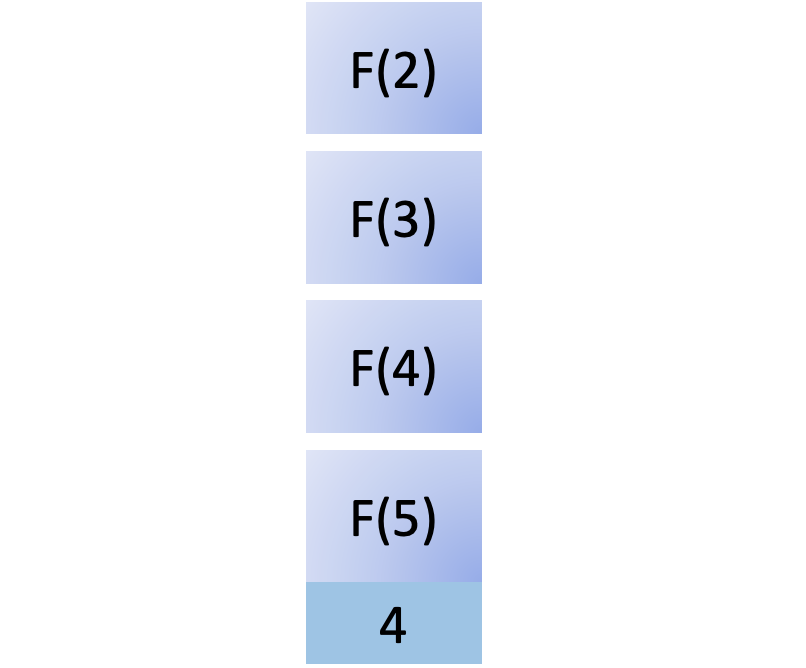
为了计算F (2),您必须计算F (1),即F ( n - 1),因此您将其添加到堆栈中。由于F (1) 是基本情况,它可以立即返回结果,为您提供 1,然后将其从堆栈中删除:
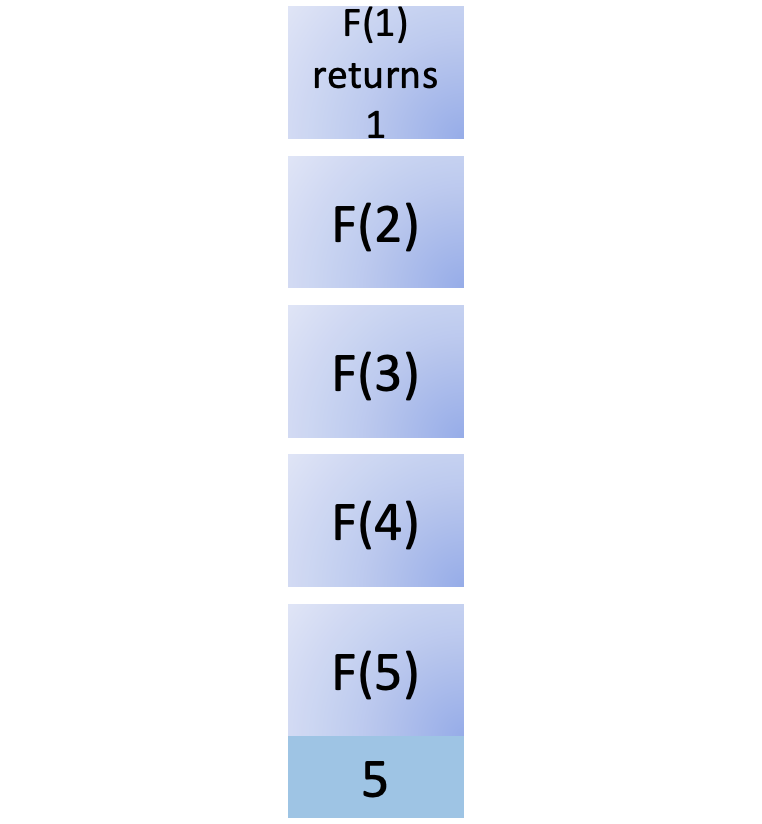
现在您开始递归地展开结果。F (1) 将结果返回给其调用函数F (2)。为了计算F (2),您还需要计算F (0),即F ( n - 2):
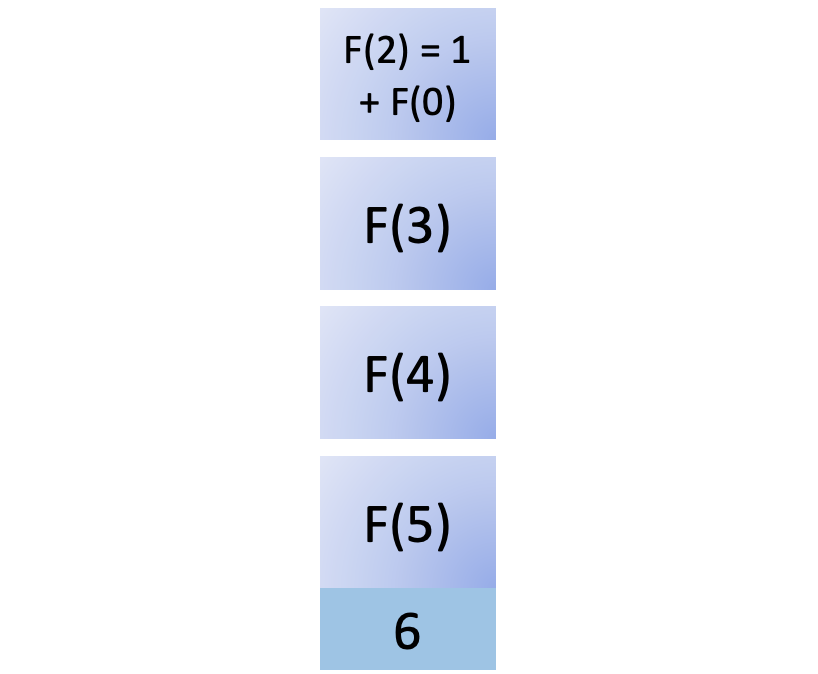
您将F (0)添加到堆栈中。由于F (0) 是基本情况,它可以立即返回结果,为您提供 0,然后将其从堆栈中删除:
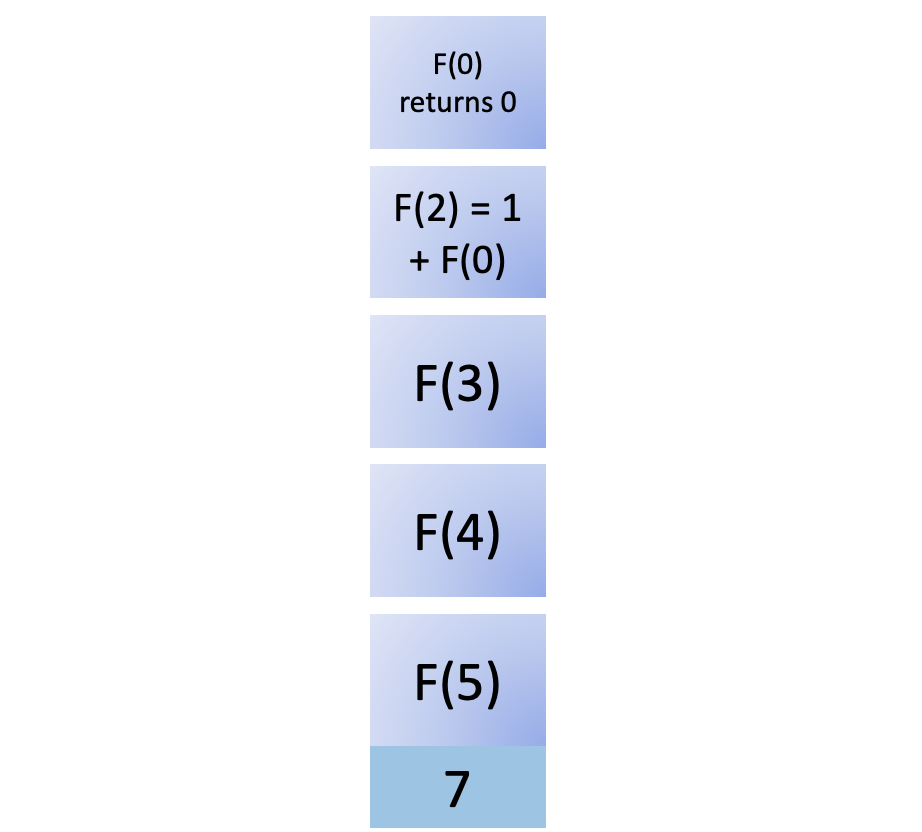
这个结果返回给F (2),现在你有F ( n - 1) 和F ( n - 2) 来计算F (2)。您将F (2)计算为 1 并将其从堆栈中删除:
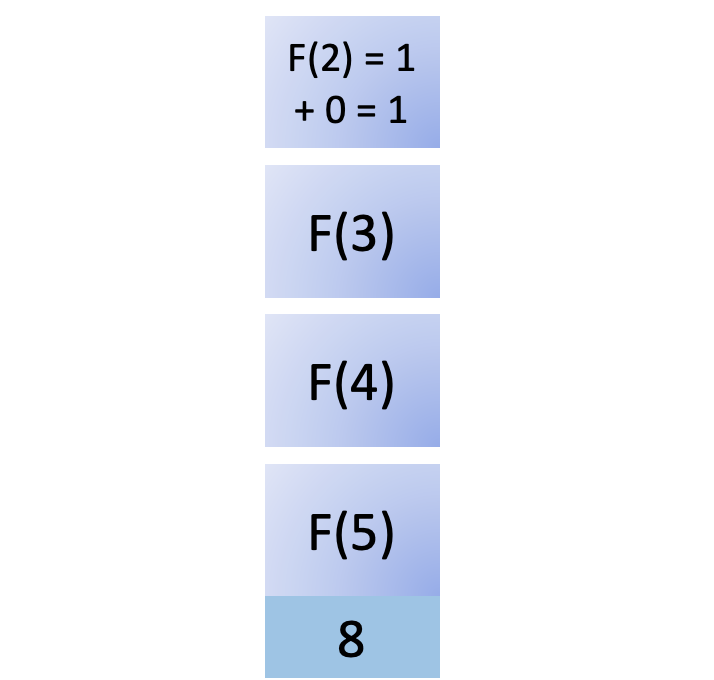
F (2)的结果返回给它的调用者F (3)。F (3)还需要F ( n -2)、F (1)的结果来完成它的计算:
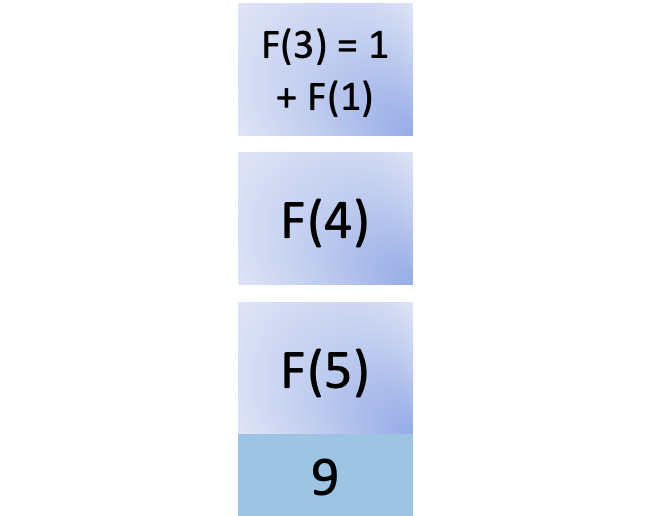
将F (1)的调用添加到堆栈中后,因为它是基本情况并且也在缓存中,您可以立即返回结果并将F (1) 从堆栈中删除:
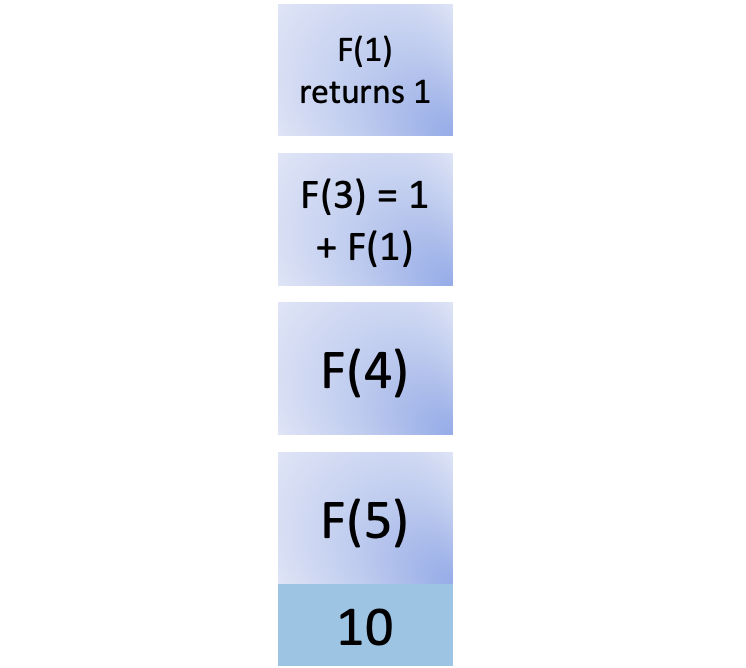
您可以完成F (3)的计算,即 2:
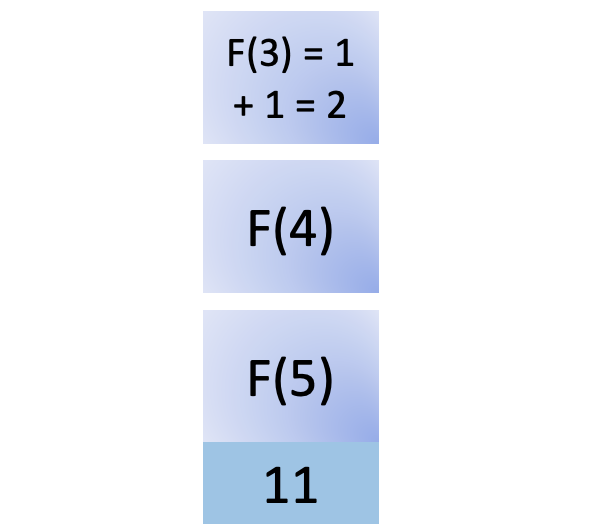
在完成计算后从堆栈中移除F (3) 并将结果返回给它的调用者F (4)。F (4)还需要F ( n -2)、F (2)的结果来完成其计算:

您将F (2)的调用添加到堆栈中。这就是漂亮的缓存的用武之地。您之前已经计算过它,因此您可以通过调用从缓存中检索值cache[2],避免再次递归计算F (2)的结果。它返回 1,然后从堆栈中删除F (2):
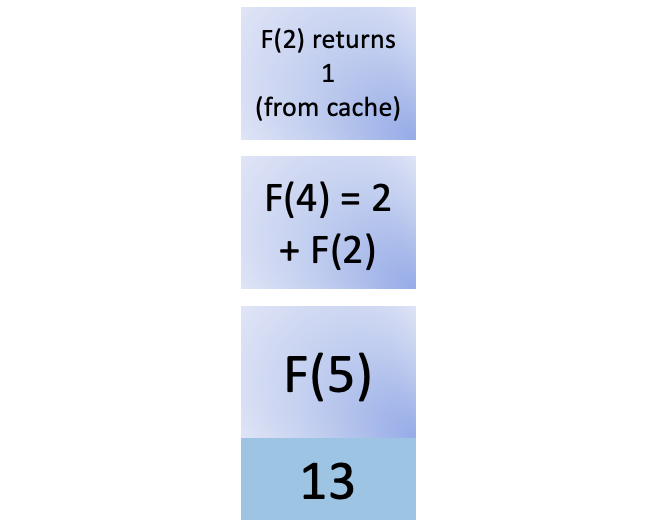
F (2) 返回给它的调用者,现在F (4) 有了它完成计算所需的所有结果,即 3:

您从堆栈中移除F (4) 并将其结果返回给最终的原始调用方F (5):

F (5) 现在有F (4) 的结果,并且还需要F ( n - 2) 的结果,相当于F (3)。
您将F (3)的函数调用添加到堆栈中,漂亮的缓存再次发挥作用。您之前计算了F (3),因此您需要做的就是通过调用从缓存中检索它cache[3],然后您就会得到结果。没有递归过程来计算F (3)。它返回 2,然后从堆栈中删除F (3):
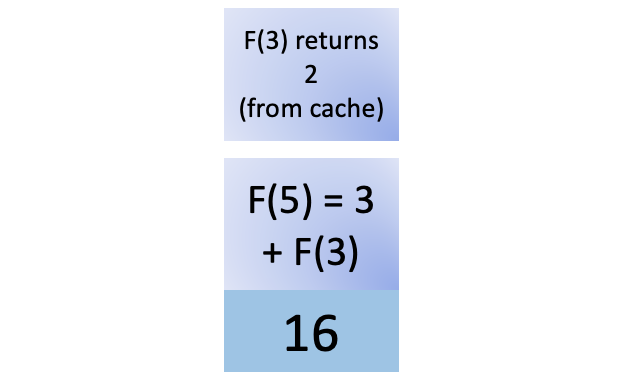
现在F (5) 具有计算结果所需的所有先决条件。将 3 和 2 相加,得到 5,这是从堆栈中弹出F (5)之前的最后一步,结束函数调用:

现在堆栈是空的,因为它已经完成了F (5) 的计算:

将递归函数调用表示为堆栈,可以让您更具体地了解幕后发生的所有工作。它还允许您查看递归函数调用在显示为单个块时占用了多少资源。
将所有这些图像放在一起,这就是堆栈中递归斐波那契数列的完整可视化效果:
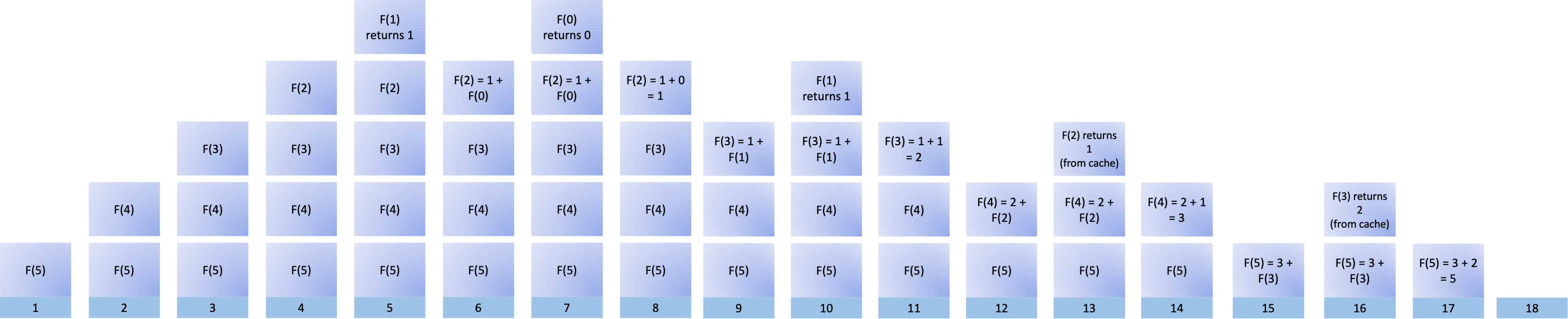
您可以单击上面的图像以放大各个堆栈。从图中可以看出缓存节省了多少计算时间。如果您不存储先前计算的结果,则某些堆栈需要更高,并且将结果返回给各自的调用者需要更长的时间。
结论
您现在已经在 Python 中系统地分析了斐波那契数列,并对这个递归数列的工作原理有了更深入的了解。您还了解到有一些方法可以使用干净的 Pythonic 代码对其进行优化,这在您学习更复杂的递归算法时会很方便。斐波那契数列为您提供了一个极好的跳板和进入递归世界的切入点。
在本教程中,您学习了:
- 什么是斐波那契序列是
- 什么递归是
- 如何使用可调用类优化斐波那契数列
- 如何迭代优化斐波那契数列
- 如何使用调用堆栈可视化递归
一旦您掌握了本教程中涵盖的概念,您的 Python 编程技能将随着您的递归算法思维而提高。
- 点赞
- 收藏
- 关注作者


评论(0)