快速排序算法及其优化

• 一、题目描述
• 二、算法设计与分析
• 三、核心代码
• 四、结果与分析
• 五、总结
• 六、附录（Java源代码）

一、题目描述

当输入数据已经“几乎有序时”，插入排序很快，在实际应用中，我们可以利用这一特点来提高快速排序的速度。当对一个长度小于k的子数组调用快速排序时，让它不做任何排序就返回。当上一层的快速排序调用返回后，对整个数组运行插入排序完成排序过程。证明：这一排序算法的期望时间复杂度为O(nk+nlg(n/k)).分别从理论和实践的角度说明我们应该如何选择k？

###实验环境：
CPU：奔腾 T4300
内存:4G
操作系统：Windows7 ;
软件平台：eclipse

二、算法设计与分析

因为当输入数据已经“几乎有序时”，插入排序很快。快速排序在递归到只有几个元素大小的数组时开始用插入排序的方法。改进的快速排序方法的期望时间=原始快排的期望时间+插入排序方法的期望时间，本实验通过改变k的值来试验出最适合该改进算法的k值。通过理论分析k值大致取值跟logN有关，N为问题规模，于是通过建立一个k变量的for循环，测试出不同k值下优化快排的时间，在用Excel绘制相应的趋势图，用直观的直线图来找出优化后的快排时间随k值变化的变化趋势。

##三、核心代码（以截图的方式展现）

图-1 用随机数生成器初始化用于实验的数组

图-2 主函数中进行普通快排和优化快排

图-3 普通快排函数

图-4优化后的快排函数

图-5 供优化快排调用的子插入快排函数

##四、结果与分析
本次实验中，因为快速排序对于大规模的数据进行排序时优势比较明显。为此，本次实验区较大的问题规模，从而消除快速排序自身排序效率对k取值的影响。为了试验最佳的k值，k的取值范围为[3,199]。下面是取不同问题规模绘制的折线趋势图：

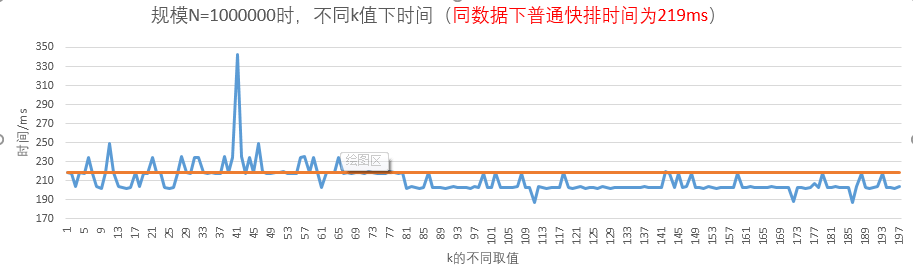
图-6 规模N=1000000时的测试结果

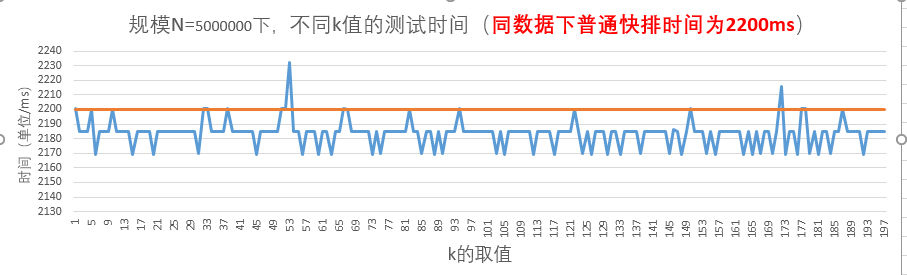
图-7 规模N=5000000时的测试结果

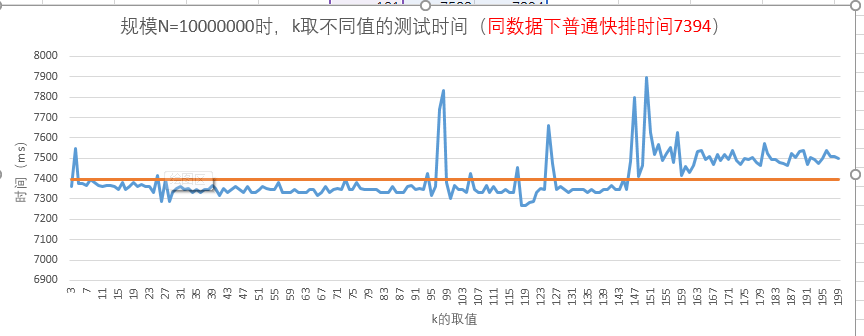
图-8 规模N=10000000时的测试结果

###结果分析

通过将不同规模下的时间数据用Excel进行趋势分析，可以发现采用优化后的快排明显好于普通快排，但会出现极少数离群点（会明显高于普通快排），实验者认为原因可能是测试工具当时出现额外应用突发占用CPU的情况。
不同的问题规模其最佳k值有所不同，且k的取值并不是单一固定的。
当N=1000000时，只有两个离群点（k=53和k=172）大于普通快排的时间开销2200ms，其他都小于2200ms；而最低点较为分散，但k在163-184之间时，最低点分布的较多，所以最佳k应该在这范围内。
当N=5000000时，k<81时，测试时间优化不明显，且波动较大，但当k>81时，时间开销都小于普通快排的时间219；且在k取111、172、189时取最小值。
当N=10000000时，我们发现k取118-121附近时，时间开销最小；而k>146时，时间开销反而比普通快排大。

备注

有可能影响结论的因素：
1、实验设备当前的运行状态，CPU工作状态和内存的使用情况，设备长期运行时需要扇热，会降低CPU使用率。
2、实验设备后台应用的运行状态（运行、阻塞、就绪）对快排程序的影响。
3、测试数据用例的不同，测试用例还不够多，由于时间关系，没有测试多种测试用例并取期望。

##五、总结
1、 总体而言，优化后的快速排序比普通快速排序更优，时间开销更小（除了极个别离群点外，因为离群点可能因为实验设备突发工作状态有关）。
2、 时间开销随k值的变化的规律不是很明显，趋势不单一，更像是周期分布。
3、 当问题规模比较大且k值也很大时，优化的快排时间开销反而比普通快排大。实验者个人认为，其原因在于此时从宏观的角度看，插入排序占据的比例较大，因此时间开销也较大。
4、不同的问题规模的最佳k值不同，但k的最佳取值随问题规模的增大而变小，此规律较难解释，需要后期话时间研究研究。
5、理论上还不解，一些文章中说是 5 到 25 之间。SGI STL 中的快速排序采用的值是 10.

##六、附录（Java源代码）

import java.util.Calendar;

public class quickSort_Optimize {

	/**
	 * @param <Calender>
	 * @param args
	 */
	public static <Calender> void main(String[] args) {
		// TODO Auto-generated method stub int i;
		Sort st=new Sort();
		int arr1[]=new int[st.LEN]; //用于普通的快速排序，来进行比较，同时用于循环执行时赋值给数组arr3；
		int arr2[]=new int[st.LEN]; //优化后快速排序 for(i=0;i<st.LEN;i++)
		{   //用随机数初始化数组arr //让程序产生一个1~100000的随机数； //Math.random()会产生一个0~1的数 int t=(int) (Math.random()*10000); arr1[i]=t; //初始化arr,1，用于普通的快速排序，来进行比较，同时用于循环执行时赋值给数组arr3； arr2[i]=t;
		} long begin=System.currentTimeMillis(); //开始计时
		st.quickSort(arr2 ,0,st.LEN-1); //普通排序函数
		long end=System.currentTimeMillis(); //停止计时
		System.out.println("普通快速排序运行时间："+(end-begin)+"ms"); //for(int k=3;k<Math.log(st.LEN)+20;k++)
		for(int k=3;k<200;k++)
		{ for(i=0;i<st.LEN;i++) {//为了实验的精度，让每使用不同的k值时其排序的原始数组都完全一样； arr2[i]=arr1[i]; } begin=System.currentTimeMillis(); st.quickSort2(arr2 ,0,st.LEN-1,k); //优化的排序函数 end=System.currentTimeMillis(); //System.out.println((end-begin)); System.out.println("k="+k+" 时优化后运行时间："+(end-begin)+"ms");
		} }

}

class Sort
{
	public final static int LEN = 1000000; //类似于C++中的宏定义 public void quickSort(int arr[],int left,int right)
	{//要先判断left<right，否则会出现栈溢出的情况，会出现有j=-1的情况。
		if(left<right) { int i,j; int key=arr[left]; i=left;j=right; while(i<j) { while(arr[j]>=key&&i<j) j--; arr[i]=arr[j]; while(arr[i]<=key&&i<j) i++; arr[j]=arr[i]; } arr[i]=key; //把关键元素放回中间 quickSort(arr,left,i-1); quickSort(arr,j+1,right); }	
	} public void quickSort2(int arr[],int left,int right,int k)
	{
		if(right-left>k) //注意：一定要选判断left<right，否则会出现栈溢出 quickSort(arr,left,right);
		else insertSort(arr,left,right);
	} //优化时调用的子插入排序函数
	public void insertSort(int a[],int left,int right) { for(int i=left;i<right;i++) { int j,key=a[i]; for(j=i-1;a[j]>key;j--) { a[j+1]=a[j]; //把arr[j]向后移动 } a[j+1]=key; } } }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
 

文章来源: blog.csdn.net，作者：allinallinallin，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/to_Baidu/article/details/50283095