详解二叉树的存储王道版（C++/C）
本篇文章结合王道课程及自己对树的理解，希望对你有所帮助
目录
一、树是什么？
1.树的概念
树（Tree）是n（n≥0）个结点的有限集合，当n=0时，为空树；n>0时，为非空树。任意一棵非空树，满足：
（1）有且仅有一个称之为根的结点；
（2)除根结点以外的其余结点可分为m（m＞0）个互不相交的有限集T1, T2, …, Tm, 其中每一个 集合本身又是一棵树，并且称为根的子树（SubTree）。
2.结点的分类
关于树的结点涉及许多概念需要我们了解
结点——结点包含数据元素及若干指向子树的分支信息。
结点的度——结点拥有的子树个数。
树的度——树中结点的最大度数。
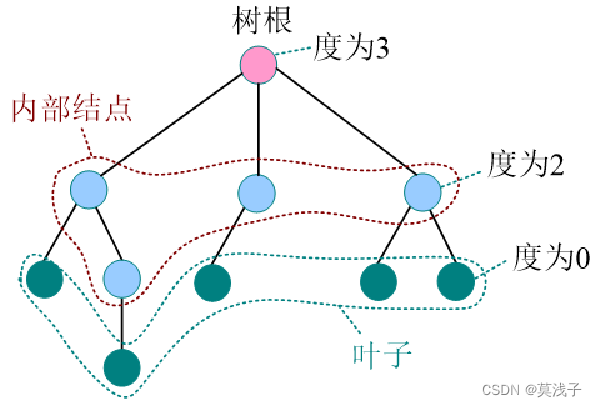
终端结点——度为0的结点，又称叶子。
分支结点——度大于0的结点，除了叶子都是分支结点。
内部结点——除了树根和叶子都是内部结点。
属性
结点的层次（深度）-- 从上往下数（默认从1开始）
结点的高度--从下往上数
数的高度 （深度）-- 总共多少层
结点的度 -- 有几个孩子（分支）
树的度——各结点的度的最大值
3.树的其他相关概念
路径——树中的俩个结点之间的所经过的结点序列。
路径长度——俩接结点之间路径所经过的边数。
双亲、孩子——结点的子树的根称为该结点的孩子。
兄弟——双亲相同的结点互称兄弟。
堂兄弟——双亲是兄弟的结点互称兄弟。
祖先——即从该结点到数根经过的所有结点，称为该结点的祖先。
子孙——结点的子树中的所有结点都称为该节点的子孙。
有序树——逻辑上看，树中结点的各子树从左至右是有次序的，不能互换。
无序树——逻辑上看，树中结点的各子树从左至右是无次序的，可以互换。
森林——森林是m（m>=0） 棵互不相交的树的集合
4.数的存储结构
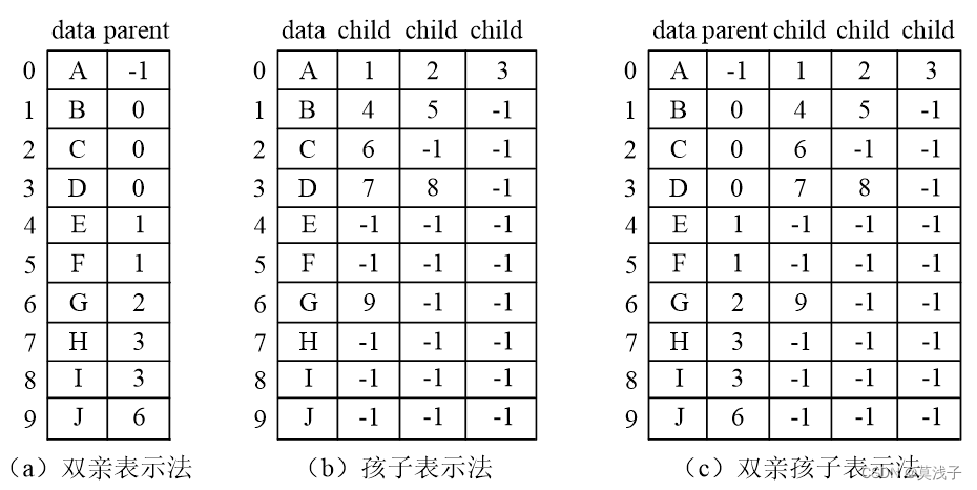
1.双亲表示法
2.孩子表示法
3.双亲孩子表示法
（这里0表示没有）
如果用这个方法会比较浪费空间，而且a,b方法找孩子或者双亲比较麻烦
5、树的常考性质
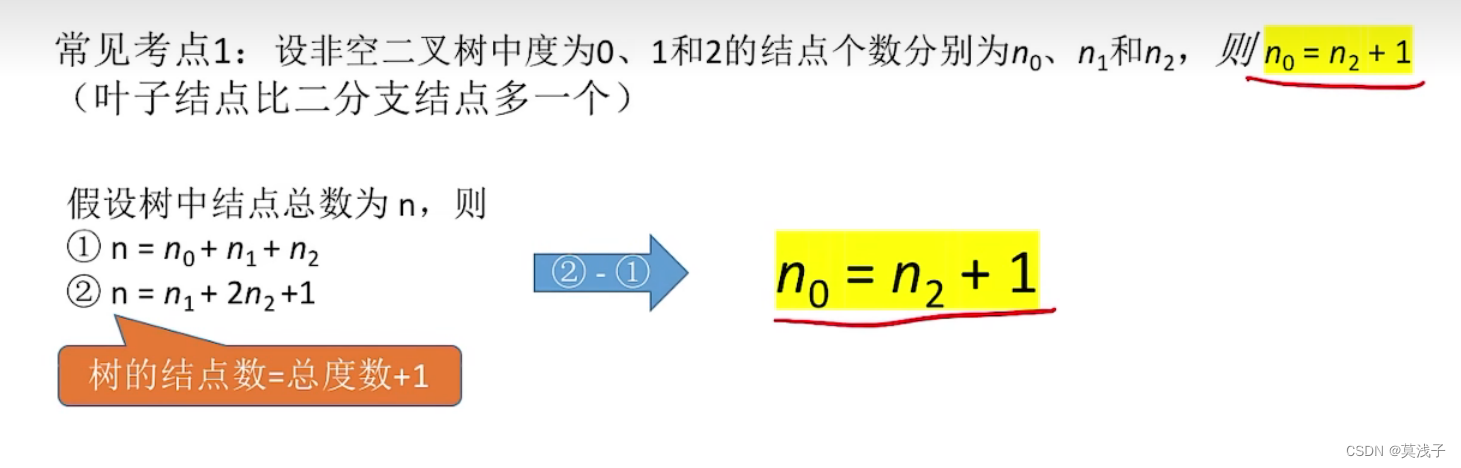
1） 结点数 = 总度数 + 1
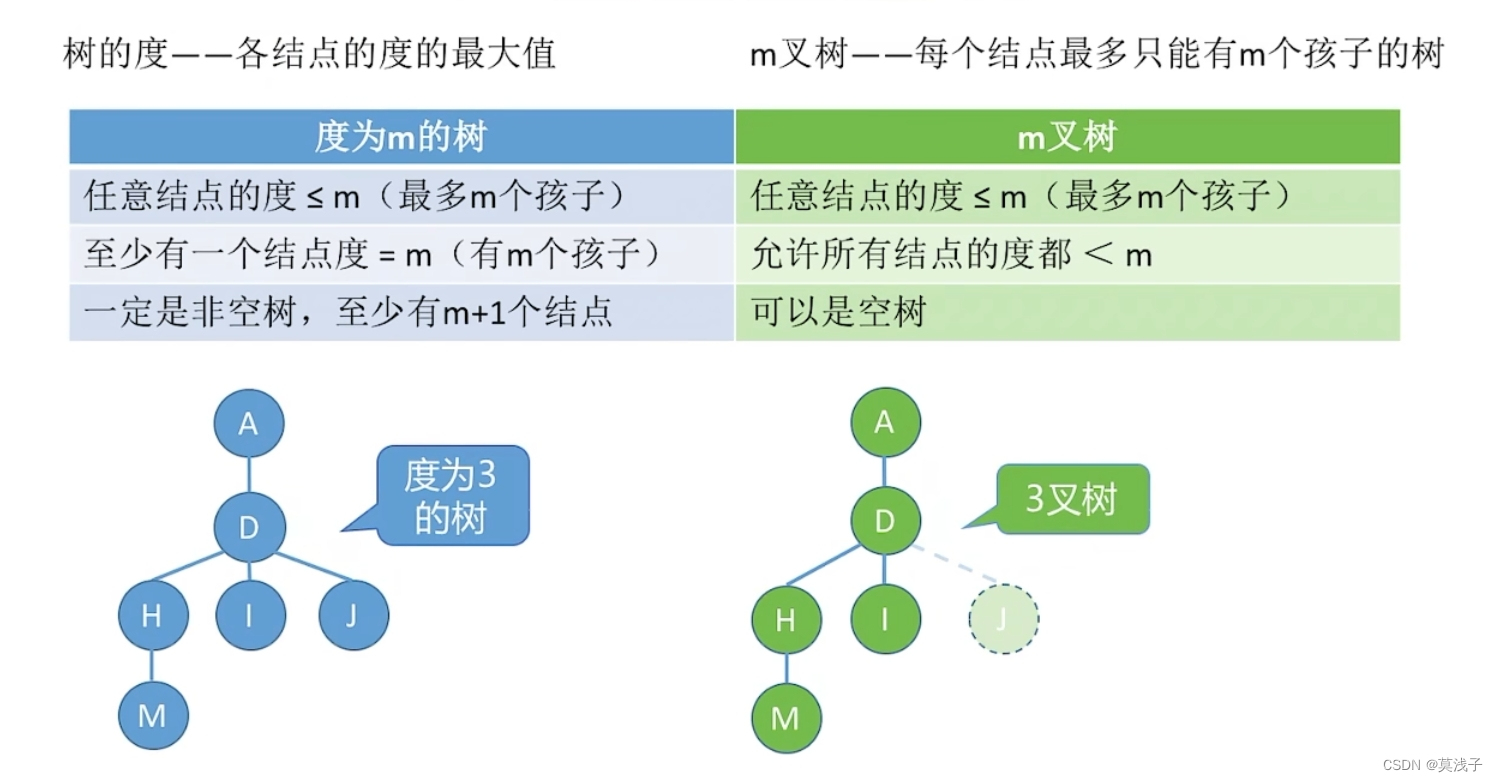
2） 度为m的树，m叉树的区别
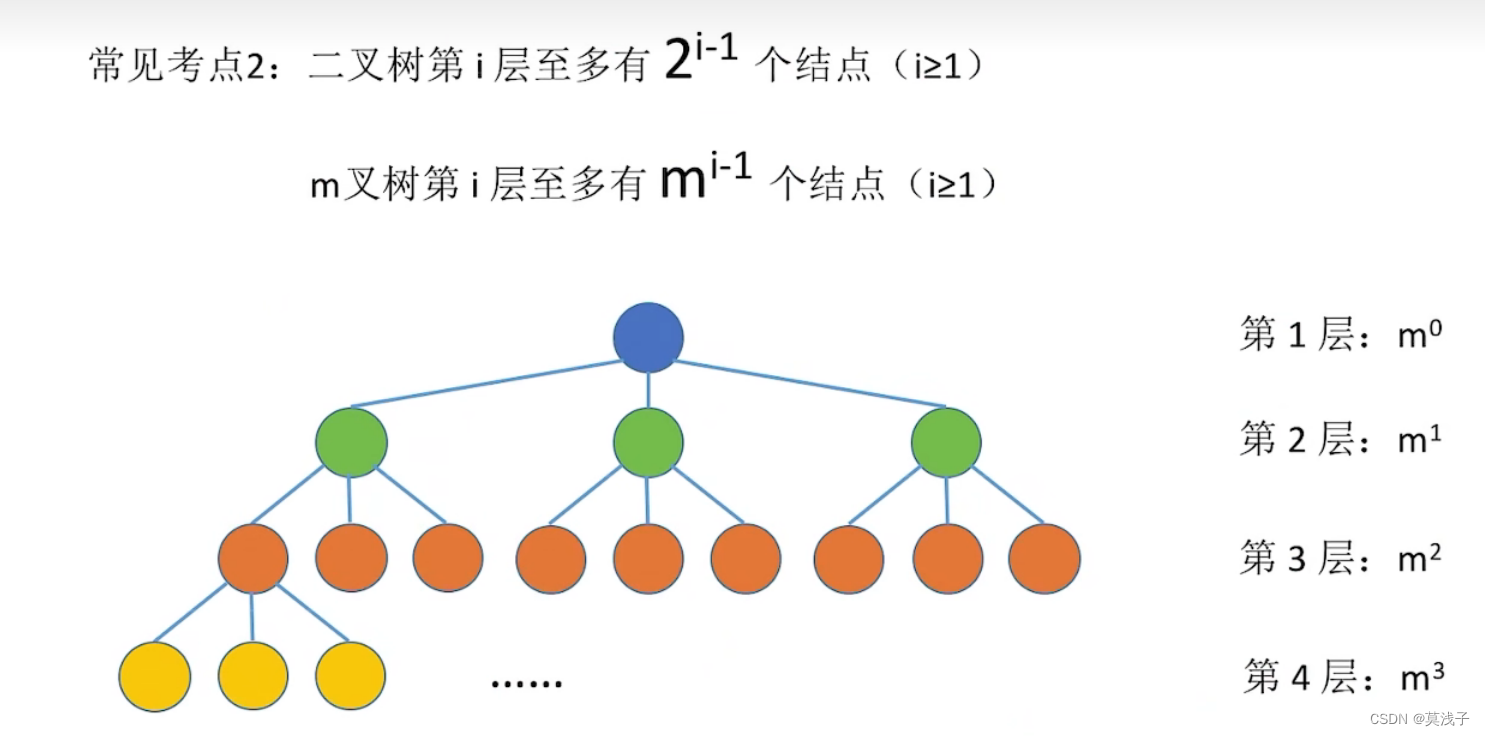
3）度为m的树第 i 层至多有m^i-1 个结点（i>=1）
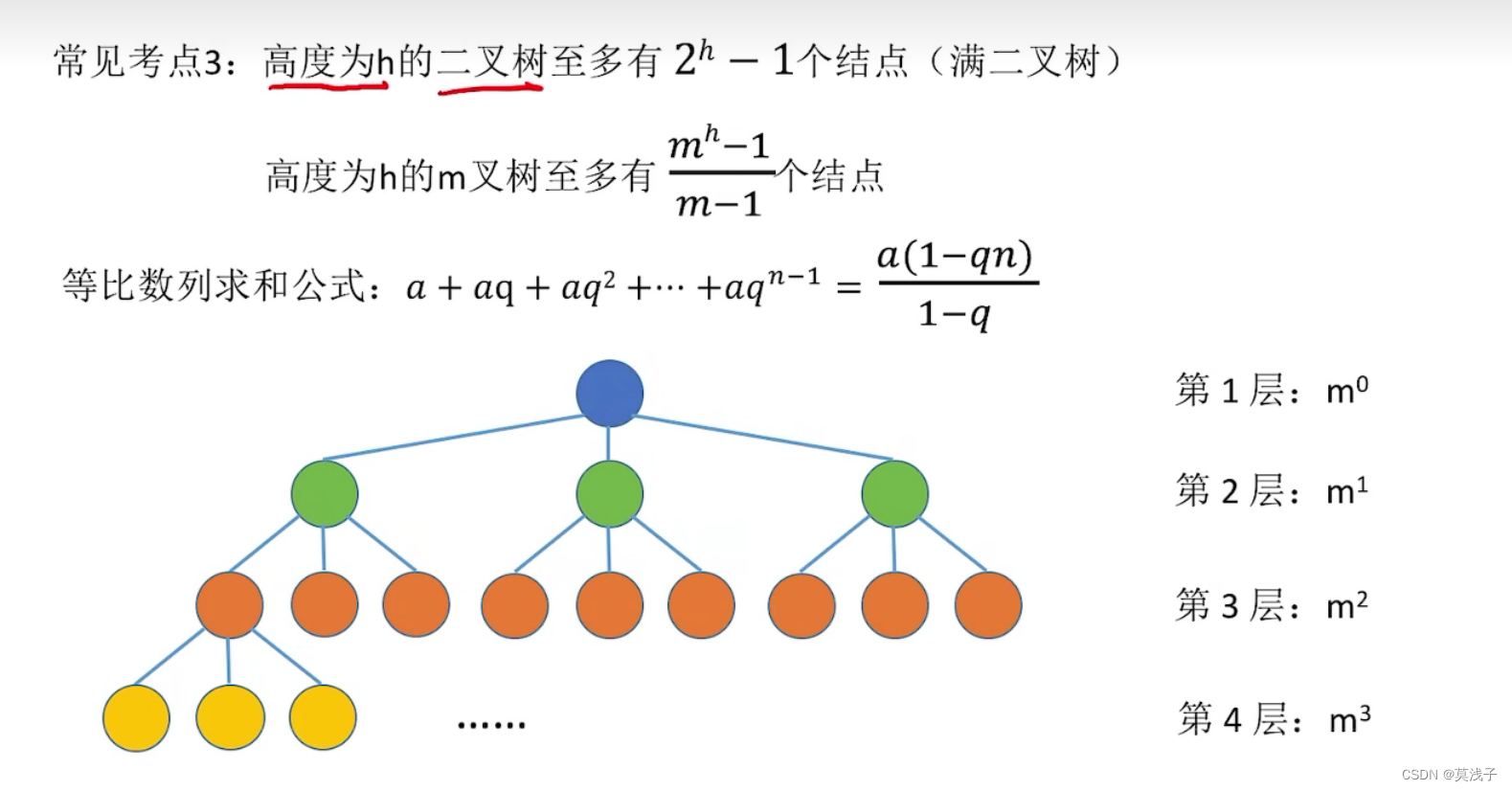
4) 高度为h的m叉树至多有 m^h - 1/ m-1
5) 高度为为h的二叉树至少有h个结点，
高度为h，度为m的树至少有h+m-1个结点。
6) 具有n个结点的m叉树的最小高度为| logm(n(m- 1) + 1)]
二、二叉树
1.如何引入二叉树
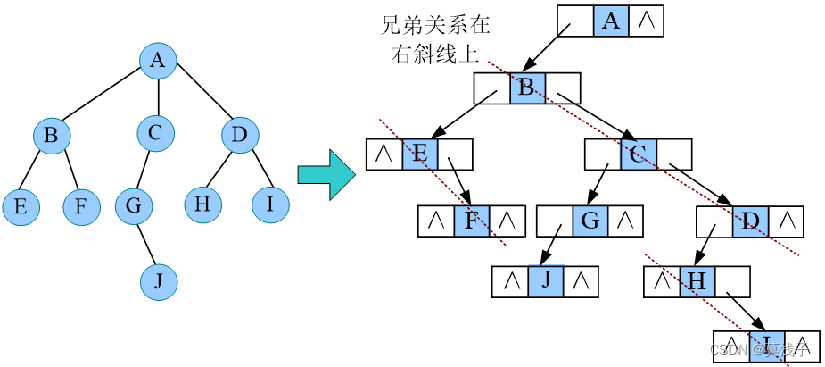
孩子链表示法
孩子兄弟表示法
孩子兄弟表示法秘诀 长子当做左孩子，兄弟关系左右斜
2.相互转换
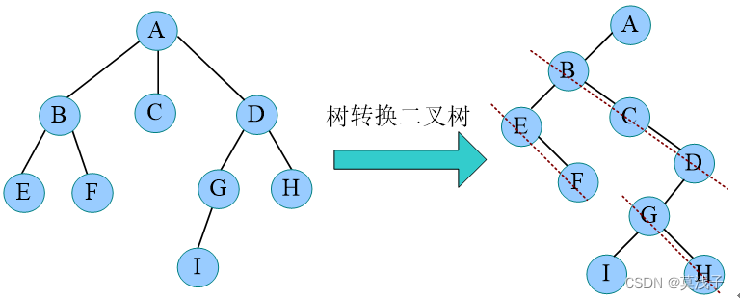
（1）树转换二叉树
（2）二叉树还原为树
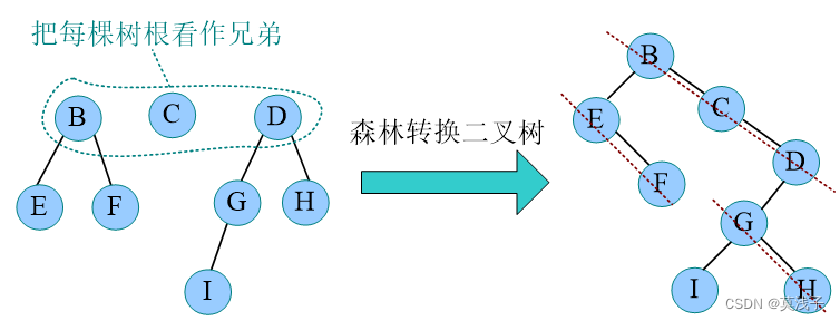
（3） 森林转化为二叉树
3.二叉树概念
二叉树（Binary Tree）是n（n≥0）个结点所构成的集合，它或为空树（n=0）；或为非空树。对于非空树T满足：
（1）有且仅有一个称为根的结点；
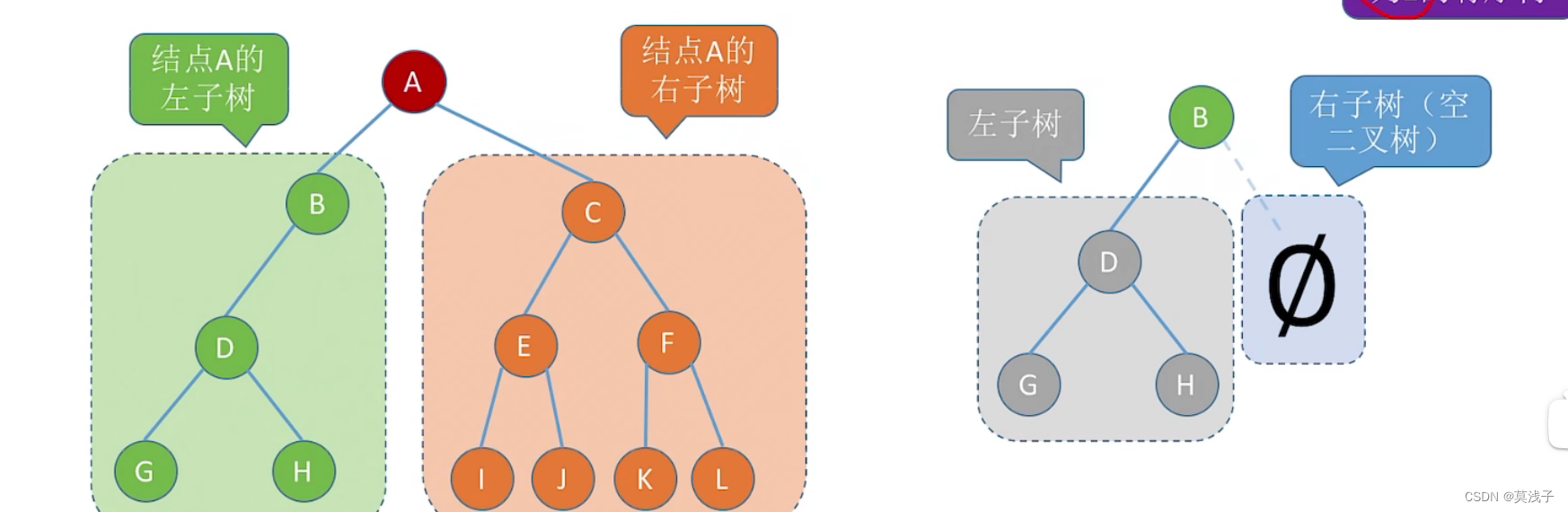
（2）除根结点以外，其余结点分为两个互不相交的子集T1和T2，分别称为T的左子树和右子树，且T1和T2本身都是二叉树
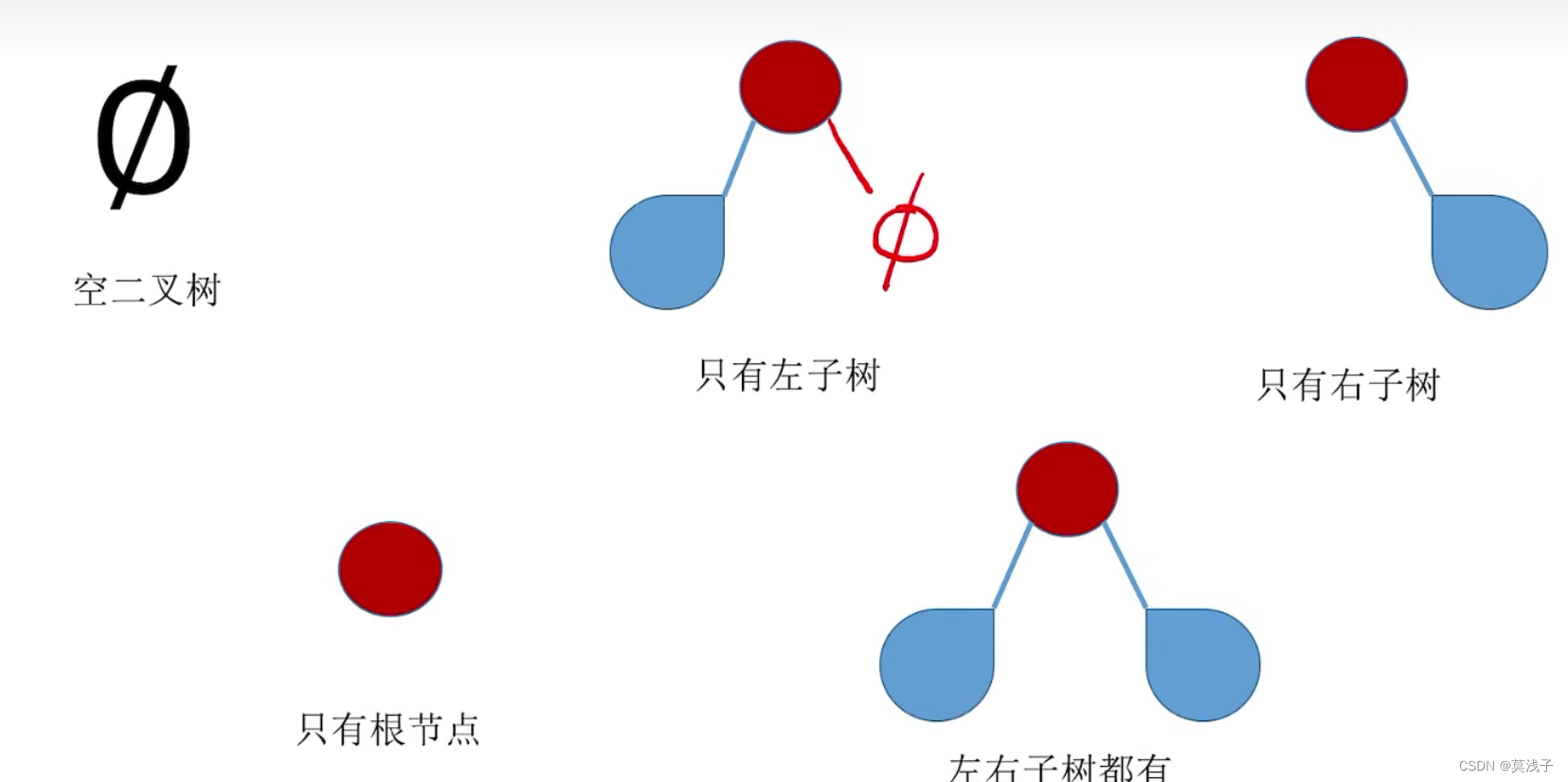
4.二叉树的五种状态
5.几种特殊的二叉树
满二叉树和完全二叉树
如下图（绿色的为叶子结点）
二叉排序树
可以通过二叉排序树快速的进行查找和插入
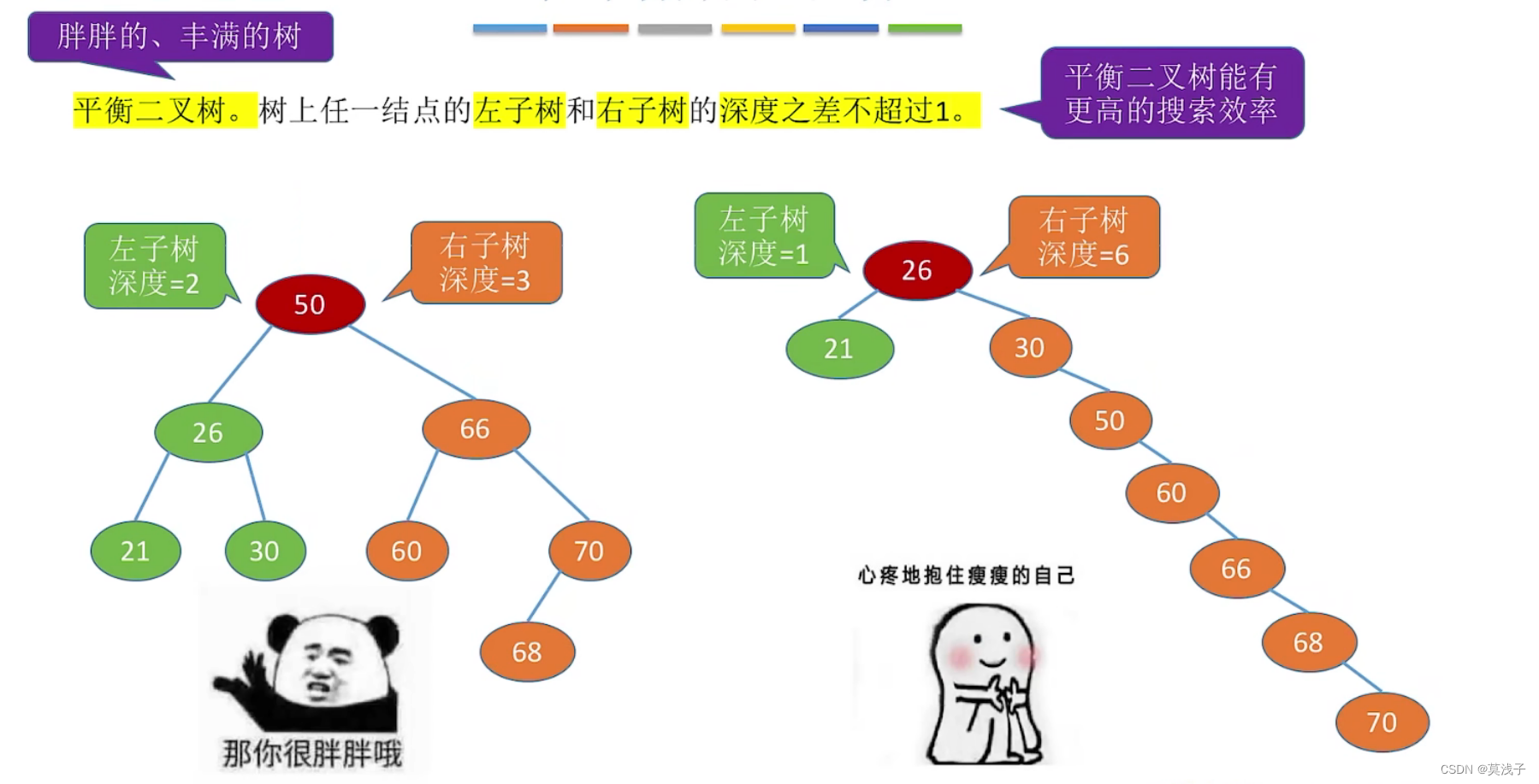
平衡二叉树
6.二叉树的性质
性质1：
性质2：
性质3 ：
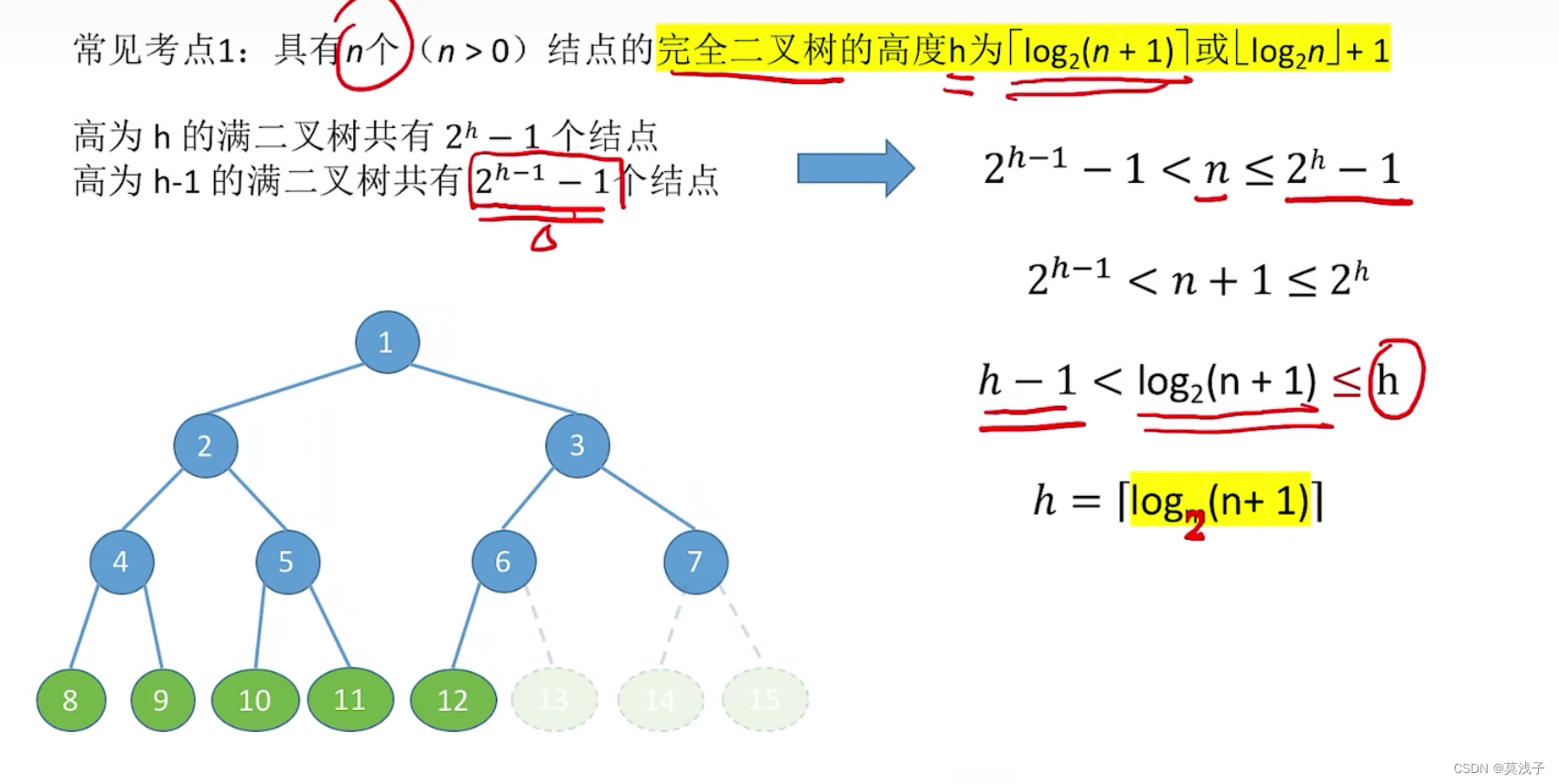
7.完全二叉树的常考性质
考点1：
下面这个符号注意不是绝对值，是向上取整的意思
下面这个符号是向下取整的意思
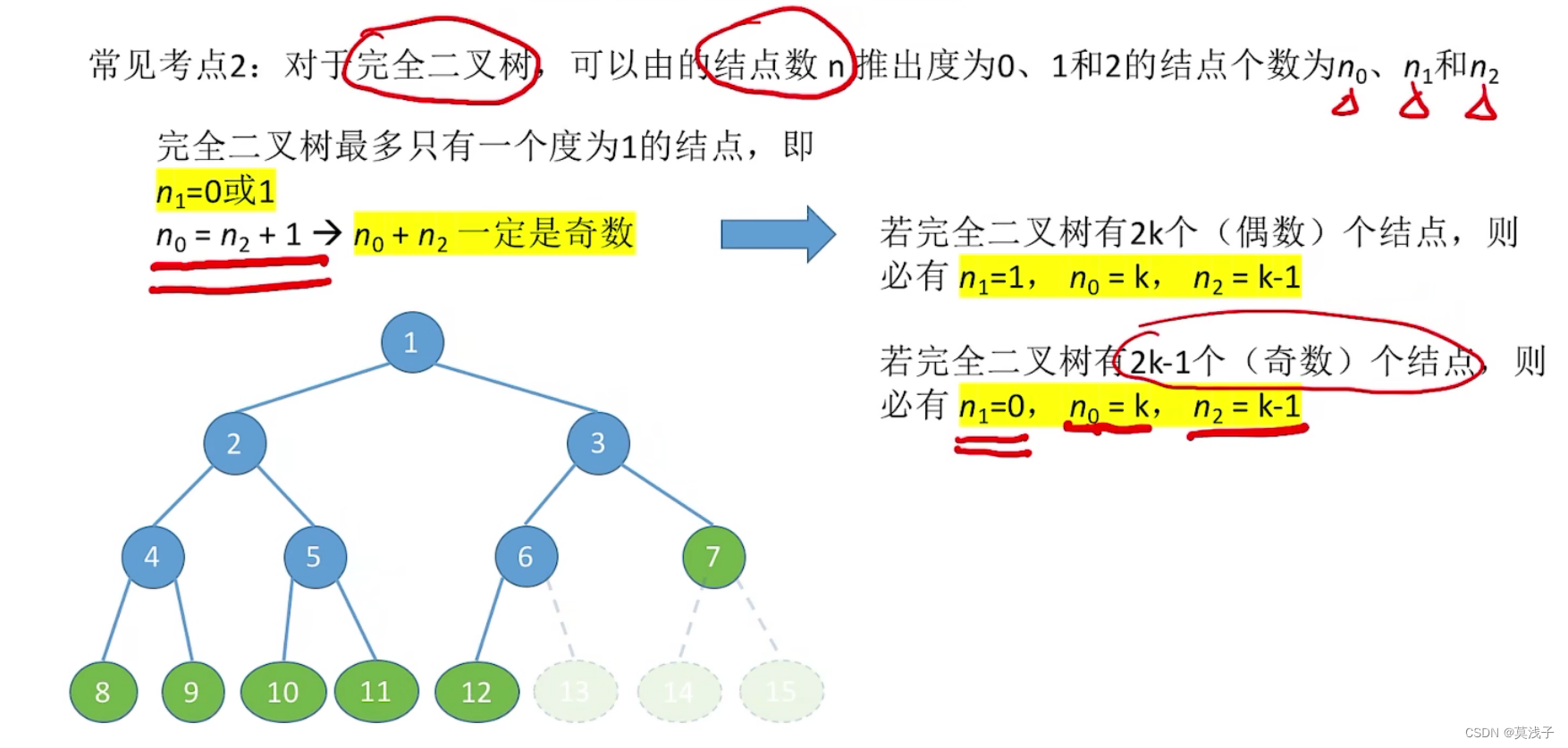
考点2：
总结
二叉树: no= n2+ 1
·第i层至多有2i1个结点（ i≥1)
·高度为h的二叉树至多有2h -1个结点
完全二叉树:
具有n个 （n>0）结点的完全二叉树的高度h为|log,(n + 1)7或Llog2n]+ 1对于完全二叉树，可以由的结点数n推出为0、1和2的结点个数为n、n1和n,(突破点:完全二叉树最多只会有一个度为1的结点)
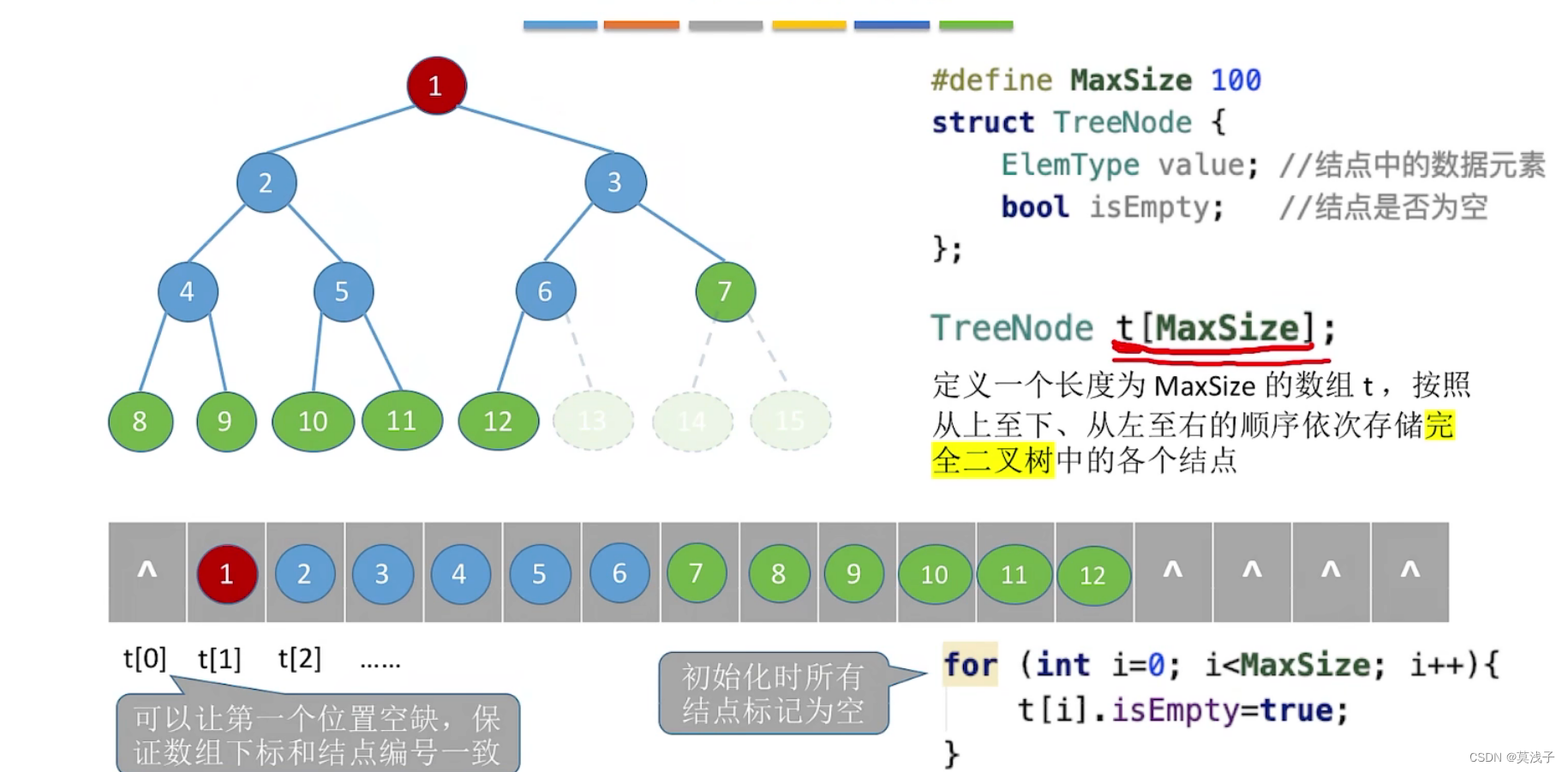
8.二叉树的存储
几个常考的操作
但是如果存储的是非完全二叉树，采用顺序存储会浪费很多空间，所以非完全二叉树基本不考虑这种
代码
struct Elemtype{
int value;
};
//二叉树的结点
typedef struct BiTNode{
Elemtype date; //数据域
struct BiTNode *lchild ,*rchild; //左右孩子指针
}BiTNode ,*BiTree;
//定义一个空树
BiTree root = NULL;
//插入根结点
root = (Bitree) malloc(sizeof(BiTnode));
root->date = {1};
root->lchild = NULL;
root->rchild = NULL;
//插入新的结点
BiTnode *p = (BiTNode *)malloc(sizeof(BiTNode));
p->date = {2};
p->lchild = NULL;
p->rchild = NULL;
root->lchild = p; //作为根结点的左孩子 
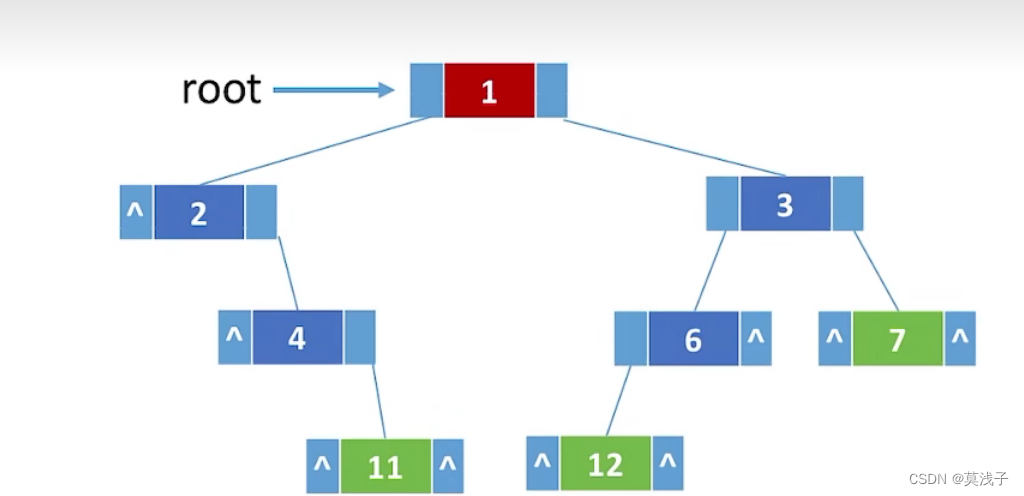
但是这样如果想找到父结点，我们只能从根开始遍历，这样非常浪费时间，我们可以根据题目要求设置一个父结点，也叫三叉链表
typedef struct BiTNode{
Elemtype date; //数据域
struct BiTNode *lchild ,*rchild; //左右孩子指针
struct BiTNode *parent; //父结点
}BiTNode ,*BiTree;
- 点赞
- 收藏
- 关注作者
评论（0）