算法竞赛动态规划篇——数字三角形模型
经典数字三角形问题
题目描述
给定一个如下图所示的数字三角形,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
思路分析
分析:本题是一道非常经典的dp问题,数字三角形问题可以从上往下走来寻找最大路径,也可以从下往上走来寻找最大路径,我们可以发现从上往下走我们要分析每个数是怎么走到这里的,比如0这个数字,只能从左边走过来,右边走不过来,这样我们就多了许多特判的问题,增加了代码的复杂性。我们再看从下往上走的情况,再看0这个数字,它可以走到他下面的任何两个4,这就省略了边界的问题,所以这道题目采用从下到上的方式最为简单,事实上,这也是这道题目的最优解,同学们做题目做多了自然也就掌握了。

C++实现
#include<bits/stdc++.h>
using namespace std;
const int N = 510;//数据范围500
int f[N][N];
int n;
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i ++)
for(int j = 0; j <= i; j ++)
scanf("%d", &f[i][j]);
for(int i = n - 1; i >= 0; i --)
for(int j = 0; j <= i; j ++)
f[i][j] += max(f[i + 1][j], f[i + 1][j + 1]);
printf("%d", f[0][0]);
return 0;
}
注:个人认为下标从0开始更好写代码,从1开始也一样,看个人习惯,这并不影响思路
#include<bits/stdc++.h>
using namespace std;
const int N = 510;//数据范围500
int f[N][N];
int n;
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= i; j ++)
scanf("%d", &f[i][j]);
for(int i = n - 1; i >= 0; i --)
for(int j = 1; j <= i; j ++)
f[i][j] += max(f[i + 1][j], f[i + 1][j + 1]);
printf("%d", f[1][1]);
return 0;
}
摘花生
题目描述
Hello Kitty想摘点花生送给她喜欢的米老鼠。
她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。
地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走,不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。

思路分析
分析:经过经典数字三角形问题,我们很容易就理解了其中相似的思考方式,每个点只能从左边来或者从上边来,也是一个典型的dp问题

C++实现
#include <bits/stdc++.h>
using namespace std;
const int N = 110;//数据范围
int w[N][N], f[N][N];
int n, m;
int main()
{
int T;//T组数据
scanf("%d", &T);
while(T --)
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
scanf("%d", &w[i][j]);
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];
printf("%d\n", f[n][m]);
}
return 0;
}
最低通行费
题目描述
一个商人穿过一个 N×NN×N 的正方形的网格,去参加一个非常重要的商务活动。
他要从网格的左上角进,右下角出。
每穿越中间 11 个小方格,都要花费 11 个单位时间。
商人必须在 (2N−1)(2N−1) 个单位时间穿越出去。
而在经过中间的每个小方格时,都需要缴纳一定的费用。
这个商人期望在规定时间内用最少费用穿越出去。
请问至少需要多少费用?
注意:不能对角穿越各个小方格(即,只能向上下左右四个方向移动且不能离开网格)。
思路分析1
分析:经过上面两道题目的学习,我们很容易发现这道题目是摘花生的进阶,本质上差不多,摘花生是求max,最低通行费是求min,分析思路也与上面完全一样,所以这里就不画dp分析了,需要注意的是2n - 1是什么,很容易分析,如下图,可以看到不是就是两个边长减去1,也就是红格子,稍微一分析就发现和摘花生完全一样,只能从左上角走到右下角,而且每次只能往右走或者往下走。

与摘花生不一样的最小值怎么分析,若一味的把上面的代码照搬下来肯定是错误的,原因在这里,看上面的绿格子,它只能从左边来,不能从上边来,从上边来的话上边初始化为0,经过min的运算,肯定是选择了上面的格子,答案肯定错,但是摘花生的max就不会出现这种情况。
C++实现1
#include <bits/stdc++.h>
using namespace std;
const int N = 110, INF = 1e9;
int n;
int w[N][N], f[N][N];
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
scanf("%d", &w[i][j]);
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
{
if(i == 1 && j == 1) f[i][j] = w[i][j];//对第一个格子特判
else
{
//对于所有的格子,一定能更新,但要注意边界
f[i][j] = INF;//所有格子初始化最大值
if(i > 1) f[i][j] = min(f[i][j], f[i - 1][j] + w[i][j]);//如果不是第一行,可以从上面走下来
if(j > 1) f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]);//如果不是第一列,可以从下面走下来
}
}
printf("%d", f[n][n]);
return 0;
}
思路分析2
分析:针对思路分析1,我们可以看到代码描述如上,与摘花生的代码有些许不同,特判的条件太多,我们还是不希望这样的事情发生,所以我们针对上面的问题,来一个初始化数组正无穷的操作。
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n;
int w[N][N], f[N][N];
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
scanf("%d", &w[i][j]);
memset(f, 0x3f, sizeof f);//将数组初始化为正无穷
f[1][1] = w[1][1]; //对左上角元素特殊处理
for (int i = 1; i <= n; i ++)
{
for (int j = 1; j <= n; j ++)
{
f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]);
f[i][j] = min(f[i][j], f[i - 1][j] + w[i][j]);
}
}
printf("%d", f[n][n]);
return 0;
}
ps:最开始初始化我没有想到memset,我想到的是把f数组都初始化为一个较大的数,但答案是错误的,这里给大家演示一下
#include <bits/stdc++.h>
using namespace std;
const int N = 5;
int main()
{
int f[N] = {4};
for(int i = 0; i < N; i ++)
printf("%d ", f[i]);
return 0;
}
//4 0 0 0 0
我们想把它全部初始化为某一个数,这样做只会初始化第一个数,所以如果还是要初始化为某一个数,得用for循环。
方格取数
题目描述
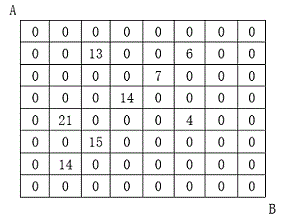
设有 N×N 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字0。如下图所示:
某人从图中的左上角 A 出发,可以向下行走,也可以向右行走,直到到达右下角的 B 点。
在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从 A 点到 B 点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。
思路分析
分析:此题与摘花生不同的是走两次,可以走两次来进行,走过的将数字重置为0。在这里我们介绍同时走的方法。

这里要考虑一个问题,这两个格子是否是同一个格子,如果是,那么加一个格子,如果不是,那么两个格子的数都相加
C++实现
#include <bits/stdc++.h>
using namespace std;
const int N = 15;
int w[N][N];
int f[N + N][N][N];
int main()
{
int n;
scanf("%d", &n);
int a, b, c;
while(cin >> a >> b >> c, a || b || c) w[a][b] = c;
for(int k = 2; k <= n + n; k ++)
for(int i1 = 1; i1 <= n; i1 ++)
for(int i2 = 1; i2 <= n; i2 ++)
{
int j1 = k - i1, j2 = k - i2;
if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
{
int t = w[i1][j1];
if(i1 != i2) t += w[i2][j2];
int &x = f[k][i1][i2];
x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
x = max(x, f[k - 1][i1 - 1][i2] + t);
x = max(x, f[k - 1][i1][i2 - 1] + t);
x = max(x, f[k - 1][i1][i2] + t);
}
}
printf("%d", f[n + n][n][n]);
return 0;
}
我们看到核心部分的代码过于冗长,可以将其进行简化
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 15;
int n;
int w[N][N];
int f[2 * N][N][N];
int main()
{
cin >> n;
int a, b, c;
while(cin >> a >> b >> c, a || b || c) w[a][b] = c;
for(int k = 2; k <= n + n; k ++)
for(int i1 = 1; i1 <= n; i1 ++)
for(int i2 = 1; i2 <= n; i2 ++)
{
int j1 = k - i1, j2 = k - i2;
if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
{
int t = w[i1][j1];
if(i1 != i2) t += w[i2][j2];
int &x = f[k][i1][i2];
for(int a = 0; a <= 1; a ++)
for(int b = 0; b <= 1; b++)
x = max(x, f[k - 1][i1 - a][i2 - b] +t);
// x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
// x = max(x, f[k - 1][i1][i2 - 1] + t);
// x = max(x, f[k - 1][i1 - 1][i2] + t);
// x = max(x, f[k - 1][i1][i2] + t);
}
}
printf("%d\n", f[n + n][n][n]);
return 0;
}
总结
数字三角形问题是dp当中一个简单的模型,我们可以看到取max时,数组初始化0;取min时,数组用memset初始化更优;另外,属性除了max和min,有时候还会出现数量。
- 点赞
- 收藏
- 关注作者


评论(0)