深度学习入门之感知机
【摘要】 深度学习入门第二章
感知机(perceptron)是神经网络起源的算法
感知机是什么
感知机接收多个信号,输出一个信号(0不传递信号,1传递信号)

输入信号x1,x2,乘以固定的权重w1,w2,如果总和超过了某个界限值,则会输出1,否则为0,用底下数学式来表示:
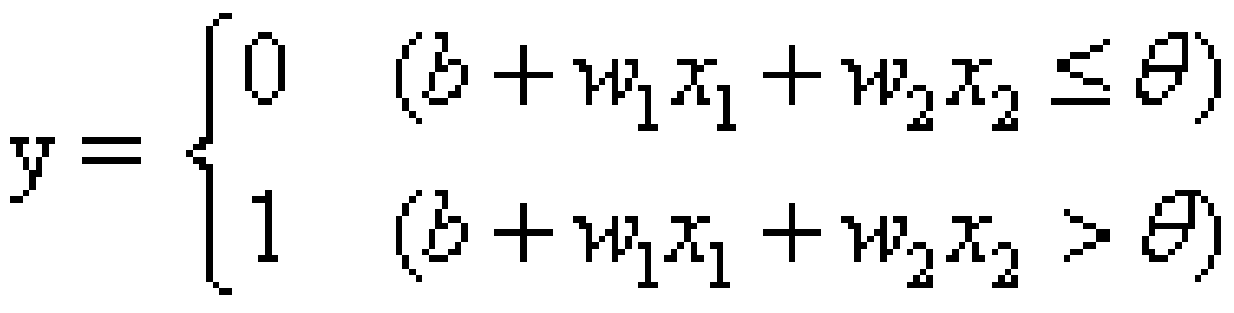
不知道为啥mathtype保存的图片放大就有点模糊了

总之,感知机的运行原理就是这个,多个输入信号都有自己的权重。权重越大,对信号重要性越高
简单逻辑电路
与门
两个输入均为1的时候输出1,否则为0
比如说当(w1,w2,θ)=(0.5,0.5,0.7)时,就满足与门的条件
与非门和或门
与非门就是颠倒与门的输出,,只有x1,x2同为1的时候输出0,其他时候输出1,可以采用(w1,w2,θ)=(-0.5,-0.5,-0.7)这种组合
或门是只要有1就输出1,可以采取(w1,w2,θ)=(1.0,1.0,0.8)组合
感知机的实现
def AND(x1,x2):
w1,w2,theta=0.5,0.5,0.7
tmp = x1*w1 + w2*x2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
print(AND(0,0))
print(AND(1,0))
print(AND(0,1))
print(AND(1,1))

这样就实现了与门
导入权重与偏置
就是数学式中的b为偏置
import numpy as np
x = np.array([0,1])
w = np.array([0.5,0.5])
b = -0.7
print(np.sum(w*x) + b)
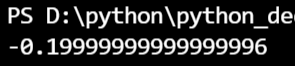
使用权重和配置实现和上面差不多。具体来说,偏置是调整神经元被激活的容易程度的参数。
与非门和或门同理
import numpy as np
def NAND(x1,x2):
x = np.array([x1,x2])
w = np.array([-0.5,-0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
就是设置权重的区别
感知机的局限性
异或门(XOR gate)无法实现,两者相同输出为0,两者不同输出为1
多层感知机
可以通过叠加层来表示异或门
例如通过组合与门,与非门,或门来实现异或门
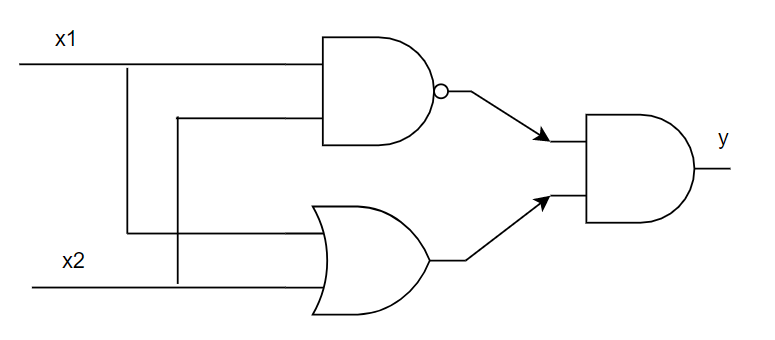
异或门的实现
import numpy as np
def AND(x1,x2): # 与门
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def NAND(x1,x2): # 与非门
x = np.array([x1,x2])
w = np.array([-0.5,-0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1,x2): # 或门
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def XOR(x1,x2):
s1 = NAND(x1,x2)
s2 = OR(x1,x2)
y = AND(s1,s2)
return y
print(XOR(0,0))
从与非门到计算机
仅通过与非门就能实现计算机,感知机通过叠加层能够进行非线性的表示,理论上2层感知机就能构建计算机
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)