【数据结构与算法】详解循环队列：基于数组实现高效存储与访问
【摘要】 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。
目录
一、引言
🍃队列的概念
队列（Queue）是一种常见的数据结构，它遵循先进先出（FIFO）的原则，即最早进入队列的元素将最先被移除。队列在计算机科学中有广泛的应用，比如任务调度、网络流量控制、打印任务管理等。然而，当我们在处理固定大小的空间时，传统的队列实现可能会遇到空间浪费的问题。为了解决这个问题，我们引入了循环队列（Circular Queue）的概念。
关于队列的详细介绍，请参考前置文章
🍃循环队列的概念
循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。相比于传统的队列实现，循环队列能够更有效地利用存储空间，并在数组大小固定的情况下实现队列的无限循环。在本文中，我们将详细探讨如何使用数组来实现循环队列，并分析其优势和应用场景。
🍃为什么使用数组实现循环队列
循环队列的实现方式主要是基于数组的，但也可以采用其他数据结构，如链表。不过，在实际应用中，数组实现循环队列的方式更为常见和高效。
基于数组实现循环队列的特点和优势：
- 空间利用率高：通过将数组的最后一个位置与第一个位置相连，循环队列能够充分利用数组的存储空间，避免传统队列在多次入队和出队操作后可能出现的空间浪费现象。
- 操作简便：在数组实现中，可以通过简单的数学运算（如取模运算）来更新头指针和尾指针，实现入队和出队操作。这使得循环队列的操作非常简便和高效。
- 时间复杂度低：无论是入队还是出队操作，循环队列的时间复杂度都是O(1)，即常数时间复杂度。这意味着无论队列中有多少元素，入队和出队操作所需的时间都是固定的。
循环队列在逻辑上的结构是这样的
但在物理上的结构是这样的
二、循环队列的结构定义
包含
- 指向数组的指针，这是循环队列的底层结构
- 指向队首和队尾的整型变量front和rear
- 循环队列的空间大小k
typedef int CQueueDataType;
typedef struct MyCircularQueue//循环队列结构定义
{
CQueueDataType* a;
int front;
int rear;
int k;
} MyCircularQueue;
三、循环队列的接口实现
🍃队列初始化
- 动态开辟一块循环队列结构体大小的空间
- 为数组指针的指向地址分配一块动态申请的内存，大小为k+1个空间，但实际使用k个（不申请k个是为了区别队列空和队列满，保留一个空间）
- front和rear初始为0（要注意rear初始为0，意味着指向的是队尾的下一个元素）
- k初始化为输入的值
- 最后返回该队列的地址
MyCircularQueue* myCircularQueueCreate(int k) //循环队列初始化
{
MyCircularQueue* tmp = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
tmp->a = (CQueueDataType*)malloc(sizeof(CQueueDataType) * (k + 1));
tmp->front = tmp->rear = 0;
tmp->k = k;
return tmp;
}
🍃入队列
- 首先对形参接收的地址判空
- 然后判断队列是否满
- 如果有空间可用的话，在rear指向的位置插入数据
- 调整rear的位置，向后移动注意考虑循环的问题（rear+1）%（k+1），先对rear+1再对数组长度取模
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) //入队列
{
assert(obj);
if (myCircularQueueIsFull(obj))
return false;
obj->a[obj->rear] = value;
obj->rear = (obj->rear + 1) % (obj->k + 1);
return true;
}
🍃出队列
- 首先对形参接收的地址判空
- 然后判断队列是否为空
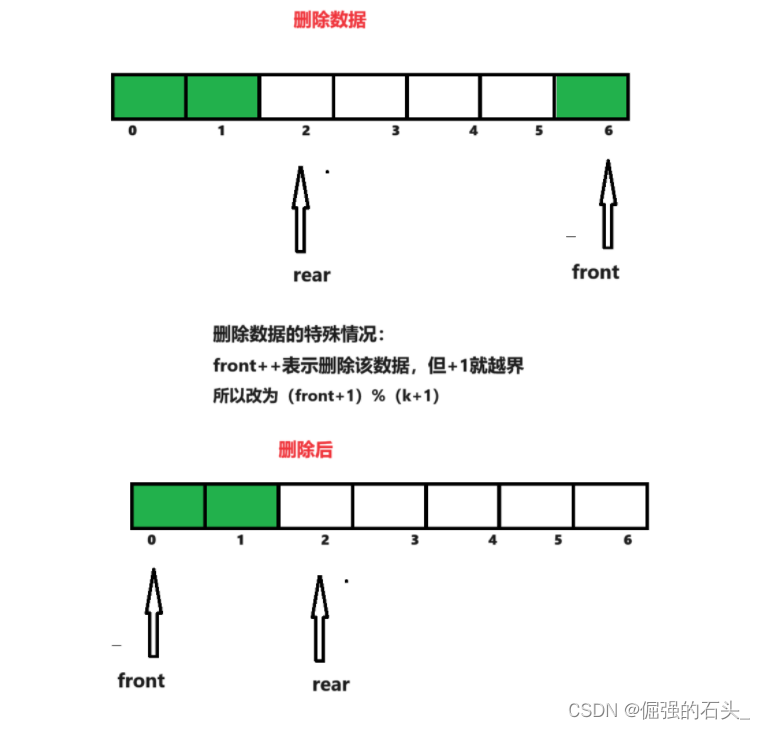
- 如果有数据可出的话，直接调整front的位置即可（不过应当考虑循环值溢出的问题）（front+1)%（k+1）
- 先对front+1再对数组长度取模
bool myCircularQueueDeQueue(MyCircularQueue* obj) //出队列
{
assert(obj);
if (myCircularQueueIsEmpty(obj))
return false;
obj->front = (obj->front + 1) % (obj->k + 1);
return true;
}
🍃取队首元素
- 首先对形参接收的地址判空
- 然后判断队列是否为空（空队列无数据可取）
- 然后返回front位置的元素即可
int myCircularQueueFront(MyCircularQueue* obj) //取队首元素
{
assert(obj);
if (myCircularQueueIsEmpty(obj))
return -1;
return obj->a[obj->front];
}
🍃取队尾元素
- 首先对形参接收的地址判空
- 然后判断队列是否为空（空队列无数据可取）
- 队尾元素是rear位置的前一个元素，考虑到直接-1可能会出错，正确的位置应该是（rear - 1 + k + 1) % (k + 1)，也可以简化成（rear +k ) % (k + 1)
- 返回该位置数据即可
int myCircularQueueRear(MyCircularQueue* obj) //取队尾元素
{
assert(obj);
if (myCircularQueueIsEmpty(obj))
return -1;
return obj->a[(obj->rear - 1 + obj->k + 1) % (obj->k + 1)];
}
🍃判空
- 对形参接收的地址判空
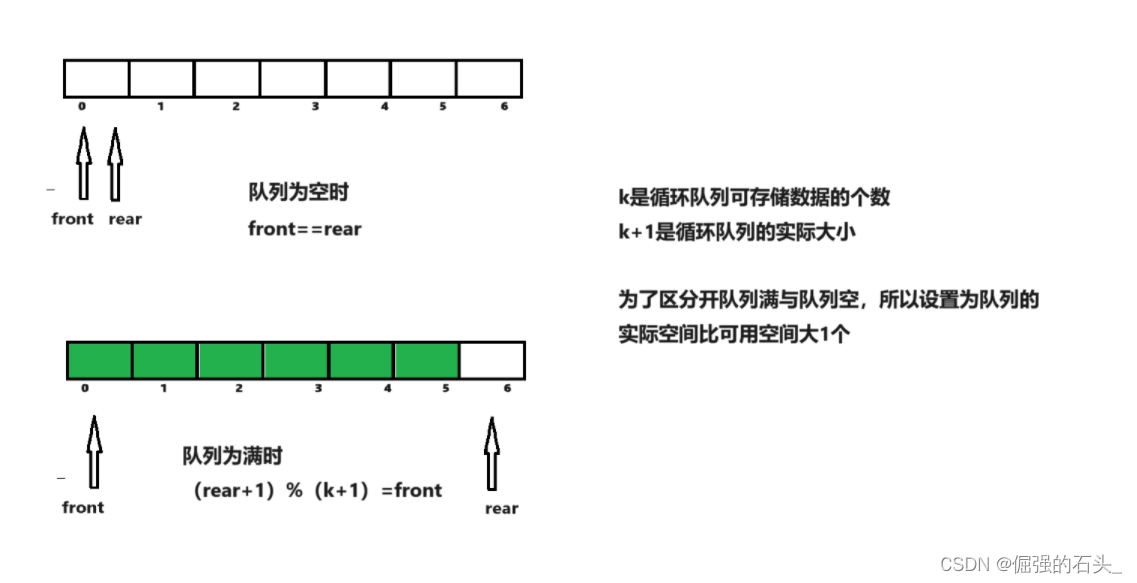
- 然后返回front==rear的结果
bool myCircularQueueIsEmpty(MyCircularQueue* obj) //判空
{
assert(obj);
return obj->front == obj->rear;
}
🍃判满
- 对形参接收的地址判空
- 队列满的条件理应是rear+1==front，但考虑到队列是一个"环形"的，要考虑值的溢出，所以改为（rear + 1 )% （k +1)==front
bool myCircularQueueIsFull(MyCircularQueue* obj) //判满
{
assert(obj);
return (obj->rear + 1) % (obj->k + 1)==(obj->front);
}
🍃队列销毁
- 对形参接收的地址判空
- 然后释放动态申请的数组的空间
- front、rear、k都重置为0
- 最后释放循环队列结构体的空间
void myCircularQueueFree(MyCircularQueue* obj) //循环队列销毁
{
free(obj->a);
obj->front = obj->rear = 0;
obj->k = 0;
free(obj);
obj = NULL;
}
四、C语言实现代码
🍃Circular_Queue.h //循环队列头文件
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int CQueueDataType;
typedef struct MyCircularQueue//循环队列结构定义
{
CQueueDataType* a;
int front;
int rear;
int k;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k); //循环队列初始化
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value);//入队列
bool myCircularQueueDeQueue(MyCircularQueue* obj);//出队列
int myCircularQueueFront(MyCircularQueue* obj);//取队首元素
int myCircularQueueRear(MyCircularQueue* obj); //取队尾元素
bool myCircularQueueIsEmpty(MyCircularQueue* obj); //判空
bool myCircularQueueIsFull(MyCircularQueue* obj);//判满
void myCircularQueueFree(MyCircularQueue* obj); //循环队列销毁
🍃Circular_Queue.c //循环队列源文件
#include"Circular_Queue.h"
MyCircularQueue* myCircularQueueCreate(int k) //循环队列初始化
{
MyCircularQueue* tmp = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
tmp->a = (CQueueDataType*)malloc(sizeof(CQueueDataType) * (k + 1));
tmp->front = tmp->rear = 0;
tmp->k = k;
return tmp;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) //入队列
{
assert(obj);
if (myCircularQueueIsFull(obj))
return false;
obj->a[obj->rear] = value;
obj->rear = (obj->rear + 1) % (obj->k + 1);
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) //出队列
{
assert(obj);
if (myCircularQueueIsEmpty(obj))
return false;
obj->front = (obj->front + 1) % (obj->k + 1);
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) //取队首元素
{
assert(obj);
if (myCircularQueueIsEmpty(obj))
return -1;
return obj->a[obj->front];
}
int myCircularQueueRear(MyCircularQueue* obj) //取队尾元素
{
assert(obj);
if (myCircularQueueIsEmpty(obj))
return -1;
return obj->a[(obj->rear - 1 + obj->k + 1) % (obj->k + 1)];
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) //判空
{
assert(obj);
return obj->front == obj->rear;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) //判满
{
assert(obj);
return (obj->rear + 1) % (obj->k + 1)==(obj->front);
}
void myCircularQueueFree(MyCircularQueue* obj) //循环队列销毁
{
free(obj->a);
obj->front = obj->rear = 0;
obj->k = 0;
free(obj);
obj = NULL;
}
🍃test.c //main函数测试文件
#include"Circular_Queue.h"
void test1()
{
int k = 0;
scanf("%d", &k);
MyCircularQueue* CQ = myCircularQueueCreate(k);//创建循环队列并初始化
if (myCircularQueueIsEmpty(CQ))
printf("队列空\n");
myCircularQueueEnQueue(CQ, 1);//插入五个数据
myCircularQueueEnQueue(CQ, 2);
myCircularQueueEnQueue(CQ, 3);
myCircularQueueEnQueue(CQ, 4);
myCircularQueueEnQueue(CQ, 5);
if (myCircularQueueIsEmpty(CQ))
printf("队列空\n");
else
printf("队列非空\n");
if (myCircularQueueIsFull(CQ))
printf("队列满\n");
else
printf("队列非满\n");
printf("队首元素：%d\n", myCircularQueueFront(CQ));
printf("队尾元素：%d\n", myCircularQueueRear(CQ));
while (!myCircularQueueIsEmpty(CQ))//依次打印队首元素并删除
{
printf("%d ", myCircularQueueFront(CQ));
myCircularQueueDeQueue(CQ);
}
printf("\n");
myCircularQueueFree(CQ);
}
int main()
{
test1();
return 0;
}
测试结果
五、循环队列的应用场景
循环队列在实际应用中有着广泛的用途。以下是一些常见的应用场景：
任务调度：在操作系统中，任务调度器通常使用队列来管理待执行的任务。循环队列可以有效地处理这些任务，确保它们按照先进先出的顺序被执行。由于操作系统的资源有限，使用循环队列可以最大化地利用这些资源，避免不必要的空间浪费。
网络通信：在网络通信中，数据包经常需要在不同的节点之间传输。循环队列可以用于在节点上管理这些数据包，确保它们按照正确的顺序被发送和接收。特别是在路由器和交换机等网络设备中，循环队列可以有效地处理大量的数据包，提高网络性能。
打印机管理：在打印系统中，多个打印任务可能需要同时发送到打印机。循环队列可以用于管理这些打印任务，确保它们按照接收的顺序被打印出来。使用循环队列可以避免打印任务的混乱和丢失，提高打印效率。
模拟系统：在模拟系统中，如模拟银行排队系统或模拟医院挂号系统等，循环队列可以模拟现实中的排队情况。通过循环队列的入队和出队操作，可以模拟客户的到来和离开，以及服务员的接待过程。这有助于分析系统的性能和瓶颈，优化服务流程。
六、总结
循环队列是一种利用数组循环特性实现队列操作的数据结构。它通过维护头指针和尾指针来管理队列的入队和出队操作，实现了对固定大小空间的高效利用。
循环队列在任务调度、网络通信、打印机管理以及模拟系统等多个领域都有广泛的应用。
通过本文的介绍和分析，我们可以看到循环队列在解决实际问题时具有显著的优势和灵活性。因此，掌握循环队列的实现原理和应用方法对于提高编程能力和解决实际问题具有重要意义。
【版权声明】本文为华为云社区用户原创内容，未经允许不得转载，如需转载请自行联系原作者进行授权。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）