@TOC

概述

通过前面的内容，我们深入剖析了单个感知机是如何运作的，如果想了解欢迎考古：感知机从理论到代码。
接下里，我们来探讨一下：
为什么感知机不能解决疑惑问题，但是多层感知机却可以解决？
为什么激活函数从分段函数变成了sigmoid函数？

异或问题

前置

我们知道计算机的所有程序最底层都是由与、或、异或来组成的，假设我们证明了多层感知机可以实现这四种运算，那么我们就可以假设它理论上可以逼近任何函数。

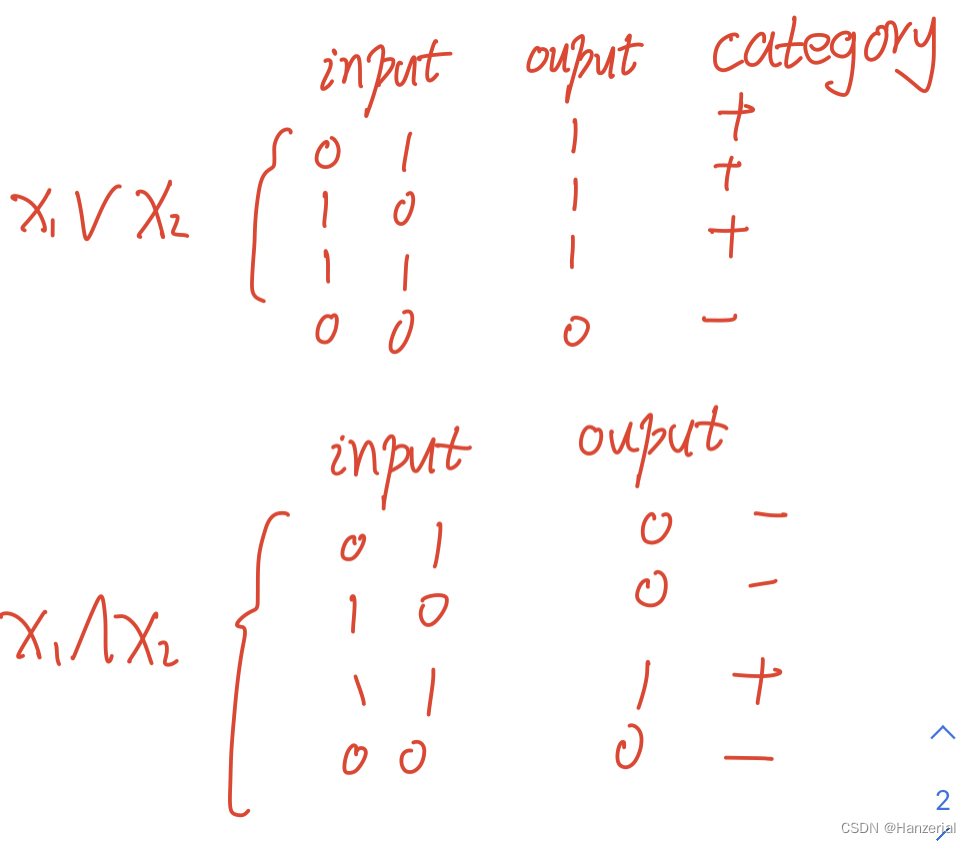
感知机模型公式为：

$$\begin{aligned}z=\sum ^{n}_{i=1}\left( w_{i}x_{i}\right) +b\\ f\left( z\right) \begin{cases}z\geq 0\\ z <-1\end{cases}\end{aligned}$$

下面介绍一下感知机如何实现与或非运算。

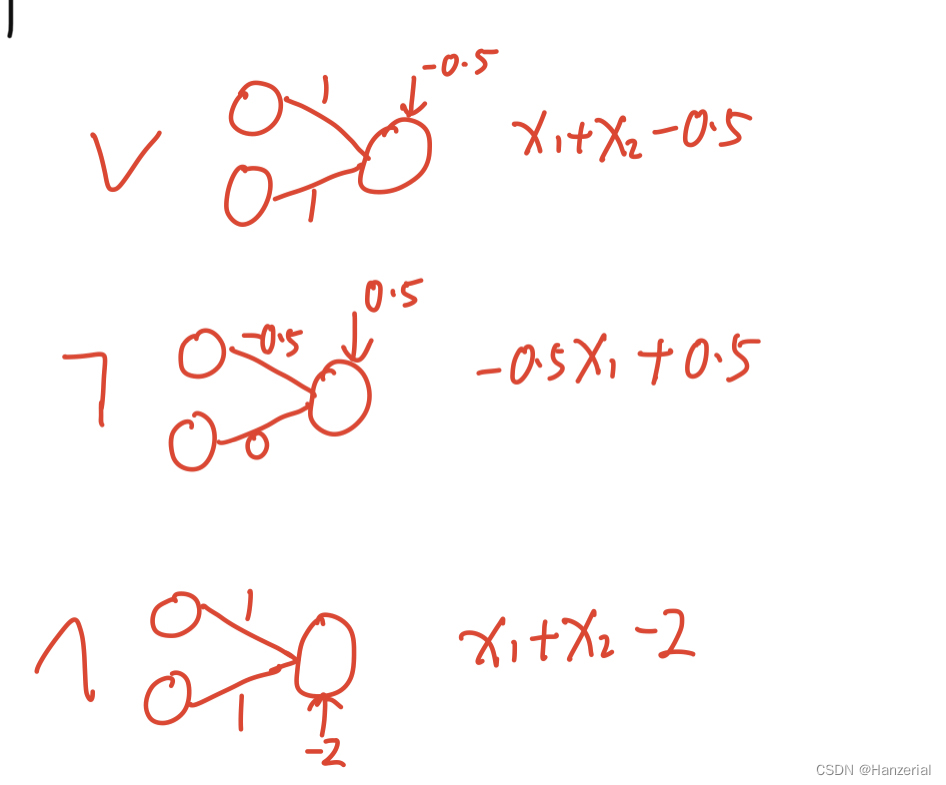
从公式角度理解

异或表达式： $x\bigoplus y=(x\bigwedge \overline y) \bigvee (\overline x\bigwedge y)$
从表达式我们看出，异或运算是通过三个基本运算的组合而成的，我们之前说过一个感知机可以实现三种基本运算，那么我们是不是也可以用感知机的叠加来表达疑惑操作呢？
从疑惑表达式我们发现，它是由两个与运算的组成的或运算，我们把它分成两部分：
公式1: $(x\bigwedge \overline y)$
公式2: $(\overline x\bigwedge y)$
我们用一个感知机实现公式1，用另一个感知机实现公式2，然后我们这两个感知机的输出作为公式实现或运算感知机的输入，那么最终感知机的输出，也就是疑惑运算的结果。如图所示：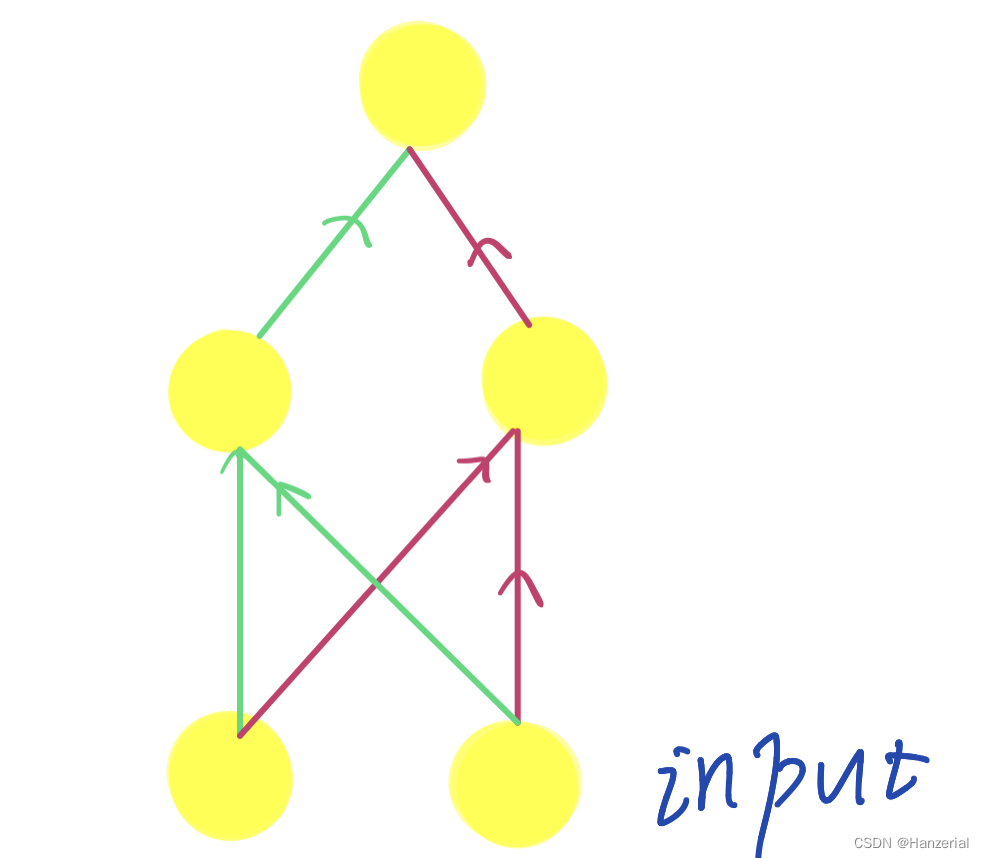

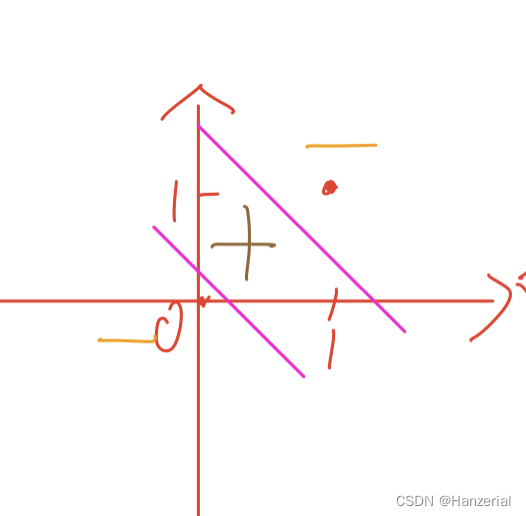
从图像角度解释：

单个感知机他实际上是一个线性函数（也就是一条直线），
基础运算如图所示：

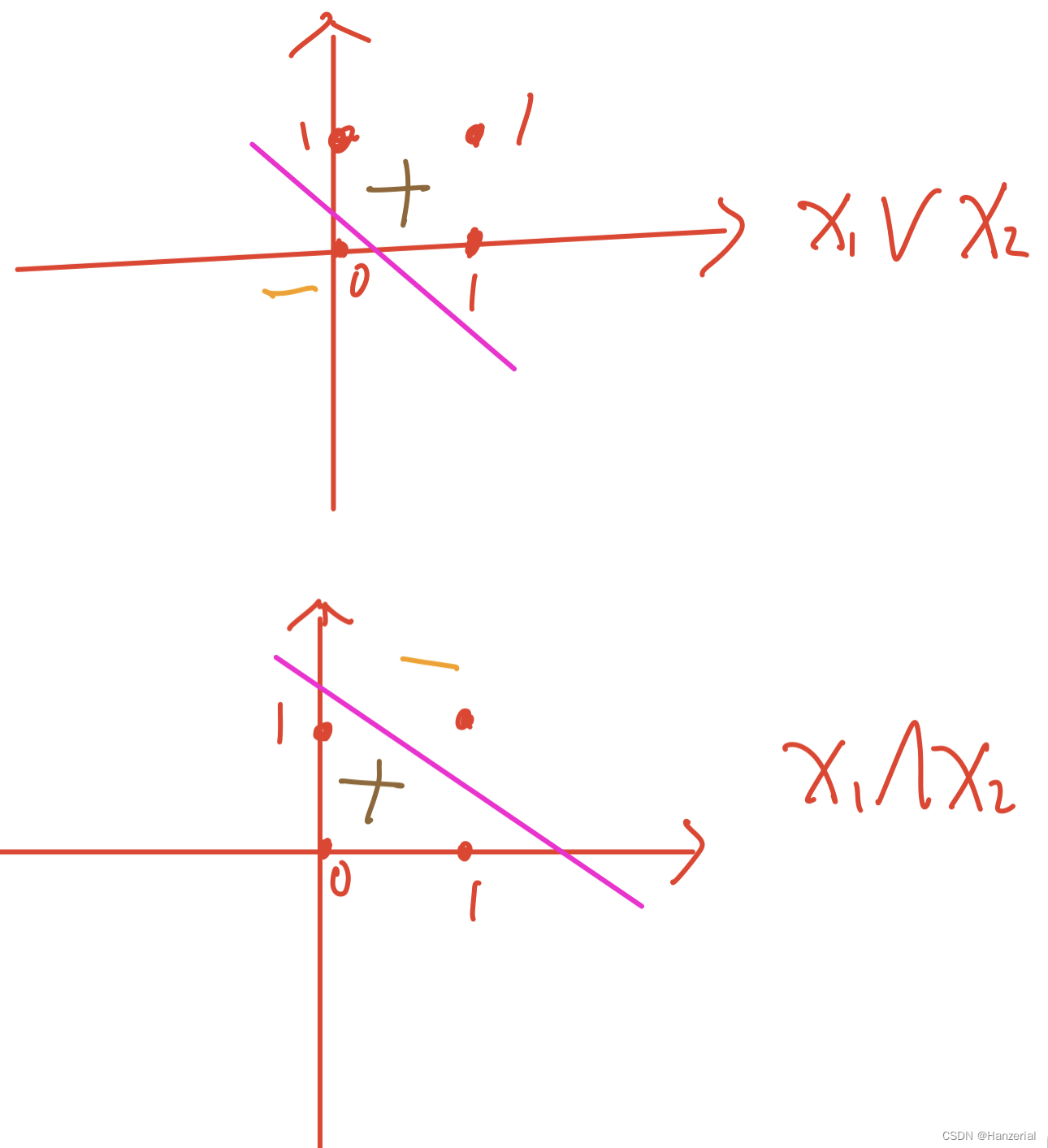
然后对着两个图像做或运算，可大致变为：

激活函数

在最开始我们的激活函数采用分段函数，但是它具有不光滑、不连续的等不太好的性质，不方便我们后续工作，所以通常我们把激活函数换成了sigmoid函数，他可以把函数挤压在（0，1）之间，因此也称作挤压函数。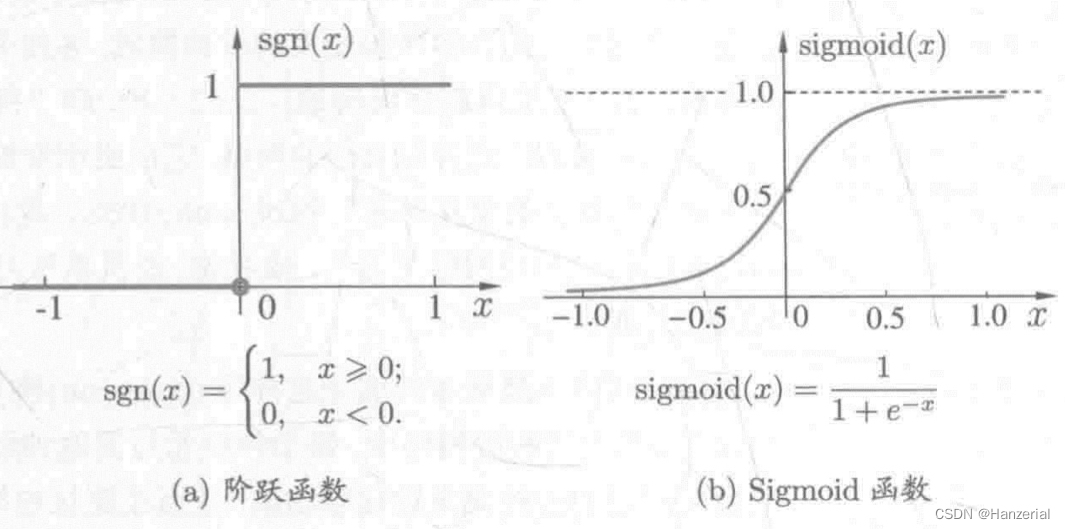

代码

import torch.nn as nn
import torch.nn.functional as F


# 异或门模块由两个全连接层构成
class XORModule(nn.Module):
    def __init__(self):
        super(XORModule, self).__init__()
        self.fc1 = nn.Linear(2, 2)
        self.fc2 = nn.Linear(2, 1)
        self.relu = nn.ReLU()

    def forward(self, x):
        x = x.view(-1, 2)
        x = self.relu((self.fc1(x)))
        x = self.fc2(x)
        return x