异常检测的原理是基于正态分布的概率密度函数得出，检验概率是否为小概率时间
此次使用的为正态分布为标准正态分布和相关性正态分布（特征变量之间可能有相关性）
数据的异常需要标注，需要有监督学习

1 正确率检验

分布使用正确率和召回率进行检验 (2.0precisionrecall)/(precision+recall)

def F1(predictions,y):
    TP=np.sum((predictions==1)&(y==1))
    FP=np.sum((predictions==1)&(y==0))
    FN=np.sum((predictions==0)&(y==1))
    if (TP+FP)==0:
        precision=0
    else:
        precision=float(TP)/(TP+FP)
    if (TP+FN)==0:
        recall=0
    else:
        recall=float(TP)/(TP+FN)
    if precision+recall==0:
        return 0
    else:
        return (2.0*precision*recall)/(precision+recall)

2 普通正态分布概率密度函数

def gaussianModel(X):
    #参数估计
    m,n=X.shape
    mu=np.mean(X,axis=0)
    sigma2=np.var(X,axis=0)
    
    def p(x):#x是单个样本，n*1维
        total=1
        for j in range(x.shape[0]):
            total*=np.exp(-np.power((x[j,0]-mu[0,j]),2)/(2*sigma2[0,j]))/(np.sqrt(2*np.pi*sigma2[0,j]))
        return total
    return p

3 相关正态分布概率密度函数

特征变量之间可能存在相关性

def multivariateGaussianModel(X):
    #参数估计
    m,n=X.shape
    mu=np.mean(X.T,axis=1)
    sigma=np.mat(np.cov(X.T))
    detSigma=np.linalg.det(sigma)
    
    def p(x):
        x=x-mu
        return np.exp(-x.T*np.linalg.pinv(sigma)*x/2).A[0]*((2*np.pi)**(-n/2.0)*(detSigma**(-0.5)))
    return p

4 模型选择于epsilon残差选择

def train(X,model=gaussianModel):
return model(X) #返回的是概率模型p

def selectEpsilon(XVal,yVal,p):
    pVal=np.mat([p(x.T) for x in XVal]).reshape(-1,1)#交叉验证集中所有样本的概率
    step=(np.max(pVal)-np.min(pVal))/1000.0
    
    bestEpsilon=0
    bestF1=0
    
    for epsilon in np.arange(np.min(pVal),np.max(pVal),step):
        predictions=pVal<epsilon
        f1=F1(predictions,yVal)
        if f1>bestF1:
            bestF1=f1
            bestEpsilon=epsilon
    return bestEpsilon,bestF1

返回残差选择值能使F1最大的值

5 读取数据准备

%matplotlib inline
from scipy.io import loadmat
import matplotlib.pyplot as pl
pl.rcParams[‘font.sans-serif’]=‘SimHei’ #画图正常显示中文
pl.rcParams[‘axes.unicode_minus’]=False #决绝保存图像是负号‘-’显示方块的问题

def loadDataset(filename):
    X=[]
    Y=[]
    with open(filename,'rb') as f:
        for idx,line in enumerate(f):
            line=line.decode('utf-8').strip()
            if not line:
                continue
                
            eles=line.split(',')
            
            if idx==0:
                numFea=len(eles)
                
            eles=list(map(float,eles))#map返回一个迭代对象
            
            X.append(eles[:-1])
            Y.append([eles[-1]])
    return np.array(X),np.array(Y)

#低维数据测试
ori_X,ori_y=loadDataset(’./data/gender_predict.csv’)
m,n=ori_X.shape

X=np.mat(ori_X[40:100])
y=np.mat(ori_y[40:100])
XVal=np.mat(ori_X[20:40])
yVal=np.mat(ori_y[20:40])
Xtest=np.mat(ori_X[0:20])
ytest=np.mat(ori_y[0:20])

6 检验绘图

p=train(X)
#p=train(X,model=multivariateGaussianModel)

pTest=np.mat([p(x.T) for x in X]).reshape(-1,1)
#绘制数据点
pl.xlabel(u'年龄')
pl.ylabel(u'收入')
pl.plot(X[:,0],X[:,1],'bx')
epsilon,f1=selectEpsilon(XVal,yVal,p)

print(u'基于交叉验证集最佳ε: %e\n'%epsilon)
print(u'基于交叉验证集最佳F1: %f\n'%f1)
print(u'找到%d个异常点'%np.sum(pTest<epsilon))

#获得训练集的异常点
outliers=np.where(pTest<epsilon,True,False).ravel()
pl.plot(X[outliers,0],X[outliers,1],'ro',lw=2,markersize=10,fillstyle='none',markeredgewidth=1)
n=np.linspace(0,60,100)
X1=np.meshgrid(n,n)
XFit=np.mat(np.column_stack((X1[0].T.flatten(),X1[1].T.flatten())))
pFit=np.mat([p(x.T) for x in XFit]).reshape(-1,1)
pFit=pFit.reshape(X1[0].shape)

if not np.isinf(np.sum(pFit)):
    pl.contour(X1[1],X1[0],pFit,10.0**np.arange(-6,0,3).T)
pl.show()

使用交叉验证集选择的超惨epsilon进行异常值检验，绘图标注训练集

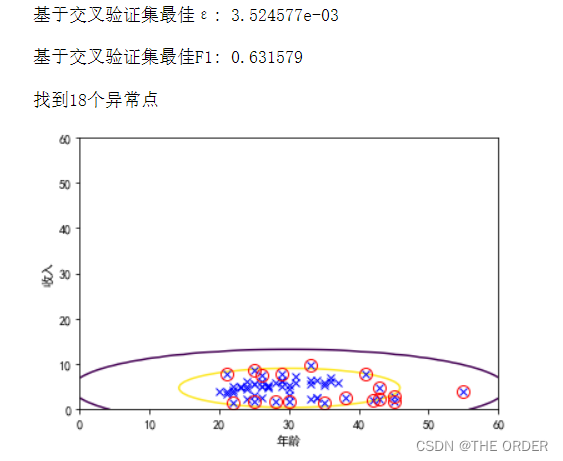
发现较好的把数据进行了检测

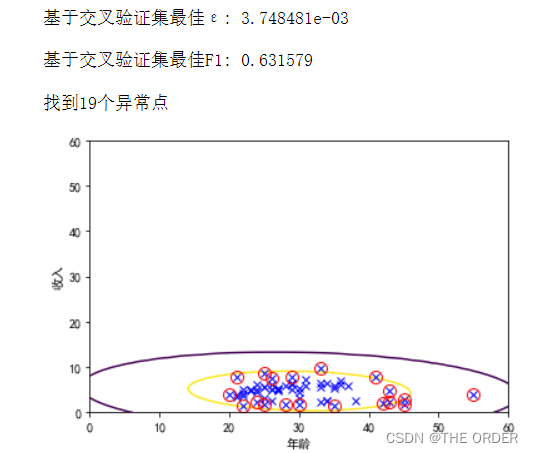
7 使用有相关性的检验

只改了第一行的代码，将p使用的模型进行了更改

#p=train(X)
p=train(X,model=multivariateGaussianModel)

pTest=np.mat([p(x.T) for x in X]).reshape(-1,1)
#绘制数据点
pl.xlabel(u'年龄')
pl.ylabel(u'收入')
pl.plot(X[:,0],X[:,1],'bx')
epsilon,f1=selectEpsilon(XVal,yVal,p)

print(u'基于交叉验证集最佳ε: %e\n'%epsilon)
print(u'基于交叉验证集最佳F1: %f\n'%f1)
print(u'找到%d个异常点'%np.sum(pTest<epsilon))

#获得训练集的异常点
outliers=np.where(pTest<epsilon,True,False).ravel()
pl.plot(X[outliers,0],X[outliers,1],'ro',lw=2,markersize=10,fillstyle='none',markeredgewidth=1)
n=np.linspace(0,60,100)
X1=np.meshgrid(n,n)
XFit=np.mat(np.column_stack((X1[0].T.flatten(),X1[1].T.flatten())))
pFit=np.mat([p(x.T) for x in XFit]).reshape(-1,1)
pFit=pFit.reshape(X1[0].shape)

if not np.isinf(np.sum(pFit)):
    pl.contour(X1[1],X1[0],pFit,10.0**np.arange(-6,0,3).T)
pl.show()