【 数据结构】栈和队列:从基础到实战
在编程里,栈和队列是两种超常用的“数据容器”,就像日常生活里的“收纳盒”,只不过它们有自己的“取用规则”。今天咱们就从基础用法到实际刷题,一步步把这俩概念讲明白,再聊聊它们背后的实现逻辑。
一、栈(Stack):先进后出的“叠盘子”
栈的核心特点就一个——先进后出(First In Last Out,简称FILO)。打个比方:你把盘子一个叠一个放桌上,先放的盘子在最底下,最后放的在最上面;拿的时候只能从最上面开始拿,先放的反而最后才能拿到,这就是栈的逻辑。
如图所示,栈的元素只能从“栈顶”进出,栈底是碰不到的:

1. 怎么定义一个栈?
栈在C++里不是“自己存数据”,而是“借别人的容器当仓库”(这个“借”的逻辑叫“容器适配器”,后面会讲)。默认情况下,它借的是deque容器,也可以指定借vector或list。
两种定义方式:
// 方式一:用默认底层容器(deque)定义栈,存int类型数据
stack<int> st1;
// 方式二:指定底层容器(vector/list)
stack<int, vector<int>> st2; // 用vector当仓库
stack<int, list<int>> st3; // 用list当仓库
2. 栈的常用操作
栈的操作很简单,就围绕“栈顶”做文章,常用的就5个函数,一看就懂:
| 成员函数 | 功能说明 | 通俗理解 |
|---|---|---|
| empty() | 判断栈是否为空 | 看盘子叠里有没有盘子 |
| size() | 求栈里元素的个数 | 数盘子有几个 |
| top() | 获取栈顶元素(不删除) | 看最上面那个盘子是什么 |
| push(x) | 把x放到栈顶 | 往盘子叠上再放一个 |
| pop() | 删除栈顶元素(不返回) | 把最上面的盘子拿走 |
| swap(s) | 交换两个栈的所有元素 | 把两叠盘子互换 |
3. 代码示例:用栈实现“叠盘子”
咱们写段代码,模拟“放4个盘子(1、2、3、4),再从顶往下拿”的过程:
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
int main() {
// 定义一个用vector当底层的栈,存int
stack<int, vector<int>> st;
// 往栈里放元素(叠盘子:1在最下,4在最上)
st.push(1);
st.push(2);
st.push(3);
st.push(4);
// 看栈里有几个元素(输出4)
cout << "栈里元素个数:" << st.size() << endl;
// 从栈顶往下拿,直到栈空
while (!st.empty()) { // 先判断栈是不是空的
cout << st.top() << " "; // 看栈顶元素
st.pop(); // 拿走栈顶元素
}
cout << endl; // 输出结果:4 3 2 1(先进后出)
return 0;
}
运行后会发现,输出是4 3 2 1,正好对应“先放的1最后拿,后放的4最先拿”,完美体现栈的“先进后出”。
二、队列(Queue):先进先出的“排队”
队列和栈正好相反,核心特点是先进先出(First In First Out,简称FIFO)。就像日常生活里排队买奶茶:先排队的人先买,后排队的人后买,没人会插队(队列也不允许中间操作)。
如图所示,队列只能从“队尾”加元素,从“队头”删元素,中间的元素碰不到:
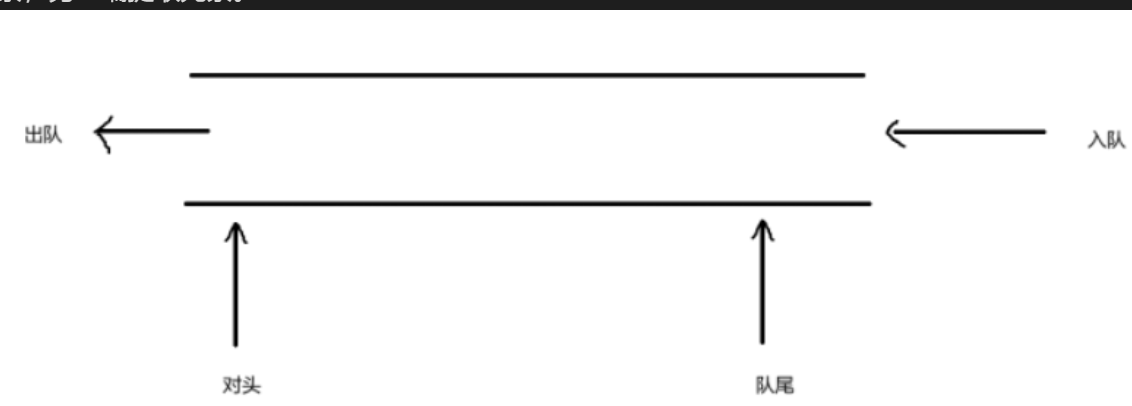
1. 怎么定义一个队列?
和栈一样,队列也是“容器适配器”,默认借deque当底层容器,也能指定vector或list(但vector头删慢,一般不用它当队列底层)。
定义方式和栈几乎一样:
// 方式一:默认底层容器(deque),存int
queue<int> q1;
// 方式二:指定底层容器
queue<int, vector<int>> q2; // 用vector(不推荐,头删慢)
queue<int, list<int>> q3; // 用list(推荐,两头操作快)
2. 队列的常用操作
队列的操作围绕“队头”和“队尾”,比栈多了个“看队尾”的函数:
| 成员函数 | 功能说明 | 通俗理解 |
|---|---|---|
| empty() | 判断队列是否为空 | 看队伍里有没有人 |
| size() | 求队列元素个数 | 数队伍有几个人 |
| front() | 获取队头元素(不删除) | 看队伍最前面的人 |
| back() | 获取队尾元素(不删除) | 看队伍最后面的人 |
| push(x) | 把x放到队尾 | 新的人排到队伍最后 |
| pop() | 删除队头元素(不返回) | 最前面的人买完走了 |
| swap(q) | 交换两个队列的元素 | 两排队伍互换 |
3. 代码示例:用队列模拟“排队买奶茶”
咱们写段代码,模拟“4个人(1、2、3、4)排队,先排的先买”:
#include <iostream>
#include <queue>
#include <list>
using namespace std;
int main() {
// 定义一个用list当底层的队列,存int
queue<int, list<int>> q;
// 往队尾加元素(排队:1在队头,4在队尾)
q.push(1);
q.push(2);
q.push(3);
q.push(4);
// 看队列里有几个人(输出4)
cout << "队列里元素个数:" << q.size() << endl;
// 从队头开始“买奶茶”,直到队空
while (!q.empty()) {
cout << q.front() << " "; // 看队头的人
q.pop(); // 队头的人走了
}
cout << endl; // 输出结果:1 2 3 4(先进先出)
return 0;
}
运行后输出1 2 3 4,和排队逻辑完全一致——先排的1先“买”,后排的4最后“买”,这就是队列的“先进先出”。
三、中缀表达式与后缀表达式:机器更喜欢哪种?
咱们平时写的数学表达式,比如1 + 2 * 3,叫“中缀表达式”——操作符(+、*)夹在两个操作数中间。但中缀表达式有个麻烦:要考虑优先级(先算乘法再算加法),机器处理起来不方便。
于是就有了“后缀表达式”(也叫逆波兰表达式):把操作符放到两个操作数后面,比如1 2 3 * +。它的规则特别简单:操作数、操作数、操作符,完全不用考虑优先级,机器用栈一推就出结果。
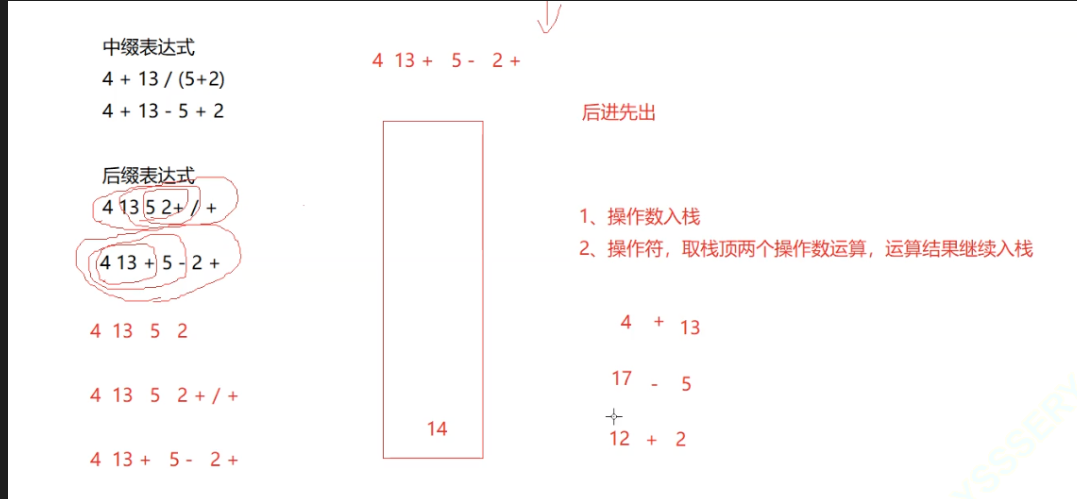
两种表达式的对比,如图所示:

后缀表达式的计算过程也很直观,还是用栈:遇到操作数就入栈,遇到操作符就把栈顶两个操作数拿出来算,结果再入栈。比如算1 2 3 * +:
- 1、2、3依次入栈;
- 遇到
*,把3(栈顶,右操作数)和2(左操作数)拿出来,算2*3=6,6入栈; - 遇到
+,把6(右操作数)和1(左操作数)拿出来,算1+6=7,7入栈; - 最后栈里只剩7,就是结果。
整个过程如图所示,一步一步很清晰:

四、实战:逆波兰表达式求值(LeetCode 150题)
理解了后缀表达式的计算逻辑,咱们直接看一道LeetCode经典题:逆波兰表达式求值。题目给一个字符串数组(比如["2","1","+","3","*"]),求它的结果(这里结果是(2+1)*3=9)。
1. 解题思路
核心就是用栈,步骤和刚才讲的后缀计算完全一样:
- 定义一个栈,用来存操作数;
- 遍历字符串数组:
- 如果是数字(比如"2"),转成int入栈;
- 如果是操作符(+、-、*、/),就把栈顶两个数拿出来(注意:先拿的是右操作数,后拿的是左操作数),计算后把结果入栈;
- 遍历结束后,栈里只剩一个数,就是答案。
思路图示如下,一看就懂:
2. 代码实现
#include <iostream>
#include <vector>
#include <stack>
#include <string>
using namespace std;
class Solution {
public:
int evalRPN(vector<string>& tokens) {
// 1. 定义一个栈,存操作数
stack<int> st;
// 2. 遍历每个字符串
for (auto& str : tokens) {
// 判断是不是操作符(+、-、*、/)
if (str == "+" || str == "-" || str == "*" || str == "/") {
// 先拿右操作数(栈顶是后入的,比如"2 1 +",1是右,2是左)
int right = st.top();
st.pop(); // 拿走右操作数
// 再拿左操作数
int left = st.top();
st.pop(); // 拿走左操作数
// 根据操作符计算,结果入栈
switch (str[0]) { // str是字符串,取第一个字符判断
case '+':
st.push(left + right);
break;
case '-':
st.push(left - right); // 注意:左减右,不能反
break;
case '*':
st.push(left * right);
break;
case '/':
st.push(left / right); // 左除右,注意整数除法
break;
}
} else {
// 不是操作符,就是数字,转成int入栈
st.push(stoi(str)); // stoi:字符串转int
}
}
// 最后栈里只剩一个数,就是结果
return st.top();
}
};
// 测试代码
int main() {
Solution sol;
// 测试用例:["2","1","+","3","*"] → (2+1)*3=9
vector<string> tokens = {"2","1","+","3","*"};
cout << "结果:" << sol.evalRPN(tokens) << endl; // 输出9
return 0;
}
这里要注意一个细节:拿操作数时,必须先拿“右操作数”,再拿“左操作数”。比如算2-1,后缀表达式是2 1 -,栈里先放2再放1,遇到-时,先拿1(右),再拿2(左),算2-1才对,反了就成1-2了,结果会错。
五、底层揭秘:栈和队列都是“容器适配器”
前面一直说栈和队列是“容器适配器”,到底什么是“适配器”?简单说:适配器不是“新容器”,而是“包装器” ——它自己不实现“存数据”的功能,而是把别的容器(比如deque、vector、list)包装一下,只暴露自己需要的接口(比如栈只暴露栈顶操作,队列只暴露队头队尾操作)。
就像你买了一个“多功能工具箱”,但你只需要用它的“螺丝刀”功能,于是你加了个“盖子”,只露出螺丝刀——这个“盖子”就是适配器,工具箱就是底层容器。
如图所示,适配器的核心是“复用底层容器的功能,隐藏不需要的接口”:

为什么默认用deque当底层容器?因为deque有两个优点:
- 尾插、尾删速度快(满足栈的需求);
- 头删、尾插速度快(满足队列的需求);
而vector头删慢(队列用着不方便),list虽然两头快,但内存碎片多(不如deque高效)。所以deque是“万金油”,成了默认选择。
再看栈和队列对底层容器的要求:
- 栈需要的操作:尾插(push_back)、尾删(pop_back)、取尾元素(back)——所以
vector、list、deque都能当栈的底层; - 队列需要的操作:尾插(push_back)、头删(pop_front)、取头元素(front)、取尾元素(back)——
list和deque能满足,vector头删慢,不推荐。
相关的底层逻辑图示,帮你进一步理解:



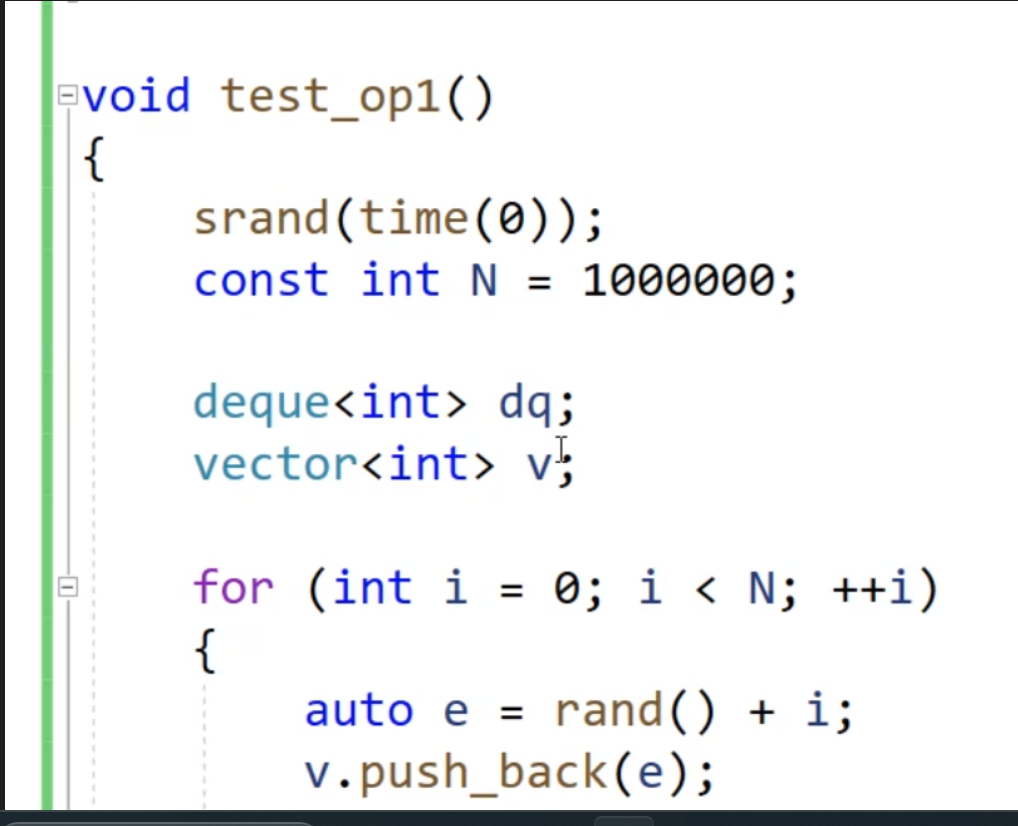
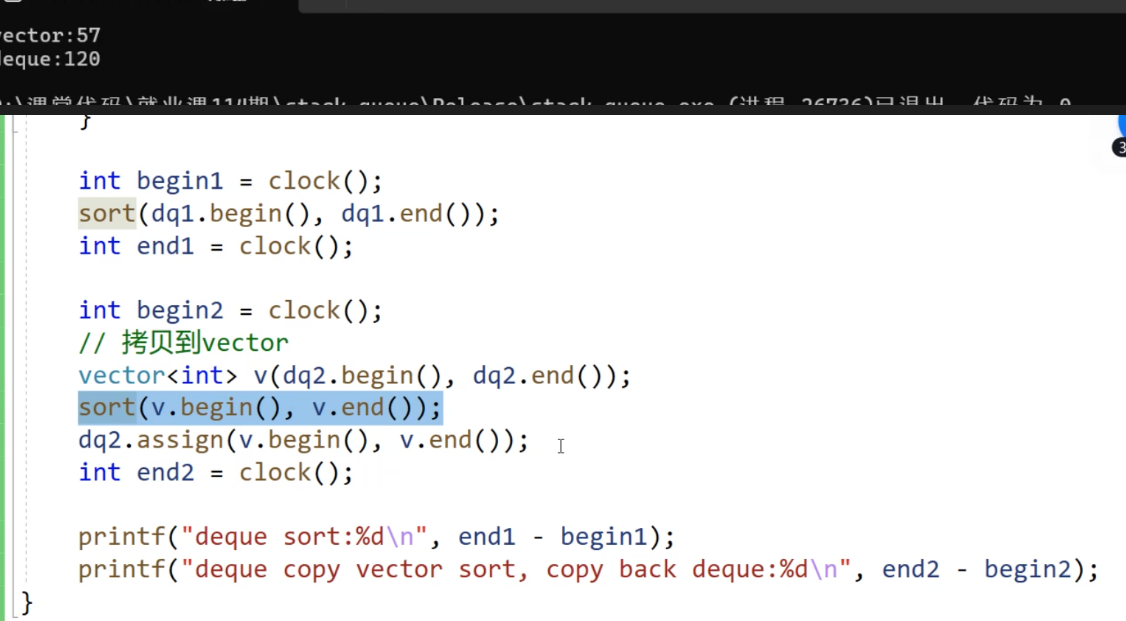
![[Pasted image 20250717113120.png]]



总结
- 栈是“先进后出”的容器,像叠盘子,只能操作栈顶;
- 队列是“先进先出”的容器,像排队,只能操作队头和队尾;
- 后缀表达式(逆波兰)适合机器计算,核心用栈实现;
- 栈和队列都是“容器适配器”,默认借
deque当底层,也能指定其他容器。
这俩数据结构虽然简单,但用途特别广——比如栈能用于函数调用、括号匹配,队列能用于任务调度、BFS算法,掌握它们是学好编程的基础~
- 点赞
- 收藏
- 关注作者


评论(0)