机器学习笔记

一、什么是机器学习？
机器学习=寻找一种函数，如何寻找这个函数？
①定一个函数集合 ②判断函数的好坏 ③选择最好的函数

机器学习三板斧
①设计模型model

②判断模型的好坏

③选择最好的函数，优化模型

    3.1修改模型，增加数据维度

    3.2增加正则因子，使函数更加平滑，让参数w取值更小。（x变化较小时，整个函数结果不会变化太大，结果更准）

学习路线
监督学习：有数据标注情况下学习（回归、分类）

半监督学习：训练数据中带标记的数据不够多

迁移学习：在已学习基础上，做看似和以前学习不相关的事情，但实际效果很好（在猫狗识别基础识别大象老虎等）

非监督学习：没有具体标注数据的情况下学习（机器阅读、机器绘画）

结构化学习：超越简单的回归和分类，产生结构化的结果（如图片、语言、声音）

二、机器学习算法的类型
1. 有监督学习
有监督学习通常是利用带有专家标注的标签的训练数据，学习一个从输入变量X到输入变量Y的函数映射。 Y = f (X)

训练数据通常是(n×x,y)的形式，其中n代表训练样本的大小，x和y分别是变量X和Y的样本值。

利用有监督学习解决的问题大致上可以被分为两类：

分类问题：预测某一样本所属的类别（离散的）。比如给定一个人（从数据的角度来说，是给出一个人的数据结构，包括：身高，年龄，体重等信息），然后判断是性别，或者是否健康。

回归问题：预测某一样本的所对应的实数输出（连续的）。比如预测某一地区人的平均身高。

下面所介绍的前五个算法（线性回归，逻辑回归，分类回归树，朴素贝叶斯，K最近邻算法）均是有监督学习的例子。

除此之外，集成学习也是一种有监督学习。它是将多个不同的相对较弱的机器学习模型的预测组合起来，用来预测新的样本。本文中所介绍的第九个和第十个算法（随机森林装袋法，和XGBoost算法）便是集成技术的例子。

2. 无监督学习
  无监督学习问题处理的是，只有输入变量X没有相应输出变量的训练数据。它利用没有专家标注训练数据，对数据的结构建模。

可以利用无监督学习解决的问题，大致分为两类：

关联分析：发现不同事物之间同时出现的概率。在购物篮分析中被广泛地应用。如果发现买面包的客户有百分之八十的概率买鸡蛋，那么商家就会把鸡蛋和面包放在相邻的货架上。

聚类问题：将相似的样本划分为一个簇（cluster）。与分类问题不同，聚类问题预先并不知道类别，自然训练数据也没有类别的标签。

维度约减：顾名思义，维度约减是指减少数据的维度同时保证不丢失有意义的信息。利用特征提取方法和特征选择方法，可以达到维度约减的效果。特征选择是指选择原始变量的子集。特征提取是将数据从高纬度转换到低纬度。广为熟知的主成分分析算法就是特征提取的方法。

下面介绍的第六-第八（Apriori算法，K-means算法，PCA主成分分析）都属于无监督学习。

3. 强化学习
  通过学习可以获得最大回报的行为，强化学习可以让agent（个体）根据自己当前的状态，来决定下一步采取的动作。

强化学习算法通过反复试验来学习最优的动作。这类算法在机器人学中被广泛应用。在与障碍物碰撞后，机器人通过传感收到负面的反馈从而学会去避免冲突。在视频游戏中，我们可以通过反复试验采用一定的动作，获得更高的分数。Agent能利用回报去理解玩家最优的状态和当前他应该采取的动作。

三、十大机器学习算法介绍
有监督学习
1. 线性回归算法
  在机器学习当中，我们有一个变量X的集合用来决定输出变量Y。在输入变量X和输出变量Y之间存在着某种关系。机器学习的目的就是去量化这种关系。

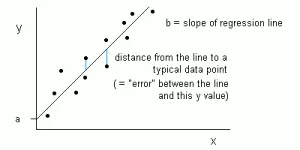
  在线性回归里，输入变量X和输出变量Y之间的关系，用等式Y = a + bX 来表示。因此，线性回归的目标便是找出系数a和b的值。在这里，a是截距，b是斜率。

  上图绘制了数据中X和Y的值。我们的目标是去拟合一条最接近所有点的直线。这意味着，直线上每一个X对应点的Y值与实际数据中点X对应的Y值，误差最小。

2. 逻辑回归算法
  使用一个转换函数后，线性回归预测的是连续的值（比如降雨量），而逻辑回归预测的是离散的值（比如一个学生是否通过考试，是：0，否：1）。

  逻辑回归最适用于二分类（数据只分为两类，Y = 0或1，一般用1作为默认的类。比如：预测一个事件是否发生，事件发生分类为1；预测一个人是否生病，生病分类为1）。我们称呼其为逻辑回归（logistic regression）是因为我们的转换函数采用了logistic function (h(x)=1/(1+e的-x次方)) 。

  在逻辑回归中，我们首先得到的输出是连续的默认类的概率p（0小于等于p小于等于1）。转换函数 (h(x)=1/(1+e的-x次方))的值域便是（0,1）。我们对该函数设置一个域值t。若概率p>t，则预测结果为1。

图 2 使用逻辑回归来判断肿瘤是恶性还是良性。如果概率p大于0.5，则是恶性

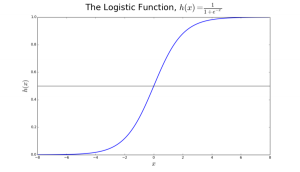
在图2中，判断肿瘤是恶性还是良性。默认类y=1（肿瘤是恶性）。当变量X是测量肿瘤的信息，如肿瘤的尺寸。如图所示，logistic函数由变量X得到输出p。域值t在这里设置为0.5。如果p大于t，那么肿瘤则是恶性。

我们考虑逻辑回归的一种变形：

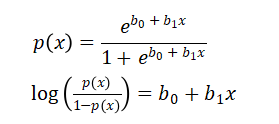
  因此，逻辑回归的目标便是训练数据找到适当的参数的值，使得预测的输出和实际的输出最小。我们使用最大似然估计来对参数进行估计。

3. 分类回归树（决策树）
  分类回归树是诸多决策树模型的一种实现，类似还有ID3、C4.5、CART等算法。

  非终端节点有根节点（Root Node）和内部节点(Internal Node)。终端节点是叶子节点(Leaf Node)。每一个非终端节点代表一个输出变量X和一个分岔点，叶叶子节点代表输出变量Y，见图3。沿着树的分裂（在分岔点做一次决策）到达叶子节点，输出便是当前叶子节点所代表的值。

图3中的决策树，根据一个人的年龄和婚姻状况进行分类：1.购买跑车；2.购买小型货车。如果这个人30岁还没有结婚，我们沿着决策树的过程则是：‘超过30年？–是--已婚？–否，那么我们的输出便是跑车。

4. 朴素贝叶斯

在给定一个事件发生的前提下，计算另外一个事件发生的概率——我们将会使用贝叶斯定理。假设先验知识为d，为了计算我们的假设h为真的概率，我们将要使用如下贝叶斯定理：

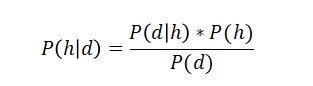
P(h|d)=后验概率。这是在给定数据d的前提下，假设h为真的概率。

P(d|h)=可能性。这是在给定假设h为真的前提下，数据d的概率。

P(h)=类先验概率。这是假设h为真时的概率（与数据无关）

P(d)=预测器先验概率。这是数据的概率（与假设无关）

之所以称之为朴素是因为该算法假定所有的变量都是相互独立的（在现实生活大多数情况下都可以做这样的假设）。

如图，当天气是晴天的时候（第一列第一行），选手的状态是如何的呢？

在给定变量天气是晴天（sunny）的时候，为了判断选手的状态是‘yes’还是‘no’，计算概率，然后选择概率更高的作为输出。

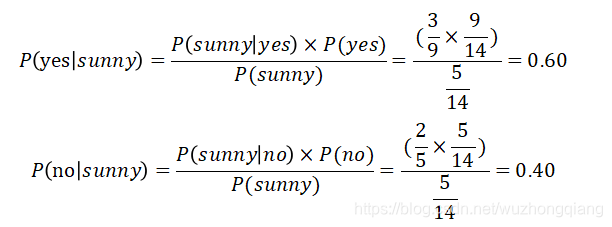
因此，当天气是晴天的时候，选手的状态是‘yes’

5. KNN（K近邻算法）
K最近邻算法是利用整个数据集作为训练集，而不是将数据集分成训练集和测试集。

当要预测一个新的输入实体的输出时，k最近邻算法寻遍整个数据集去发现k个和新的实体距离最近的实体，或者说，k个与新实体最相似的实体，然后得到这些输出的均值（对于回归问题）或者最多的类（对于分类问题）。而k的值一般由用户决定。

不同实体之间的相似度，不同的问题有不同的计算方法，包括但不限于：Euclidean distance 和Hamming distance。

无监督学习算法
6. 关联规则算法
关联规则算法在数据库的候选项集中用来挖掘出现频繁项集，并且发现他们之间的关联规则。关联规则算法在购物篮分析中得到了很好的应用。所谓的购物篮分析，是指找到数据库中出现频率最高的事物的组合。通常，如果存在关联规则：“购买了商品x的人，也会购买商品y”，我们将其记作：x–y。

比如，如果一个人购买了牛奶和糖，那么他很有可能会购买咖啡粉。在充分考虑了支持度（support）和置信度（confidence）后，得到关联规则。

支持度（support）检验项目集是否频繁。支持度的检验是符合Apriori原理的，即当一个项目集是频繁的，那么它所有的子集一定也是频繁的。

我们通过置信度（confidence）的高低，从频繁项集中找出强关联规则。

根据提升度（lift），从强关联规则中筛选出有效的强关联规则。

7. K-means算法
k-means算法是一个迭代算法的聚类算法，它将相似的数据化到一个簇（cluster）中。该算法计算出k个簇的中心点，并将数据点分配给距离中心点最近的簇。

k-means初始化：

a) 选择一个k值。如图6，k=3。

b) 随机分配每一个数据点到三个簇中的任意一个。

c) 计算每一个簇的中心点。如图6，红色，蓝色，绿色分别代表三个簇的中心点。

将每一个观察结果与当前簇比较：

a) 重新分配每一个点到距中心点最近的簇中。如图6，上方5个点被分配给蓝色中心点的簇。

重新计算中心点：

a) 为新分配好的簇计算中心点。如图六，中心点改变。

迭代，不再改变则停止：

a) 重复步骤2-3，直到所有点所属簇不再改变。

8. PCA主成分分析
主成分分析是通过减少变量的维度，去除数据中冗余的部分或实现可视化。基本的思路将数据中最大方差的部分反映在一个新的坐标系中，这个新的坐标系则被称为“主要成分”。其中每一个成分，都是原来成分的线性组合，并且每一成分之间相互正交。正交性保证了成分之间是相互独立的。

第一主成分反映了数据最大方差的方向。第二主成分反映了数据中剩余的变量的信息，并且这些变量是与第一主成分无关的。同样地，其他主成分反映了与之前成分无关的变量的信息。

集成学习技术
集成学习是一种将不同学习模型（比如分类器）的结果组合起来，通过投票或平均来进一步提高准确率。一般，对于分类问题用投票；对于回归问题用平均。这样的做法源于“众人拾材火焰高”的想法。

集成算法主要有三类：Bagging，Boosting 和Stacking。本文将不谈及stacking。

9. 使用随机森林Bagging
随机森林算法（多个模型）是袋装决策树（单个模型）的提升版。

Bagging的第一步是针对数据集，利用自助抽样法（Bootstrap Sampling method）建造多个模型。

所谓的自助抽样，是指得到一个由原始数据集中随机的子集组成的新的训练集。每一个这样的训练集都和原始训练集的大小相同，但其中有一些重复的数据，因此并不等于原始训练集。并且，我们将原始的数据集用作测试集。因此，如果原始数据集的大小为N，那么新的训练集的大小也为N（其中不重复的数据数量为2N/3），测试集的大小为N。

Bagging的第二步是在抽样的不同的训练集上，利用相同的算法建造多个模型。

在这里，我们以随机森林为例。决策树是靠每一个节点在最重要的特征处分离来减小误差的，但与之不同，随机森林中，我们选择了随机塞选的特征来构造分裂点。这样可以减小所得预测之间的相关性。

每一个分裂点搜索的特征的数量，是随机森林算法的参数。

因此，用随机森林算法实现的Bagging，每一个树都是用随机样本构造的，每一个分裂点都是用随机的预测器构造的。

10. 用Adaboost实现Boosting
a) 因为Bagging中的每一个模型是独立构造的，我们认为它是并行集成的。与之不同，Boosting中的每一个模型，都是基于对前一个模型的过失进行修正来构造的，因此Boosting是线性的。

b) Bagging中采用的是简单的投票，每一个分类器相当于一个投票（节点分裂，相当于进行一次投票），最后的输出是与大多数的投票有关；而在Boosting中，我们对每一个投票赋予权重，最后的输出也与大多数的投票有关——但是它却是线性的，因为赋予了更大的权重给被前一个模型错误分类的实体（拥有更大的权重，则其误差的影响被放大，有助于我们得到使得更小误差的模型）。

AdaBoost指的是自适应增强（Adaptive Boosting）

在上图，第一、二、三步中弱学习模型被称作决策树桩（一个一级的决策树只依据一个输入特征进行预测；一个决策树的根节点直接连接到它的叶子节点）。构造弱学习模型的过程持续到，a）达到用户定义的数量，或者 b）继续训练已经无法提升。第四步，将三个决策树桩组合起来。

第一步：从一个决策树桩开始，根据一个输入变量作出决定

从图中可以看见，其中有两个圆圈分类错误，因此我们可以给他们赋予更大的 权重，运用到下一个决策树桩中。

第二步：依据不同的输入变量，构造下一个决策树桩

可以发现第二个决策将会尝试将更大权重的数据预测正确。和如图的情况中， 我们需要对另外三个圆圈赋予更大的权重。

第三步：依据不同的输入变量，训练不同的决策树桩

之前步骤一样，只是这次被预测错误的是三角形的数据，因此我们需要对其赋 予更大的权重。

第四步：将决策树桩组合起来

我们将三个模型组合起来，显而易见，集成的模型比单个模型准确率更高。