@TOC

一.堆排序

1.使用向上还是向下调整建堆好？

(1)向上调整算法建堆的时间复杂度

void adjustup(HPDatatype* a, int child)//向上调整算法
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] < a[child])//以大堆为例
		{
			swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

1. 完整过程

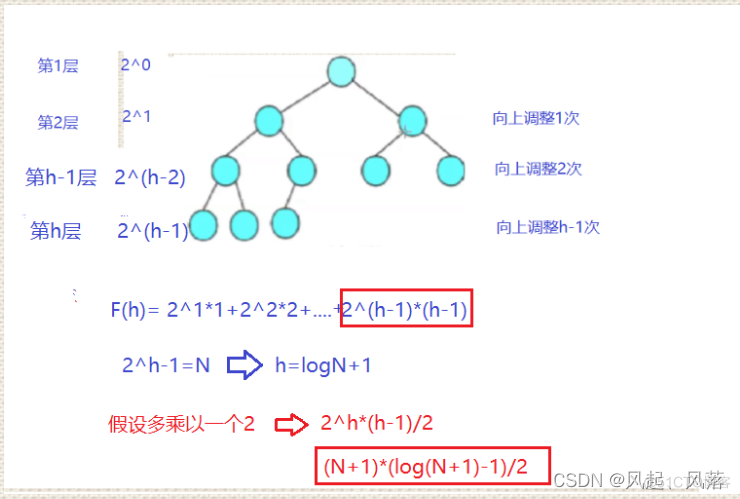
由于第一层不需要调整，所以从第二层开始 这里没有详细算，因为我们发现在最后的2^(h-1)*(h-1) 用公式拆分后，就可以算出结果
通过大O的渐进表示法， 时间复杂度为O(N * logN)

(2)向下调整算法建堆的时间复杂度

void adjustdown(HPDatatype* a, int parent,int size)//向下调整算法
{
	int child = parent * 2 + 1;//假设为左孩子
	while (child<size)
	{
		if (child+1<size&&a[child] < a[child + 1])//如果假设不成立，就为右孩子
		{
			child++;
		}
		if (a[parent] < a[child])//孩子大于父亲
		{
			swap(&a[parent], &a[child]);
			parent = child;
			child=parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

1.完整过程

• 由于2^h-1为二叉树总节点个数，所以最后一层为h-1, 但因向下调整算法是从倒数第二层的父节点开始的即 从h-2层开始，
• 这里不太懂为什么从倒数第二层的父亲节点开始 可以看：堆的带图详解

• 由于大O的渐进表示法，可以把时间复杂度看作为O(N)

(3)总结

• 因为 向上调整算法的时间复杂度为O(NlogN) ，而向下调整算法的时间复杂度为 O(N)
• 所以使用向下调整算法建堆更好

2. 排升序

(1) 建小堆

• 假设小堆如图所示

• 只能取到最小的节点，再次想要取次小的节点时会打乱节点之间的结构，从而需要重新建堆

• 而重新建堆的时间复杂度为O(N)，遍历一次数组的时间复杂度也为O(N)，没有效率

(2) 建大堆

• 假设为大堆所图所示
  

交换最大的节点与最后一个节点，此时左子树与右子树结构没有发生变化 当从最后一个节点到第二层完成交换时，
共操作了 2^h 次 ，N=2^h ，h=log N
即时间复杂度为O(logN)

3. 堆排序时间复杂度统计

在整体过程中，主要有 向下调整算法建堆 及 排序组成
向下调整算法建堆的时间复杂度为O(N)
排序的时间复杂度为O(logN)
即堆排序的时间复杂度为O(NlogN)

4.完整代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

void swap(int * s1, int * s2)
{
int tmp = 0;
tmp = *s1;
*s1 = *s2;
*s2 = tmp;
}
void adjustdown(int * a, int parent, int size)//向下调整算法
{
int child = parent * 2 + 1;//假设为左孩子
while (child < size)
{
if (child + 1 < size && a[child] < a[child + 1])//如果假设不成立，就为右孩子
{
child++;
}
if (a[parent] < a[child])//孩子大于父亲
{
swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void print(int* a, int n)
{
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
}
void heapsort(int* a, int n)//堆排序——升序
{
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)//使用向下调整算法 时间复杂度为O(N)
{
adjustdown(a, i, n);
}

int end = n - 1;//排升序，建大堆 时间复杂度为O(logN)
while (end > 0)//end作为下标当为0时，说明只剩下一个数，不需要调整
{
swap(&a[0], &a[end]);//交换最大的数与最后一个数的位置，并将前n-1个数再次向下调整
adjustdown(a, 0, end);//此时end作为整体调整的个数
end--;
}
}
int main()
{
int arr[] = { 27,15,19,18,28,34,65,49,25,37 };
int n = sizeof(arr) / sizeof(arr[0]);
heapsort(arr, n);
print(arr, n);

return 0;
}

二 、 TOPK问题

1. 概念

即求数据结合中前k个最大的元素或者最小的元素，一般情况下数据量比较大

2.两种方法

第一种

建立一个N个数的大堆，删除k次，依次取堆顶
这种方法我们在上一篇实现过，若想看点击：堆的带图详解

缺陷

假设N很大，k很小，比如N=100亿 k=10
1G=1024 * 1024 * 1024Byte 约等于 10亿Byte
100 亿个整数 则需要 40G空间，
正常来说我们把数据放入内存中，再用堆去实现，但若数据太大，内存存不下,直接在磁盘文件中，就不会能在建堆了
40G属于数据太大的情况，所以不能进入内存中

第二种

思想

建立k个数小堆，依次遍历数据，比堆顶的数据大，就进行交换，再向下调整，最后最大的k个数就在小堆中

过程

假设共有如上的数据，n =6 ，k=3

• 取前k个数据建立一个小堆

再取剩余的数据依次与其比较，若比堆顶数据大，则赋值，同时进行向下调整，使堆顶为最小的数

3.完整代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
void swap(int* s1, int* s2)
{
int tmp = 0;
tmp = *s1;
*s1 = *s2;
*s2 = tmp;
}
void adjustdown(int* a, int parent, int size)//向下调整算法 这里以小堆为例
{
int child = parent * 2 + 1;//假设为左孩子
while (child < size)
{
if (child + 1 < size && a[child] > a[child + 1])//如果假设不成立，就为右孩子
{
child++;
}
if (a[parent] > a[child])//孩子小于父亲  
{
swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
int main()
{
int n = 0;
int k = 0;
printf("请输入数字:>");
scanf("%d%d", &n, &k);
FILE* pf = fopen("qwe.txt", "w");
if (pf == NULL)
{
perror("fopen tail");
exit(-1);
}
int i = 0;
srand(time(0));
for (i = 0; i < n; i++)//将n个数据传入文件中
{
int ret = rand();
fprintf(pf, "%d\n", ret);
}
fclose(pf);//输入文件数据后就关闭
//////////////////////////////////////////
FILE* cout = fopen("qwe.txt", "r");
if (cout == NULL)
{
perror("fopen tail");
exit(-1);
}
int* minheap = (int*)malloc(sizeof(int) * k);
if (minheap == NULL)
{
perror(" malloc fail");
}

for (i = 0; i < k; i++)//将k个数据传入数组中 即使用k个数建堆
{
fscanf(cout, "%d", &minheap[i]);
}

for (i = (k - 1 - 1) / 2; i >= 0; i--)//使用向下调算法建小堆
{
adjustdown(minheap, i, k);
}

int val = 0;
while (fscanf(cout, "%d", &val)!=EOF)//将文件剩余的数据继续传入数组中比较
{
if (val > minheap[0])//如果val值比堆顶数据大
{
minheap[0] = val;
adjustdown(minheap, 0, k);//向下调整再次找到最小的堆顶
}
}



for (i = 0; i < k; i++)
{
printf("%d ", minheap[i]);
}
fclose(cout);
cout = NULL;
return 0;
}