2025-11-19：选择不同 X 值三元组使 Y 值之和最大。用go语言，给定两个长度相同的整数数组 x 和 y（长度为 n）。

从下标集合 {0,1,…,n-1} 中选出三个不同的位置 i、j、k，且这三处在 x 数组上的值两两不相同（即 x[i]、x[j]、x[k] 三者互异）。

要求使对应的 y 值之和 y[i] + y[j] + y[k] 尽可能大。

若不存在满足 x 值互异且下标互异的三元组，则返回 -1。

n == x.length == y.length。

3 <= n <= 100000。

1 <= x[i], y[i] <= 1000000。

输入：x = [1,2,1,3,2], y = [5,3,4,6,2]。

输出：14。

解释：

选择 i = 0（x[i] = 1，y[i] = 5），j = 1（x[j] = 2，y[j] = 3），k = 3（x[k] = 3，y[k] = 6）。

选出的三个 x 中的值互不相同。5 + 3 + 6 = 14 是我们能获得的最大值。因此输出为 14。

题目来自力扣3572。

分步骤详细过程

1. 构建映射（字典）以记录每个x值对应的最大y值
   首先，代码初始化一个空的映射（map结构），其键（key）为x数组中的值，值（value）为该x值在所有出现位置中所对应的最大y值。接着，程序同时遍历x和y数组。对于每个下标i，它检查x[i]是否已经存在于映射中。如果不存在，则将x[i]作为新键加入映射，并将y[i]作为其对应的值。如果x[i]已存在，则比较当前存储的y值与新的y[i]，并将映射中的值更新为两者中的较大者。这个过程确保了在遍历结束后，对于每一个不同的x值，映射中都只保存了其对应的最大y值。

2. 检查唯一x值的数量是否满足条件
   在构建完映射后，代码检查映射中不同键（即不同x值）的数量。如果这个数量小于3，则说明在所有的下标中，无法找到三个x值互不相同的元素，因此直接返回-1，表示不存在满足条件的三元组。

3. 提取并排序最大的y值
   如果唯一x值的数量大于等于3，则从映射中提取所有的值（即每个唯一x值对应的最大y值），形成一个列表。然后，将这个列表中的元素按照从大到小（降序）进行排序。这样，列表最前面的元素就是全局最大的y值。

4. 计算最大和
   最后，代码从降序排序后的列表中取出前三个元素（也就是最大的三个y值），将它们的数值相加，得到的和即为所求的最大可能总和。这个结果被返回作为答案。

复杂度分析

• 总的时间复杂度：该过程的时间复杂度主要由两个操作决定：遍历数组构建映射和排序唯一y值列表。遍历数组的时间复杂度为O(n)，其中n是数组的长度。排序操作的时间复杂度为O(u log u)，其中u是唯一x值的数量（即映射的大小）。在最坏情况下，u等于n，因此排序复杂度可达O(n log n)。综上，总的时间复杂度为O(n log n)。
• 总的额外空间复杂度：算法需要额外的空间来存储映射和唯一y值的列表。映射最多存储u个键值对，列表存储u个元素。因此，额外空间复杂度为O(u)。在最坏情况下（u = n），额外的空间复杂度为O(n)。

这个方法通过映射高效地聚合了每个x值对应的最大y值，并通过排序快速定位最大的三个值，从而在保证正确性的同时实现了较高的效率。

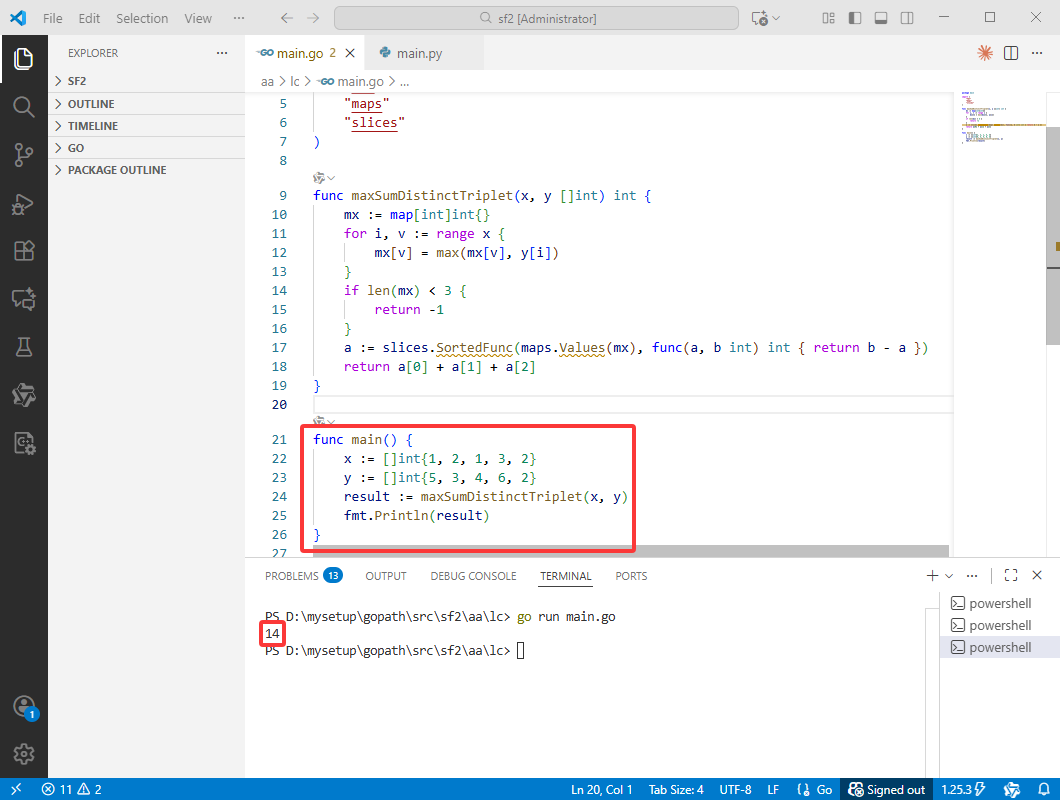
Go完整代码如下：

package main

import (
	"fmt"
	"maps"
	"slices"
)

func maxSumDistinctTriplet(x, y []int) int {
	mx := map[int]int{}
	for i, v := range x {
		mx[v] = max(mx[v], y[i])
	}
	if len(mx) < 3 {
		return -1
	}
	a := slices.SortedFunc(maps.Values(mx), func(a, b int) int { return b - a })
	return a[0] + a[1] + a[2]
}

func main() {
	x := []int{1, 2, 1, 3, 2}
	y := []int{5, 3, 4, 6, 2}
	result := maxSumDistinctTriplet(x, y)
	fmt.Println(result)
}

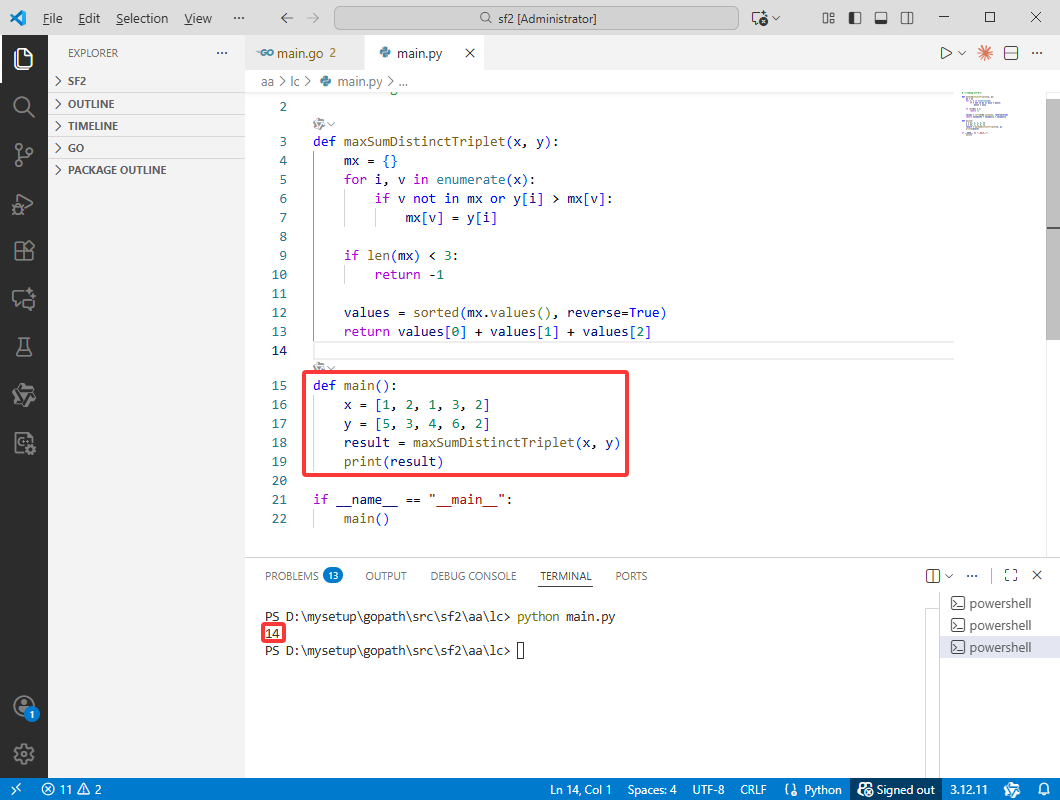
Python完整代码如下：

# -*-coding:utf-8-*-

def maxSumDistinctTriplet(x, y):
    mx = {}
    for i, v in enumerate(x):
        if v not in mx or y[i] > mx[v]:
            mx[v] = y[i]
    
    if len(mx) < 3:
        return -1
    
    values = sorted(mx.values(), reverse=True)
    return values[0] + values[1] + values[2]

def main():
    x = [1, 2, 1, 3, 2]
    y = [5, 3, 4, 6, 2]
    result = maxSumDistinctTriplet(x, y)
    print(result)

if __name__ == "__main__":
    main()

C++完整代码如下：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <algorithm>

using namespace std;

int maxSumDistinctTriplet(const vector<int>& x, const vector<int>& y) {
    unordered_map<int, int> mp;

    // 构建 map: 对每个 x[i] 只保留对应最大的 y[i]
    for (size_t i = 0; i < x.size(); i++) {
        int key = x[i];
        int val = y[i];
        if (mp.count(key)) {
            mp[key] = max(mp[key], val);
        } else {
            mp[key] = val;
        }
    }

    if (mp.size() < 3) return -1;

    // 提取所有 value
    vector<int> vals;
    vals.reserve(mp.size());
    for (auto& p : mp) {
        vals.push_back(p.second);
    }

    // 降序排序
    sort(vals.begin(), vals.end(), greater<int>());

    // 返回最大三个值的和
    return vals[0] + vals[1] + vals[2];
}

int main() {
    vector<int> x = {1, 2, 1, 3, 2};
    vector<int> y = {5, 3, 4, 6, 2};

    int result = maxSumDistinctTriplet(x, y);
    cout << result << endl;

    return 0;
}