算数混合四则运算求值
@TOC
- [问题]
利用算符优先关系,实现对算术四则混合运算表达式的求值
- [要求]
输入的形式:表达式,例如2*(3+4)
包含的运算符只能有’+’ 、’-’ 、’*’ 、’/’ 、’(’、 ‘)’;
输出的形式:运算结果,例如2*(3+4)=14;
程序所能达到的功能:对表达式求值并输出
- 思路:利用栈实现表达式求值,需要思考如下问题:
算符的优先级
字符转换成数字(包括解析小数)
- 主要思路:
算术表达式有三种类型:前缀,中缀,后缀表达式,而这里主要利用的是中缀和后缀表达式
- 示图:
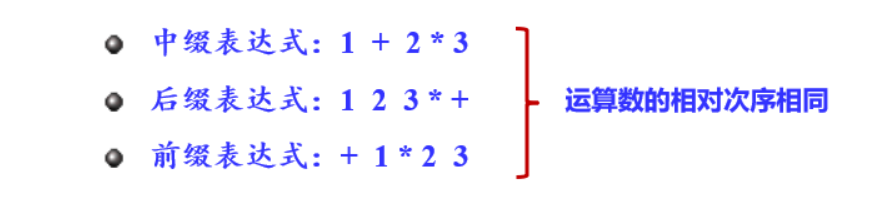
- 中缀表达式:运算符位于操作数中间
中缀表达式的运算规则:“先乘除,后加减,从左到右计算,先括号内,后括号外”
即中缀表达式不仅要依赖运算符优先级,而且还要处理括号
- 后缀表达式:运算符在操作数的后面
已考虑了运算符的优先级,而且越放在前面的运算符来越优先执行
没有括号,只有操作数和运算符
我们平常使用的是中缀表达式,而后缀表达式运算的优先已经好了,所以我们用后缀表达式进行四则计算
-
步骤一:中缀表达式转后缀表达式
-
示图:
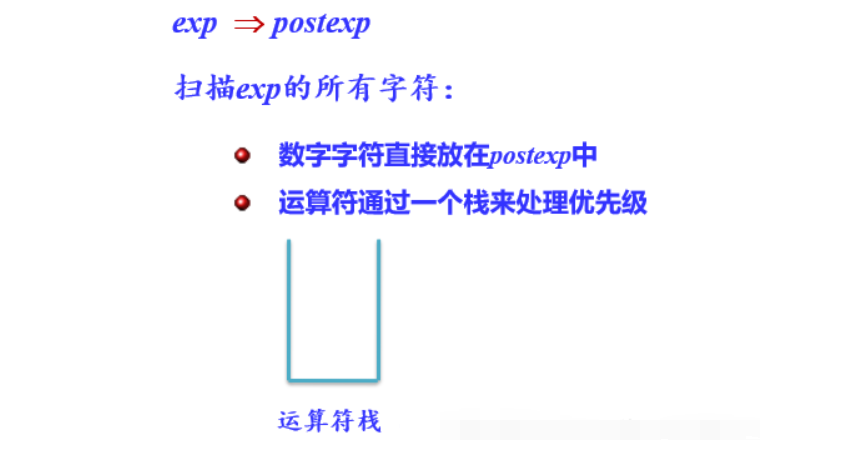
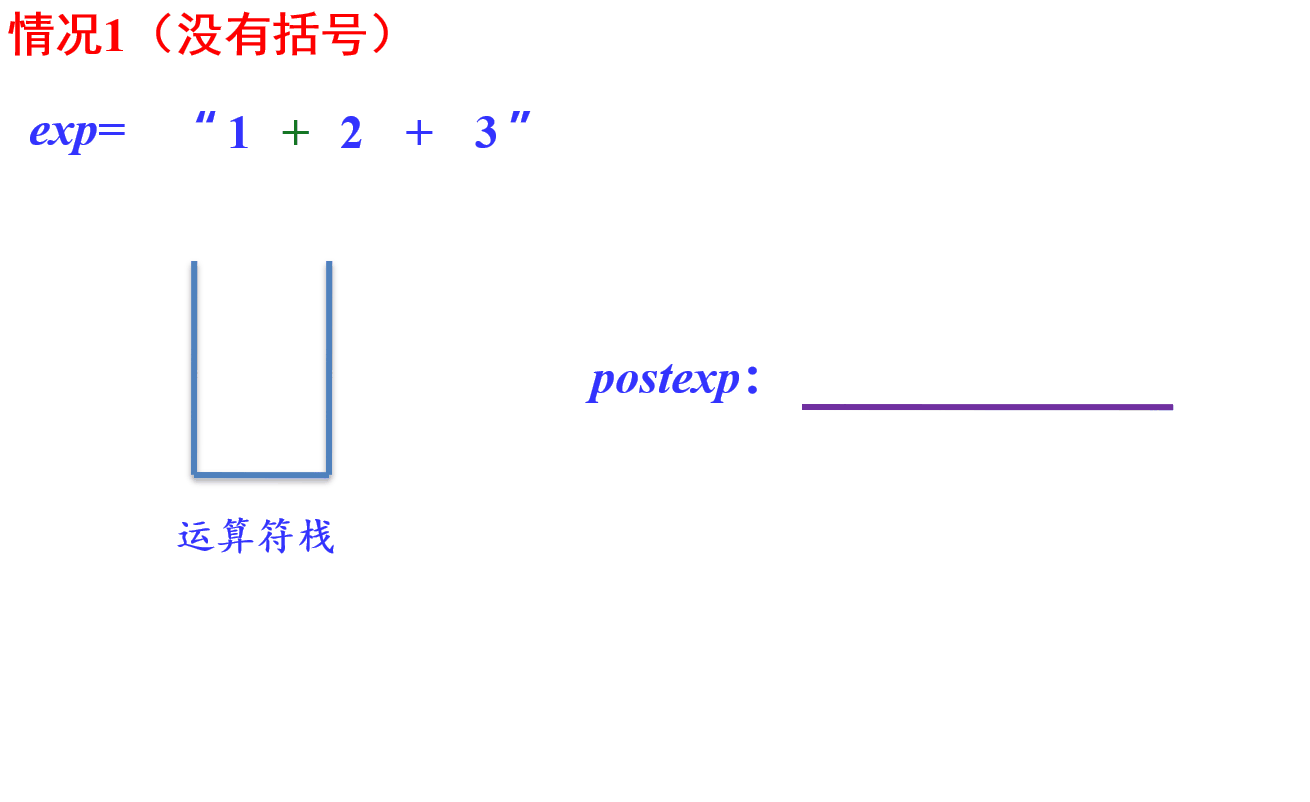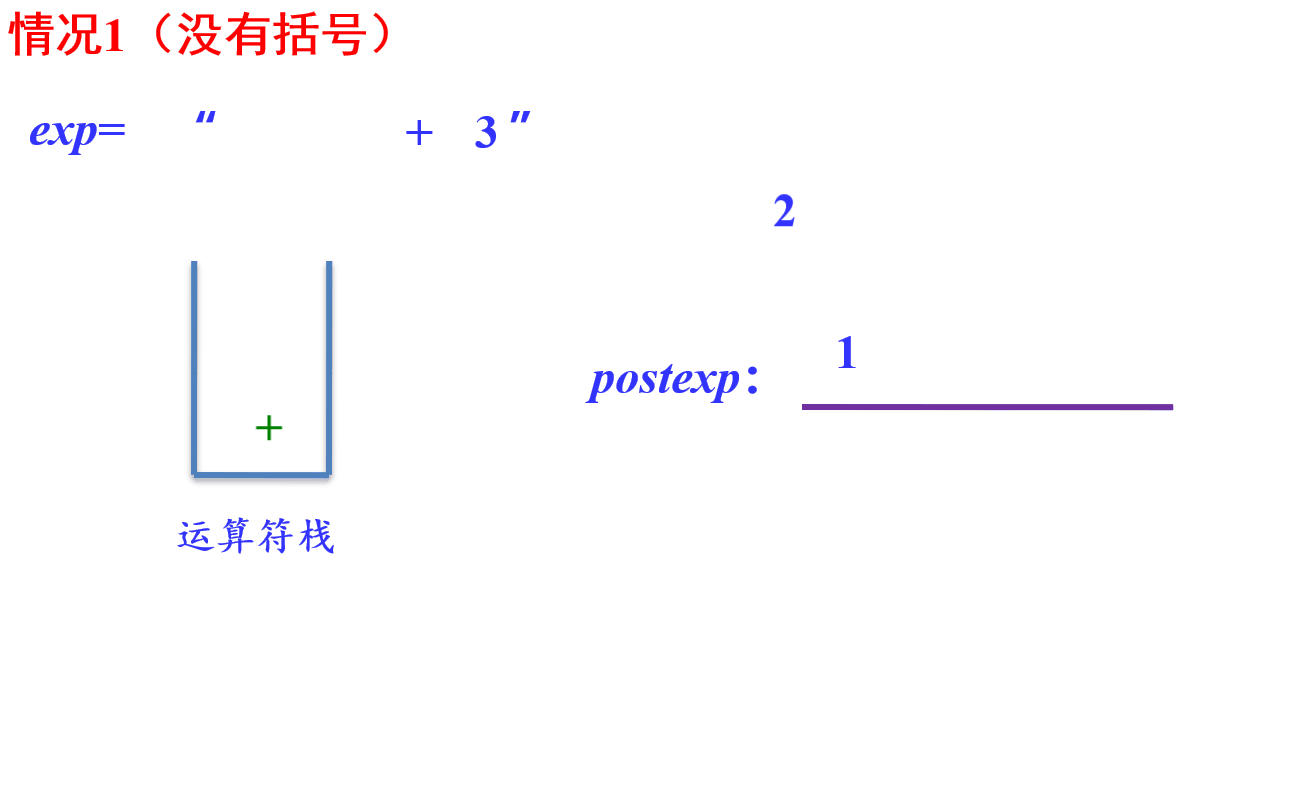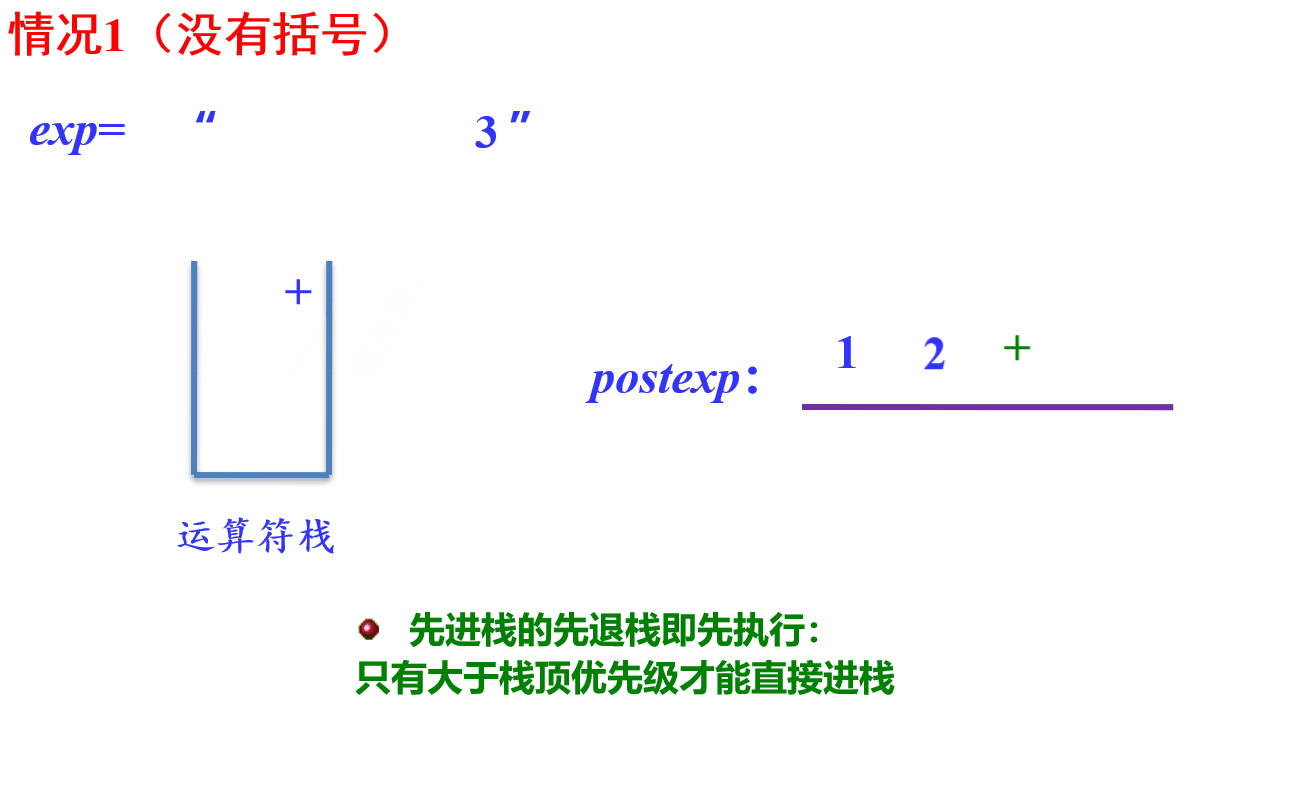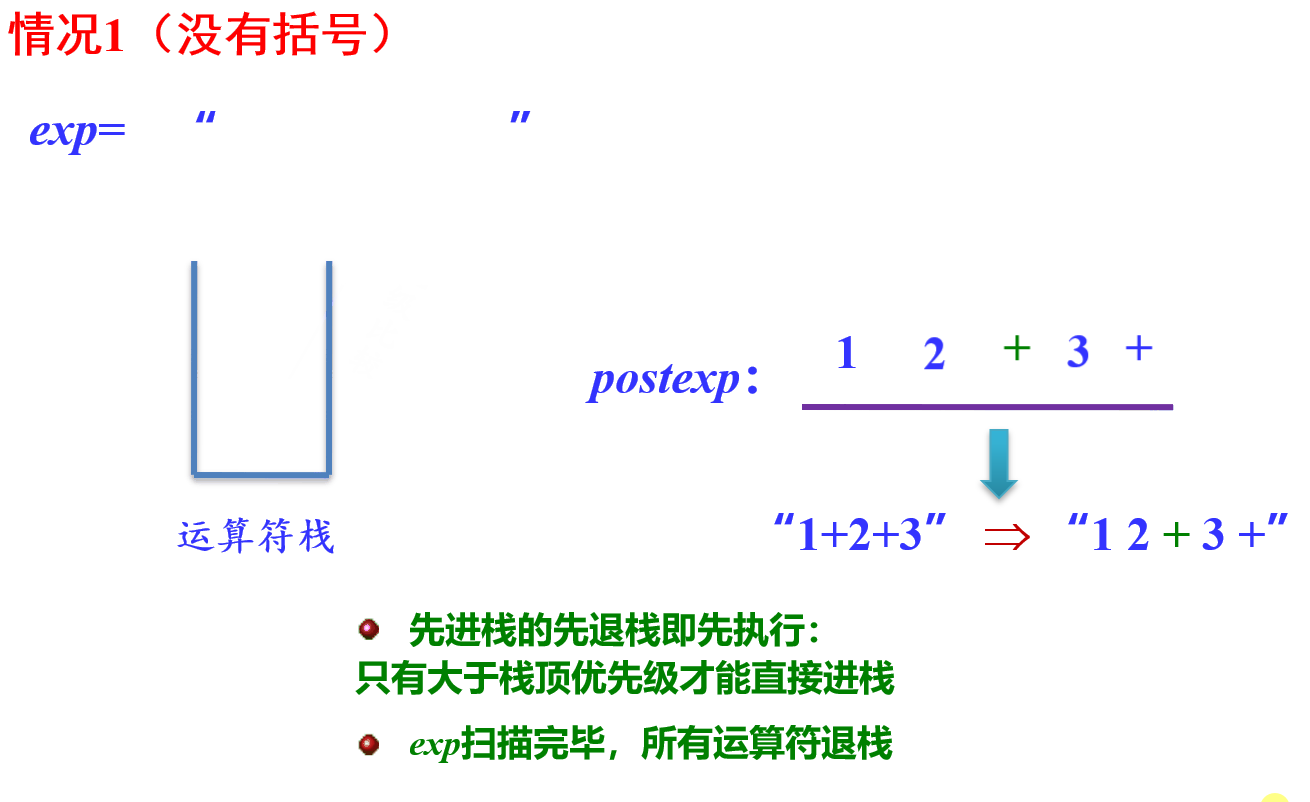
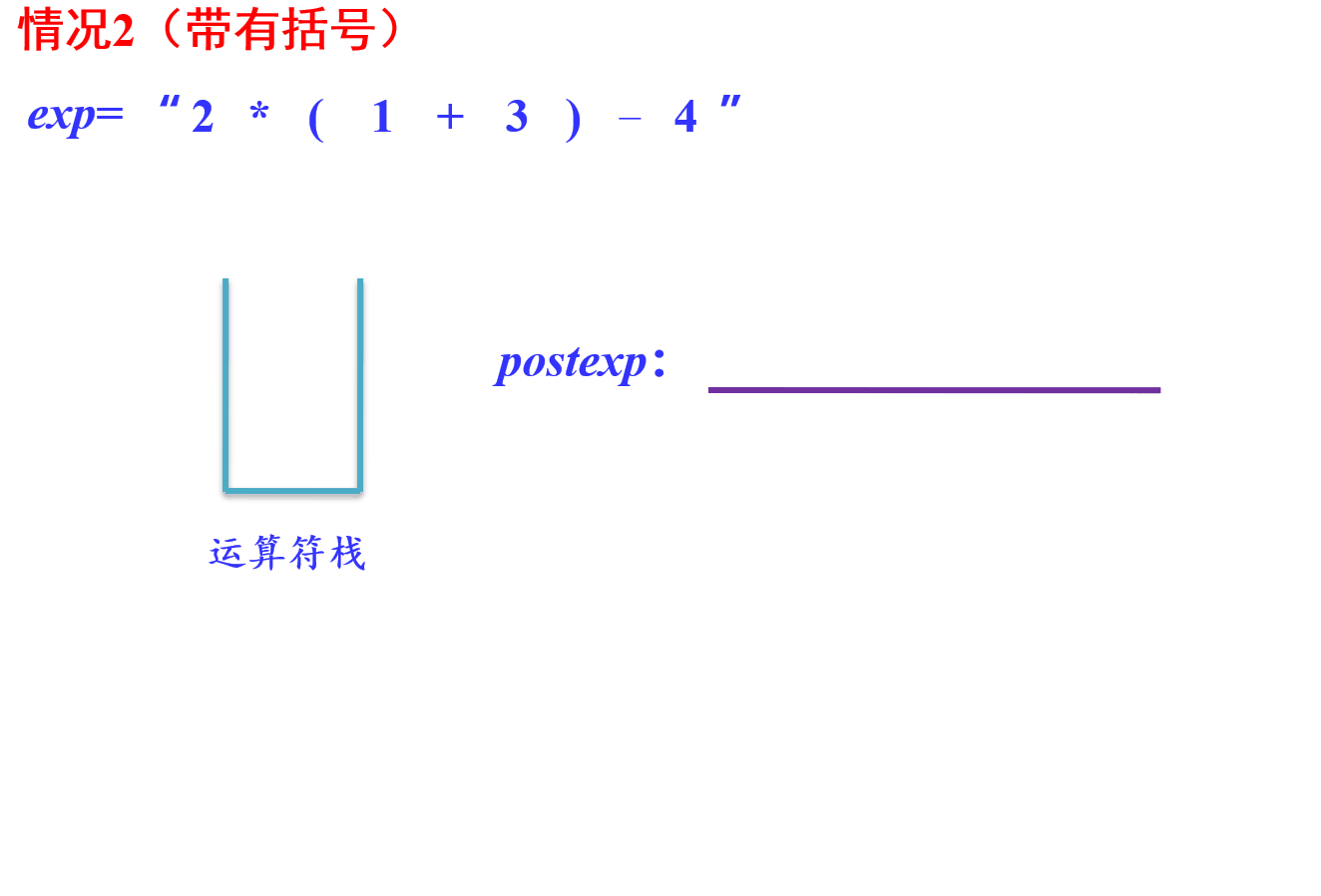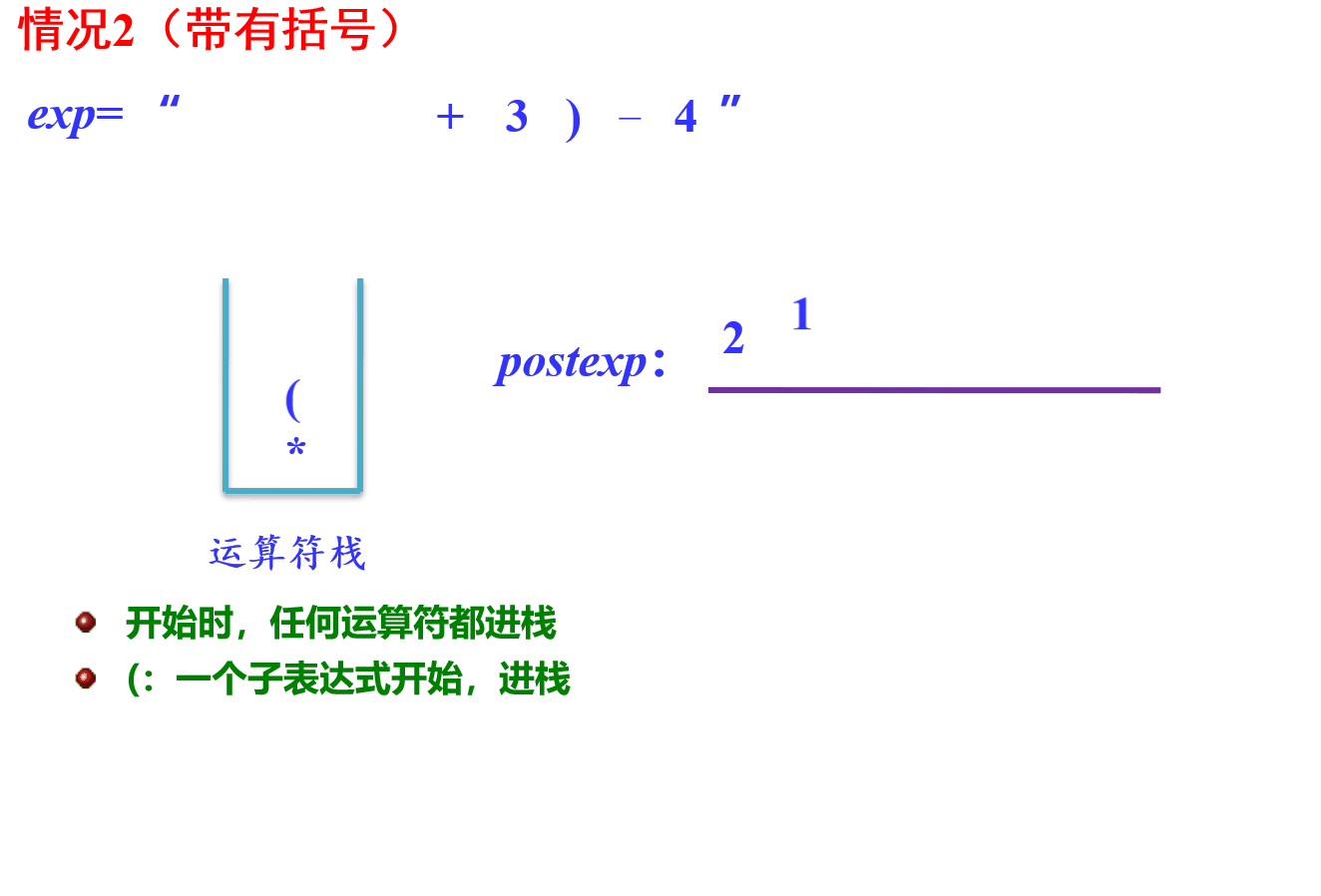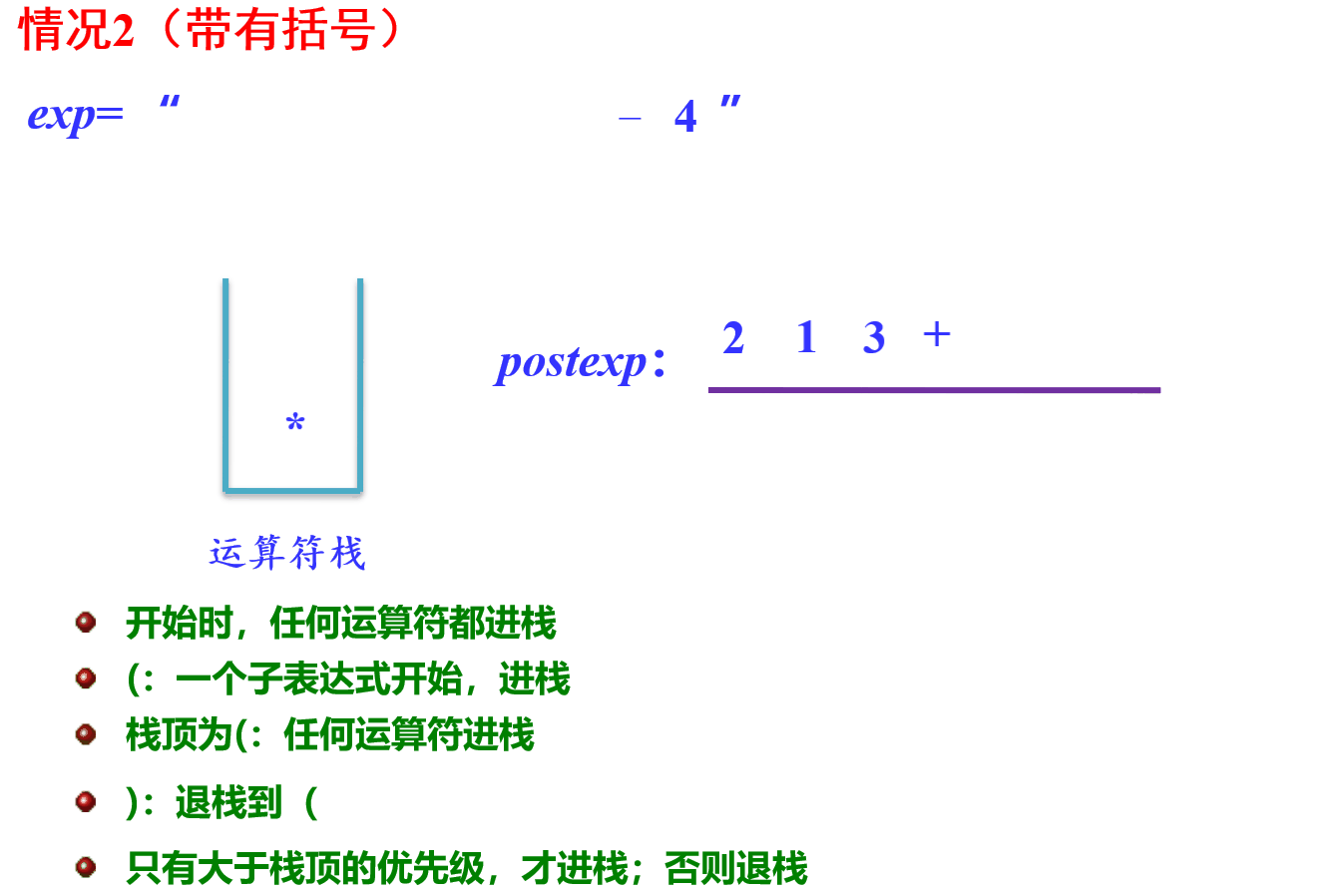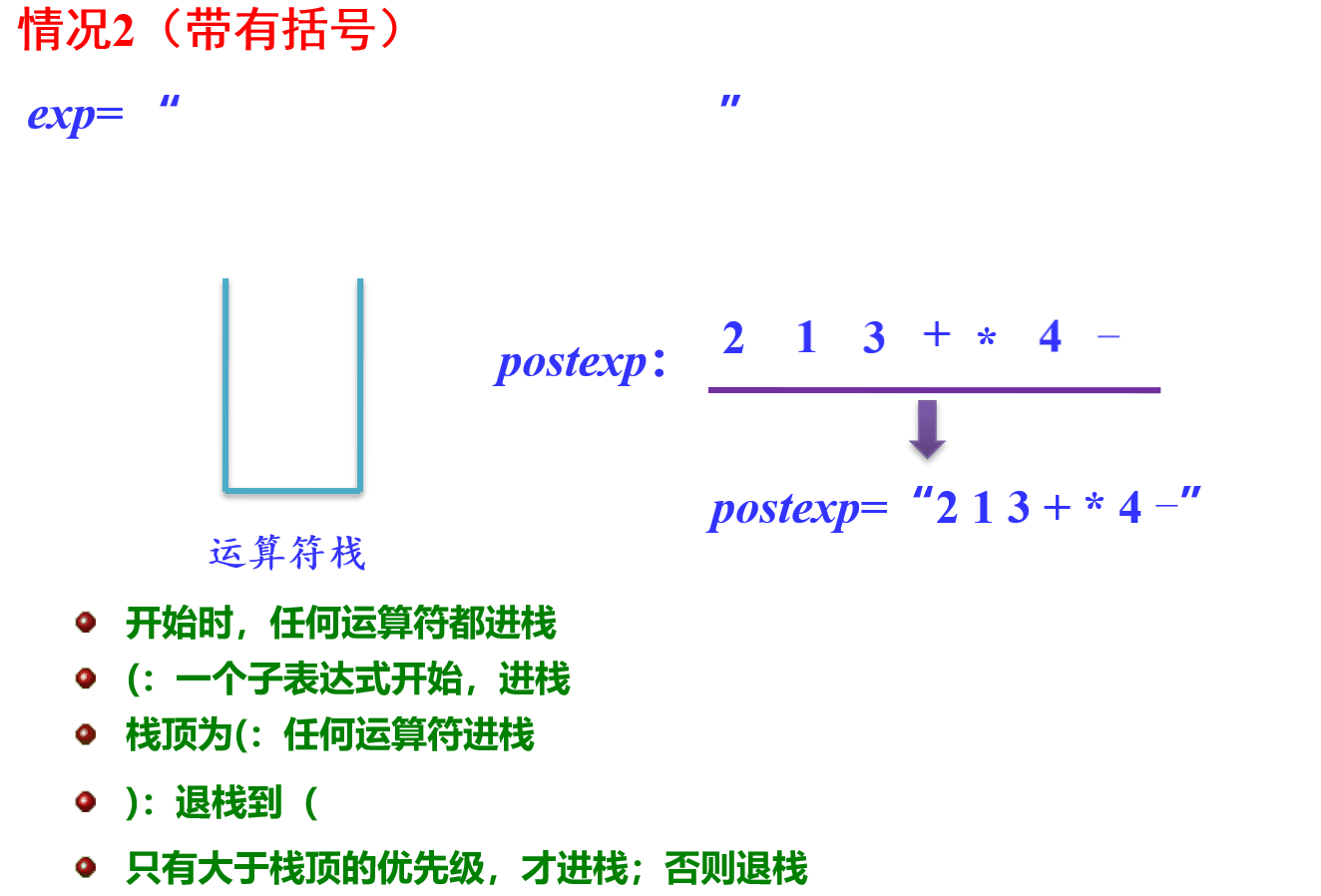
- 过程实现:
遍历中缀表达式
遇到数字直接放入后缀表达式
遇到左括号入栈
遇到右括号则将栈里的运算符一直出栈到左括号出栈,并按出栈顺序放入后缀表达式中(达到一个去括号的效果)
遇到 * / 运算符,因为是较高优先级运算符,所以直接入栈
遇到 + - 运算符,因为是较低优先级运算符,所以需要先将栈顶高于或等于其优先级的运算符 * / 给出栈并放入后缀表达式中(遇到左括号需要停止)
遇到其他字符则直接报错退出程序
当遍历完后再将栈中剩余的运算符给出栈并放入后缀表达式中
- 步骤二:依靠后缀表达式计算结果
因为后缀表达式已经达到去括号,决定运算符优先级的效果了,所以可以直接计算
- 示图:

- 过程实现:
遍历后缀表达式
遇到数字直接入栈
遇到运算符则将栈顶出栈,取出两个操作数(注:左操作数是第二个出栈的数值)
根据操作符将两操作数进行运算得到得结果给入栈到栈中
遍历结束后,栈顶的数据就是最后的结果
- 思考:
优先级:后缀表达式已经将运算符的优先级给处理好了
字符转浮点:从中缀表达式转后缀时,遍历到数字或小数点则一直进行放入到后缀表达式中,并在最后放一个空格做分隔符,处理后缀表达式时遇到数字就依靠分隔符确定区间并转成浮点数
- 实现代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<string>
#include<stack>
#include <stdlib.h>
using namespace std;
string TransExpToPostexp(string& exp)
{
stack<char> optr;
string postexp;
for (int i = 0; i < exp.size(); i++)
{
if ((exp[i] >= '0' && exp[i] <= '9') || exp[i] == '.')//是数字直接进字符串
{
postexp += exp[i];
while ((exp[i+1] >= '0' && exp[i+1] <= '9') || exp[i+1] == '.')
postexp += exp[++i];
postexp += ' ';//分隔
}
else
{
if (exp[i] == '(')//是左括号进栈
optr.push(exp[i]);
else if (exp[i] == ')')//遇到右括号则出栈到左括号出栈
{
while (!optr.empty())
{
if (optr.top() == '(')//遇到左括号则出栈并退出
{
optr.pop();
break;
}
else//遇到其他操作符则添加到后缀表达式中并出栈
{
postexp += optr.top();
postexp += ' ';//分隔
optr.pop();
}
}
}
else if (exp[i] == '*' || exp[i] == '/')
{
optr.push(exp[i]);
}
else if (exp[i] == '-' || exp[i] == '+')
{
while (!optr.empty()&&optr.top()!='(')//小于等于栈顶操作符数据,则出栈*
{
postexp += optr.top();
postexp += ' ';//分隔
optr.pop();
}
//进栈
optr.push(exp[i]);
}
else//表达式错误
{
perror("exp error!");
exit(1);
}
}
}
//遍历结束,剩余操作符出栈
while (!optr.empty())
{
postexp += optr.top();
postexp += ' ';//分隔
optr.pop();
}
return postexp;
}
double Calculate(string postexp)
{
stack<double> data;//数据栈
for (int i = 0; i < postexp.size(); i++)
{
if (postexp[i] >= '0' && postexp[i] <= '9')//是数字则入栈
{
int left = i, right = i;
while (postexp[right] != ' ')
right++;
double num = atof(postexp.substr(left,right).c_str());//字符串转浮点
//cout << num << endl;
data.push(num);
i = right;
}
else//遇到操作符
{
//取栈顶两数据,注意先后顺序,后一个才是左操作数
double right = data.top();
data.pop();
double left = data.top();
data.pop();
//判断操作符,得到数据再入栈
char optr = postexp[i];
switch (optr)
{
case '+':
data.push(left + right);
break;
case '-':
data.push(left - right);
break;
case '*':
data.push(left * right);
break;
case '/':
data.push(left / right);
break;
default:
perror("optr error");
break;
}
cout << data.top() << endl;
i++;
}
}
return data.top();
}
int main()
{
string str;
while (cin >> str)
{
string postexp=TransExpToPostexp(str) ;
cout << postexp << endl;
cout << Calculate(postexp) << endl;
}
return 0;
}
- 测试:
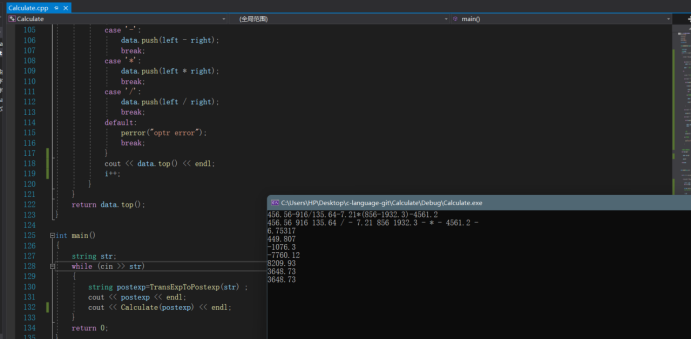
- 点赞
- 收藏
- 关注作者


评论(0)