内容概况

一、GraphSAGE模型

从内容推荐到蛋白质功能识别，大型图中节点的低维嵌入在各种预测任务中被证明是非常有用的。然而，现有的大多数方法都要求在训练嵌入时，需要图中的所有节点都存在。以往的方法都是 $transductive$ 式的，而后来提出的 $inductive$（直推式） 式的 $GraphSAGE$ 算法利用节点特征信息(如文本属性)有效地为未知的数据生成节点嵌入，GraphSAGE并非训练每个节点的单独嵌入，而是学习一个函数，该函数通过从节点的局部邻域采样和聚合特征来生成嵌入。该算法在三个 $inductive$（归纳式） 式节点分类 $benchmarks$ 上超过 $baselines$ ：能够根据引文和 $Reddit$ 数据对演化信息图中未知的节点进行分类，实验表明使用一个 $PPI$（$protein-protein$ $interactions$）多图数据集，算法可以泛化到完全未见过的图上。

在大规模图中，节点的低维向量embedding被证明了作为各种预测和图分析任务的特征输入是极为有用的。顶点embedding的基本思想是使用降维将节点图邻域的高维信息提取成密集的向量嵌入。这些节点嵌入可以提供给下游机器学习系统，并帮助完成节点分类、聚类和链接预测等任务。

以往的工作一般是从单一的固定图中抽取顶点嵌入，现实中的应用需要能够快速地从不可见的节点或者全新的（子）图中生成 $embedding$，这种生成式能力对高吞吐量的机器学习系统很重要，特别是当数据处于一个不断演化的图中，不断加入新节点的情况下（如Reddit上的帖子、Youtube上的用户和视频）。

生成节点嵌入的归纳算法也有助于在具有相同特征形式的图之间进行泛化：比如我们可以在模型生物的蛋白质相互作用图上训练一个embedding生成器，然后利用这个生成器方便地为收集的新生物数据生成节点嵌入。

归纳式顶点嵌入问题比直推式难很多，因为要推广到未知节点需要将新观察的子图与算法已经优化过的节点嵌入“对齐”（aligning）。归纳式学习框架必须学会识别一个节点邻域的结构属性，它揭示了图中节点的局部角色和全局位置。

大部分现有的生成顶点嵌入的方法都是直推式的。这些方法中的大多数使用基于矩阵分解的目标直接优化每个节点的嵌入，而不会自然地推广到看不见的数据，因为它们是对单个固定图中的节点进行预测。这些方法可以修改为归纳式的（比如DeepWalk就可以），但是这些修改在计算上很昂贵，在做出新的预测之前需要额外的梯度下降。GraphSAGE属于归纳式。

二、YelpChi评论图数据集上的异常检测

2.1题目：反欺诈检测

通过图上的洗钱账户识别的例子来介绍和实现一个简单的反洗钱识别算法，洗钱账户识别是给出一张金融行为图（如节点为账户，交易为边）需要判断图中哪些节点是有洗钱行为的异常节点。这里直接用YelpChi图数据集模拟反洗钱欺诈的数据集了，主要看后面模型的原理。

代码模块：

• 加载和预处理数据、
• 构造和提取特征、
• 构建图：根据边列表生成邻接矩阵
• 训练分类器：这里使用能够图的拓扑结构，和缓解类别不平衡状况的自动加权图卷积神经网络
• 训练得到一个可以应用的反洗钱识别工具。

反洗钱识别是依据金融行为图的特征对图中的节点进行分类，识别图中的有洗钱行为的异常节点，可以形式化为一个类别不平衡的二分类问题，其中无洗钱行为的正常节点为多数类（负类），有洗钱行为的异常节点为少数类（正类）。

2.2 数据集介绍

YelpChi数据集：基于Yelp数据集上的一个行为图数据集，数据集中的数据以稀疏矩阵的形式存在。该数据集经常用于节点分类、欺诈检测、异常检测等的研究任务上。

Yelp垃圾评论数据集包括Yelp过滤(垃圾)和推荐(合法)的酒店和餐厅评论。Yelp-Fraud数据集上执行一个垃圾邮件审查检测任务，该任务是一个二元分类任务。YelpChi从SpEagle上提取了32个手工特性作为Yelp-Fraud的原始节点特性，基于前人研究发现意见欺假者在用户、产品、评论文本、时间等方面存在联系，将评论作为图中的节点，设计了三种关系:

1. R-U-R:连接同一用户发布的评论;
2. R-S-R:连接同一产品同一星级(1-5星)下的评论;
3. R-T-R:连接同一个月发布的同一产品下的两个评论。

数据集下载：https://github.com/YingtongDou/CARE-GNN/tree/master/data

三、代码实现

!unzip -o 'datasets/data/YelpChi.zip' -d 'work/' 
unzip:  cannot find or open datasets/data/YelpChi.zip, datasets/data/YelpChi.zip.zip or datasets/data/YelpChi.zip.ZIP.
#统一导入工具包
import time
import os
import random
import pickle
import numpy as np
import scipy.sparse as sp
import copy as cp
import torch
import torch.nn as nn
from torch.nn import init
from scipy.io import loadmat
from sklearn.metrics import f1_score, accuracy_score, recall_score, roc_auc_score, average_precision_score
from sklearn.model_selection import train_test_split
from collections import defaultdict
#全局初始化配置参数，固定随机种子
DEBUG = False # Debug模式可快速跑通代码，非Debug模式可得到更好的结果
VERBOSE = True # Verbose模式打印更多参数
seed=99
batch_size=1024
lr=0.1
lambda_1=2
lambda_2=1e-3
emb_size=64
num_epochs=2 if DEBUG else 31
test_epochs=10
under_sample=1
step_size=2e-2
no_cuda=1

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
 

1.图数据准备

使用金融行为数据集，首先读入数据，再对数据做简单的分析，整体步骤如下：

（1）数据预处理说明

（2）数据加载说明

（3）训练集、验证集、测试集划分

1.1 数据预处理说明

使用scipy.io中的loadmat()函数读取MATLAB格式的文件（后缀为.mat），函数接受文件路径作为参数，根据边的类型，读出以稀疏矩阵形式存储的数据，转换为邻接列表并存储。

# 对数据进行预处理,由稀疏矩阵得到邻接列表
def sparse_to_adjlist(sp_matrix, filename):
    # 加入自循环
    homo_adj = sp_matrix + sp.eye(sp_matrix.shape[0])
    # 初始化邻接列表
    adj_lists = defaultdict(set)
    edges = homo_adj.nonzero()
    edge_cnt = 0
    # 根据邻接矩阵计算邻接列表
    for index, node in enumerate(edges[0]):
        adj_lists[node].add(edges[1][index])
        adj_lists[edges[1][index]].add(node)
        edge_cnt += 1
    # 存储邻接列表
    with open(filename, 'wb') as file:
        pickle.dump(adj_lists, file)
    file.close()
    return edge_cnt

# 读入mat格式的数据进行预处理
prefix = 'work/'
yelp = loadmat(prefix + 'YelpChi.mat')
# 输入数据中的邻接矩阵
yelp_homo = yelp['net_rur']
# 计算邻接列表
cnt_homo = sparse_to_adjlist(yelp_homo, prefix + 'yelp_homo_adjlists.pickle')
# 输出数据图的节点数和边数
print('Node',yelp_homo.shape[0], 'Edge', cnt_homo)

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
 

Node 45954 Edge 144584
可以看到行为图数据中节点和边的数量。

1.2 数据加载说明

读取节点特征和节点标签，读取上一步处理过的根据边的类型生成的图数据

prefix = 'work/'
# 读入mat格式的数据
data_file = loadmat(prefix + 'YelpChi.mat')
labels = data_file['label'].flatten()
feat_data = data_file['features'].todense().A
# 加载预处理后的邻接列表
with open(prefix + 'yelp_homo_adjlists.pickle', 'rb') as file:
    homo = pickle.load(file)
file.close()
# 计算数据的类别不平衡程度
print('Class imbalance racio:{:.4f}'.format(np.mean(labels)))

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

Class imbalance racio 0.14529747138442792
行为数据集中异常节点类别为1，正常节点类别为0，可以看到异常节点只占总节点数的14.53%，有一定的类别不平衡现象。

接下来将数据集分割为训练集、验证集、测试集，并分割训练集中的正常节点和异常节点

# 将数据集按照类别的正负分开
def pos_neg_split(nodes, labels):
    pos_nodes = []
    neg_nodes = cp.deepcopy(nodes)
    aux_nodes = cp.deepcopy(nodes)
    for idx, label in enumerate(labels):
        if label == 1:
            pos_nodes.append(aux_nodes[idx])
            neg_nodes.remove(aux_nodes[idx])

    return pos_nodes, neg_nodes
# 设置随机数种子
np.random.seed(seed)
random.seed(seed)
index = list(range(len(labels)))
# 划分训练集和测试集
idx_train, idx_test, y_train, y_test = train_test_split(index, labels, stratify=labels, test_size=0.60, random_state=2, shuffle=True)
train_pos, train_neg = pos_neg_split(idx_train, y_train)

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
 

if VERBOSE:
    x_labels = [0, 1]
    x = [i for i in range(len(x_labels))]
    count_in_train = [y_train.tolist().count(label) / len(y_train) for label in x_labels]  #统计训练集占比
    count_in_val = [y_valid.tolist().count(label) / len(y_valid) for label in x_labels]  #统计验证集占比
    count_in_test = [y_test.tolist().count(label) / len(y_test) for label in x_labels]  #统计测试集占比
    plt.figure()
    plt.bar(x, count_in_train, width=0.3, label="train_set")
    plt.bar([i + 0.3 for i in x], count_in_val, width=0.3, label="val_set")
    plt.bar([i + 0.6 for i in x], count_in_test, width=0.3, label="test_set")
    plt.xticks([i + 0.3 for i in x], x_labels)
    plt.legend()
    plt.show()

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
 

比较训练集、验证集和测试集中不同类别的样本数量。这里我们使用matplotlib绘制不同数据集中不同类别在总数据量中的比例的柱状图。在绘制柱状图时，首先统计数据集中不同类别的数据占整个数据集的比例，得到count_in_train，然后通过plt.bar()绘制柱状图并使用plt.xticks()绘制横坐标，最后利用plt.legend()添加图例，利用plt.show()将图展示出来。

从下图中可以看出：数据集存在类别不平衡的问题，但是在训练集、验证集、测试集上的比例是差不多的。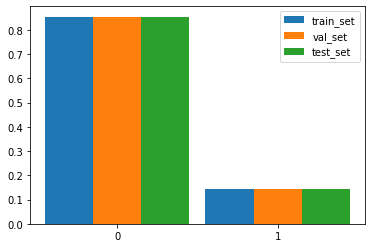

1.3 初始化模型输入

使用torch的nn.Embedding工具构造输入的特征和图

# 矩阵正则化
def normalize(mx):
    rowsum = np.array(mx.sum(1)) + 0.01
    r_inv = np.power(rowsum, -1).flatten()
    r_inv[np.isinf(r_inv)] = 0.
    r_mat_inv = sp.diags(r_inv)
    mx = r_mat_inv.dot(mx)
    return mx
# 查看是否有可用的cuda
cuda = not no_cuda and torch.cuda.is_available()
features = nn.Embedding(feat_data.shape[0], feat_data.shape[1])
feat_data = normalize(feat_data)
features.weight = nn.Parameter(torch.FloatTensor(feat_data), requires_grad=False)
if cuda:
    features.cuda()
adj_lists = homo

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
 

2.自动加权GCN模型构建

2.1 构造模型单层结构

首先构建GCN的单层结构，需要定义forward()方式。先对邻居进行降采样；如果使用GCN方式进行聚合，则在邻接列表中加入自身，获取邻居的特征在整个特征矩阵中的位置；通过聚合邻居的方式，来更新节点的embedding。这里更详细的可以看paper描述。

下图算法1描述了在整个图上生成embedding的过程，其中：

• 图$\mathcal{G}=(\mathcal{V},\mathcal{E})$，$K$ 是网络层数，也代表每个顶点能够聚合的邻接点的跳数（因为每增加一层，可以聚合更远的一层邻居信息）
• $x_v,\forall v\in \mathcal{V}$表示节点$v$的属性（特征向量），并且作为输入
• $\left\{{\mathbf{h}}_u^{k-1},\forall u\in \mathcal{N}(v)\right\}$表示在$(k-1)$层中节点$v$的邻居节点$u$的embedding
• ${\mathbf{h}}_v^k,\forall v\in V$表示在第$k$层，节点$v$的特征表示
• $\mathcal{N}(v)$定义为邻居节点集合$$\{u\in v:(u,\mathcal{V})\in \mathcal{E}\}$$需要从中均匀采样出固定数量的节点做聚合，即GraphSAGE中每一层的节点邻居都是从上一层网络采样的，并不是所有邻居参与，并且采样后的邻居的size是固定的。${\mathbf{h}}_{\mathcal{N}(v)}^k$表示在第$k$层，节点$v$的所有邻居节点的特征表示。

敲黑板：
上图的4-5行是核心代码，介绍了卷积层操作：聚合与节点v相连的邻居（采样）k-1层的embedding，得到第k层邻居聚合特征 ${\mathbf{h}}_{\mathcal{N}(v)}^k$，与节点v第k-1层 embedding ${\mathbf{h}}_{\mathcal{V}}^k$拼接，并通过全连接层转换，然后进入激活函数计算，得到节点v在第k层的embedding ${\mathbf{h}}_{\mathcal{V}}^k$。
第7行代码：通过除以矢量范数来标准化节点嵌入，以防止梯度爆炸。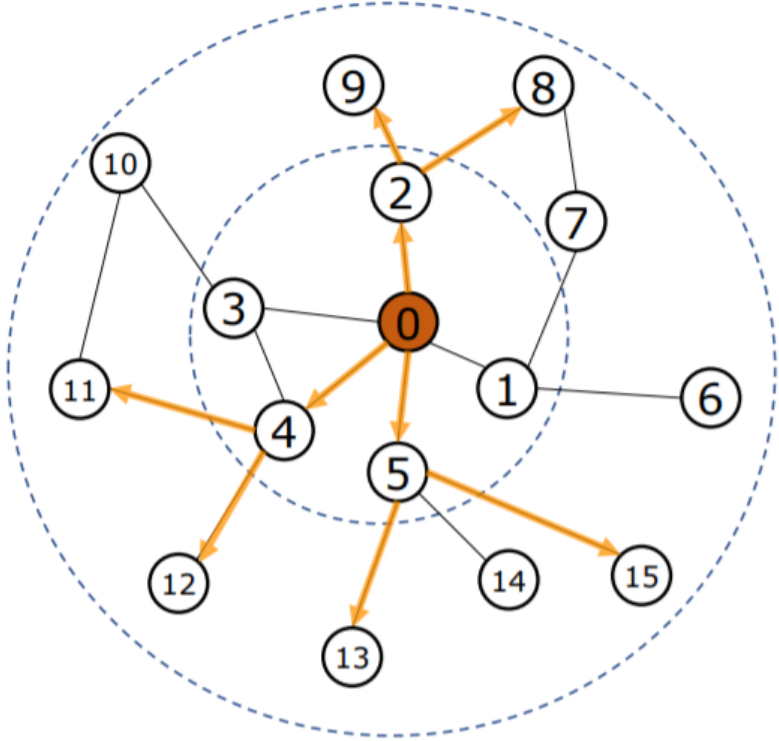

如上图的栗子进行采样，要预测 0 号节点，因此首先随机选择 0 号节点的一阶邻居 2、4、5，然后随机选择 2 号节点的一阶邻居 8、9，对于4、5号节点也是类似。

# 使用PyTorch的接口构建模型
import torch.nn.functional as F
from torch.autograd import Variable
# 构建图神经网络的单层模型
class MeanAggregator(nn.Module):
    # 初始化单层模型
    def __init__(self, features, cuda=False, gcn=True):
        super(MeanAggregator, self).__init__()
        self.features = features
        self.cuda = cuda
        self.gcn = gcn
    # 定义前递函数，输入节点和其邻接列表
    def forward(self, nodes, to_neighs, num_sample=10):
        _set = set
        # 对邻居进行降采样
        if not num_sample is None:
            _sample = random.sample
            samp_neighs = [_set(_sample(to_neigh,
                                        num_sample,
                                        )) if len(to_neigh) >= num_sample else to_neigh for to_neigh in to_neighs]
        else:
            samp_neighs = to_neighs
        # 如果使用GCN方式进行聚合，则在邻接列表中加入自身
        if self.gcn:
            samp_neighs = [samp_neigh.union(set([int(nodes[i])])) for i, samp_neigh in enumerate(samp_neighs)]
        # 计算无重复的邻居列表
        unique_nodes_list = list(set.union(*samp_neighs))
        unique_nodes = {n: i for i, n in enumerate(unique_nodes_list)}
        # 获取邻居的特征在整个特征矩阵中的位置
        mask = Variable(torch.zeros(len(samp_neighs), len(unique_nodes)))
        column_indices = [unique_nodes[n] for samp_neigh in samp_neighs for n in samp_neigh]
        row_indices = [i for i in range(len(samp_neighs)) for j in range(len(samp_neighs[i]))]
        mask[row_indices, column_indices] = 1
        if self.cuda:
            mask = mask.cuda()
        num_neigh = mask.sum(1, keepdim=True)
        mask = mask.div(num_neigh)
        # 通过聚合邻居的方式，更新节点的表示
        if self.cuda:
            embed_matrix = self.features(torch.LongTensor(unique_nodes_list).cuda())
        else:
            embed_matrix = self.features(torch.LongTensor(unique_nodes_list))
        to_feats = mask.mm(embed_matrix)
        return to_feats

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
 

2.2 构建自动加权模块

自动调节节点的权重，其中节点的权重不会低于某个阈值：为每次当前训练的batch的节点分配权重，将过小的权重修正到至少为某个阈值eps。

# 构建自动加权模块
def auto_weight(bsize, eps=0.0):
    # 为当前训练batch的节点分配权重
    ex_weight = torch.randn([bsize]) #mean=0.0, stddev=1.0
    # 将过小的权重修正到至少为某个阈值eps,这里阈值设为0
    ex_weight_eps = torch.full([bsize], eps)
    # 对权重进行归一化，使其和为1
    ex_weight_plus = torch.max(ex_weight, ex_weight_eps)
    ex_weight_sum = torch.full([bsize], torch.sum(ex_weight_plus))
    ex_weight_norm = ex_weight_plus / ex_weight_sum
    return ex_weight_norm

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

2.3 构建自动加权模型整体结构

在计算节点的loss时使用加权的方式。

# 构建图编码器的结构
class Encoder(nn.Module):
    # 定义图编码器的结构和参数
    def __init__(self, features, feature_dim,
                 embed_dim, adj_lists, aggregator,
                 num_sample=10,
                 base_model=None, gcn=True, cuda=False,
                 feature_transform=False):
        super(Encoder, self).__init__()

        self.features = features
        self.feat_dim = feature_dim
        self.adj_lists = adj_lists
        self.aggregator = aggregator
        self.num_sample = num_sample
        if base_model != None:
            self.base_model = base_model
        self.gcn = gcn
        self.embed_dim = embed_dim
        self.cuda = cuda
        self.aggregator.cuda = cuda
        self.weight = nn.Parameter(
            torch.FloatTensor(embed_dim, self.feat_dim if self.gcn else 2 * self.feat_dim))
        init.xavier_uniform_(self.weight)
    # 定义前递函数，更新节点的表示
    def forward(self, nodes):
        neigh_feats = self.aggregator.forward(nodes, [self.adj_lists[int(node)] for node in nodes],
                                              self.num_sample)

        if isinstance(nodes, list):
            if cuda:
                index = torch.LongTensor(nodes).cuda()
            else:
                index = torch.LongTensor(nodes)
        else:
            index = nodes

        if not self.gcn:
            if self.cuda:
                self_feats = self.features(index)
            else:
                self_feats = self.features(index)
            combined = torch.cat((self_feats, neigh_feats), dim=1)
        else:
            combined = neigh_feats
        combined = F.relu(self.weight.mm(combined.t()))
        return combined

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
 

构建GraphSAGE模型，定义前递函数，通过将学习到的节点表示与参数矩阵相乘，计算节点的分数。

# 构建图神经网络整体模型
class GraphSage(nn.Module):
    # 设定图神经网络的结构和参数
    def __init__(self, num_classes, enc):
        super(GraphSage, self).__init__()
        self.enc = enc
        self.xent = nn.CrossEntropyLoss()
        self.weight = nn.Parameter(torch.FloatTensor(num_classes, enc.embed_dim))
        init.xavier_uniform_(self.weight)
    # 定义前递函数，通过将学习到的节点表示与参数矩阵相乘，计算节点的分数
    def forward(self, nodes):
        embeds = self.enc(nodes)
        scores = self.weight.mm(embeds)
        return scores.t()
    # 计算节点的预测类别分数
    def to_prob(self, nodes):
        pos_scores = torch.sigmoid(self.forward(nodes))
        return pos_scores
    # 计算自动加权后的分类损失
    def loss(self, nodes, labels):
        scores = self.forward(nodes)
        # 对损失进行自动加权
        ex_weights = auto_weight(len(labels),0)
        loss = self.xent(scores, labels.squeeze())
        weighted_loss = torch.sum(torch.mul(loss, ex_weights))
        return weighted_loss
# 使用上面构建的图神经网络模型实际搭建本次使用的模型gnn_model
agg1 = MeanAggregator(features, cuda=cuda)
enc1 = Encoder(features, feat_data.shape[1], emb_size, adj_lists, agg1, gcn=True, cuda=cuda)
enc1.num_samples = 5
gnn_model = GraphSage(2, enc1)
if cuda:
    gnn_model.cuda()
# 设定优化器参数
optimizer = torch.optim.Adam(filter(lambda p: p.requires_grad, gnn_model.parameters()), lr=lr, weight_decay=lambda_2)
times = []
performance_log = []

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
 

3.反洗钱识别模型训练与测试

使用自动加权GCN做为分类模型，并使用默认参数。

3.1 定义测试函数

使用F1、ACC、AUC作为测试指标

# 设计评估指标和评估函数
def test_sage(test_cases, labels, model, batch_size):
    test_batch_num = int(len(test_cases) / batch_size) + 1
    f1_gnn = 0.0
    acc_gnn = 0.0
    recall_gnn = 0.0
    gnn_list = []
    # 对每一个测试batch进行遍历
    for iteration in range(test_batch_num):
        i_start = iteration * batch_size
        i_end = min((iteration + 1) * batch_size, len(test_cases))
        batch_nodes = test_cases[i_start:i_end]
        batch_label = labels[i_start:i_end]
        gnn_prob = model.to_prob(batch_nodes)
        # 计算F1-macro分数
        f1_gnn += f1_score(batch_label, gnn_prob.data.cpu().numpy().argmax(axis=1), average="macro")
        # 计算准确度分数
        acc_gnn += accuracy_score(batch_label, gnn_prob.data.cpu().numpy().argmax(axis=1))
        # 记录每个节点被分为正类的概率,用来计算AUC分数
        gnn_list.extend(gnn_prob.data.cpu().numpy()[:, 1].tolist())
    # 计算AUC分数
    auc_gnn = roc_auc_score(labels, np.array(gnn_list))
    print(f"GNN F1: {f1_gnn / test_batch_num:.4f}")
    print(f"GNN Accuracy: {acc_gnn / test_batch_num:.4f}")
    print(f"GNN auc: {auc_gnn:.4f}")

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
 

3.2 设计对负样本的随机降采样

减少由于负类过多导致的分类器bias

# 对负样本随机降采样,scale是采样后的负类与正类的比例,这里采用1:1
def undersample(pos_nodes, neg_nodes, scale=1):
    aux_nodes = cp.deepcopy(neg_nodes)
    aux_nodes = random.sample(aux_nodes, k=int(len(pos_nodes)*scale))
    # 得到训练batch的节点集合
    batch_nodes = pos_nodes + aux_nodes

    return batch_nodes

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

3.3 进行训练和测试

开始对模型的训练，当模型达到设定的测试epoch时，进行测试。

# 训练模型

for epoch in range(num_epochs):
    # 在每个epoch中,随机降采样负类样本
    sampled_idx_train = undersample(train_pos, train_neg, scale=1)
    random.shuffle(sampled_idx_train)
    num_batches = int(len(sampled_idx_train) / batch_size) + 1

    loss = 0.0
    epoch_time = 0

    # mini-batch训练
    for batch in range(num_batches):
        start_time = time.time()
        i_start = batch * batch_size
        i_end = min((batch + 1) * batch_size, len(sampled_idx_train))
        # 获取降采样后的节点和其标签
        batch_nodes = sampled_idx_train[i_start:i_end]
        batch_label = labels[np.array(batch_nodes)]
        optimizer.zero_grad()
        # 计算模型输出和分类损失
        if cuda:
            loss = gnn_model.loss(batch_nodes, Variable(torch.cuda.LongTensor(batch_label)))
        else:
            loss = gnn_model.loss(batch_nodes, Variable(torch.LongTensor(batch_label)))
        # 用优化器进行梯度回传.更新模型参数
        loss.backward()
        optimizer.step()
        # 记录当前batch的训练时间和分类损失
        end_time = time.time()
        epoch_time += end_time - start_time
        loss += loss.item()
    # 输出当前batch的详细情况
    if VERBOSE:
        print(f'Epoch: {epoch}, loss: {loss.item() / num_batches}, time: {epoch_time}s')
    
    # 在测试集上测试模型的表现
    if epoch % test_epochs == 0:
        test_sage(idx_test, y_test, gnn_model, batch_size)       

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
 

4 模型结果

训练31个epoch得到的结果：

Epoch: 30, loss: 0.1829193433125814, time: 0.043320417404174805s
GNN F1: 0.7023
GNN Accuracy: 0.8376
GNN auc: 0.8165

  

 

  
1
  
2
  
3
  
4
 

5.模型部署

该模型可以用云端的方式部署在服务器上。

6.指标监测系统

实际生产中，需要关注行为数据的分布，控制节点自动加权的最低阈值在合理范围内。

7.优化思路

• 数据
  • 数据清洗：对负类节点的随机降采样可以对节点的特征分布进行聚类，将节点距离聚类中心的距离作为标准之一
• 模型
  • 参数：学习率、正则项、自动加权阈值可以调整
  • 可扩展性：根据输入的图数据的性质，优化底层图神经网络，如换成图注意力神经网络等其他图神经网络模型

Reference

[1] https://github.com/YingtongDou/CARE-GNN/blob/master/model.py
[2] https://stellargraph.readthedocs.io/en/latest/demos/embeddings/graphsage-unsupervised-sampler-embeddings.html

文章来源: andyguo.blog.csdn.net，作者：山顶夕景，版权归原作者所有，如需转载，请联系作者。

原文链接：andyguo.blog.csdn.net/article/details/126681519