2025-12-09:分割字符串。用go语言,从索引 0 开始,对字符串按顺序切出一段子串。 逐字符向右扩展当前子串:如果它与之
【摘要】 2025-12-09:分割字符串。用go语言,从索引 0 开始,对字符串按顺序切出一段子串。逐字符向右扩展当前子串:如果它与之前已经产生过的任一子串相同,就继续加字符;一旦变成一个此前未出现过的新子串,就停止扩展。把这个新子串加入结果集合并记为已出现,然后从下一个位置继续重复上述过程,直至处理完整个字符串。最终返回一个数组 segments,按生成顺序记录所有得到的子串(segments[i...
2025-12-09:分割字符串。用go语言,从索引 0 开始,对字符串按顺序切出一段子串。
逐字符向右扩展当前子串:如果它与之前已经产生过的任一子串相同,就继续加字符;一旦变成一个此前未出现过的新子串,就停止扩展。
把这个新子串加入结果集合并记为已出现,然后从下一个位置继续重复上述过程,直至处理完整个字符串。
最终返回一个数组 segments,按生成顺序记录所有得到的子串(segments[i] 表示第 i 个生成的片段)。
1 <= s.length <= 100000。
s 仅包含小写英文字母。
输入: s = “abbccccd”。
输出: [“a”,“b”,“bc”,“c”,“cc”,“d”]。
解释:
| 下标 | 添加后的段 | 已经出现过的段 | 当前段是否已经出现过? | 新段 | 更新后已经出现过的段 |
|---|---|---|---|---|---|
| 0 | “a” | [] | 否 | “” | [“a”] |
| 1 | “b” | [“a”] | 否 | “” | [“a”, “b”] |
| 2 | “b” | [“a”, “b”] | 是 | “b” | [“a”, “b”] |
| 3 | “bc” | [“a”, “b”] | 否 | “” | [“a”, “b”, “bc”] |
| 4 | “c” | [“a”, “b”, “bc”] | 否 | “” | [“a”, “b”, “bc”, “c”] |
| 5 | “c” | [“a”, “b”, “bc”, “c”] | 是 | “c” | [“a”, “b”, “bc”, “c”] |
| 6 | “cc” | [“a”, “b”, “bc”, “c”] | 否 | “” | [“a”, “b”, “bc”, “c”, “cc”] |
| 7 | “d” | [“a”, “b”, “bc”, “c”, “cc”] | 否 | “” | [“a”, “b”, “bc”, “c”, “cc”, “d”] |
因此,最终输出为 [“a”, “b”, “bc”, “c”, “cc”, “d”]。
题目来自力扣3597。
📝 算法步骤分解
我们以输入字符串 s = "abbccccd" 为例,结合你提供的表格进行说明。算法维护两个关键数据结构:一个用于记录结果的字符串切片 segments,和一个用于记录已出现子串的集合 seen(在代码中是一个 map[string]bool)。
-
初始化
- 指针
i置为0,指向当前子串的起始位置。 segments和seen均为空。
- 指针
-
外层循环:处理整个字符串
- 只要
i未到达字符串末尾,就开启一轮新的子串分割。
- 只要
-
内层循环:确定当前子串的结束位置
- 指针
j从i开始,逐步向右移动,尝试扩展当前子串s[i:j+1]。 - 在每一步扩展中,检查当前子串
s[i:j+1]是否存在于seen集合中:- 如果存在:说明这个子串之前已经出现过了,不符合“新子串”的要求。于是
j继续向右移动一位,尝试添加一个字符,形成一个更长的子串,希望这个更长的子串是新的。 - 如果不存在:说明找到了一个全新的子串。此时,内层循环结束。
- 如果存在:说明这个子串之前已经出现过了,不符合“新子串”的要求。于是
- 指针
-
分割与记录
- 将最终确定的、全新的子串
s[i:j+1]追加到结果切片segments的末尾。 - 同时,将这个新子串加入到
seen集合中,标记为已出现。 - 将指针
i更新为j + 1,从而开始下一轮的分割。
- 将最终确定的、全新的子串
-
循环直至结束
- 重复步骤2-4,直到整个字符串被处理完毕。
结合例子 "abbccccd" 的关键过程解读:
- 第一段:从
"a"开始。"a"不在seen中,直接分割,得到["a"]。 - 第二段:从
"b"开始。"b"不在seen中,直接分割,得到["a", "b"]。 - 第三段:从第二个字符
"b"开始。单字符"b"已经在seen中,因此必须扩展为"bc"。"bc"是新的,所以分割,得到["a", "b", "bc"]。 - 后续过程:遵循同样的规则。例如,单个
"c"出现时,因为之前"bc"中已包含"c"导致"c"已存在?这里需要仔细看:当算法处理到第四个字符'c'(下标3)时,seen里是["a", "b", "bc"],单字符"c"是新的,所以此时会分割出"c"。之后再遇到单个'c'时,因为它已存在,就需要扩展成"cc"才成为新子串。
这个过程确保了每个被记录的片段都是在其被创建的瞬间是独一无二的。
⚙️ 复杂度分析
总的额外空间复杂度
- O(n²),其中
n是字符串s的长度。 - 原因分析:
seen集合:在最坏情况下,算法可能会产生 O(n) 个不同的子串。然而,这些子串本身可能很长。例如,当字符串由同一个字符组成(如"aaaa")时,可能会产生"a","aa","aaa","aaaa"等子串。存储这些子串所需的总空间是 1 + 2 + 3 + … + n = O(n²)。segments切片:它存储的是对原字符串的引用或子串的拷贝(取决于Go语言的字符串实现)。在最坏情况下,它也需要存储 O(n) 个子串,总空间同样可能达到 O(n²)。
因此,空间复杂度主要由存储所有唯一子串的成本决定,为 O(n²)。
总的时间复杂度
- O(n³)。
- 原因分析:
- 外层循环:最多执行 O(n) 次,因为每次至少分割出一个字符。
- 内层循环:指针
j每次从i开始向右移动,最坏情况下需要扫描 O(n) 个字符。 - 子串检查:对于每个
s[i:j+1],都需要在seen集合(哈希表)中检查其是否存在。哈希表查找的平均时间复杂度是 O(k),其中k是键的长度。在这里,键就是子串s[i:j+1],其长度最大为 O(n)。
将这三者相乘,最坏情况下的总时间复杂度是 O(n) * O(n) * O(n) = O(n³)。
希望这个分步骤的详解和复杂度分析能帮助你完全理解这个算法!
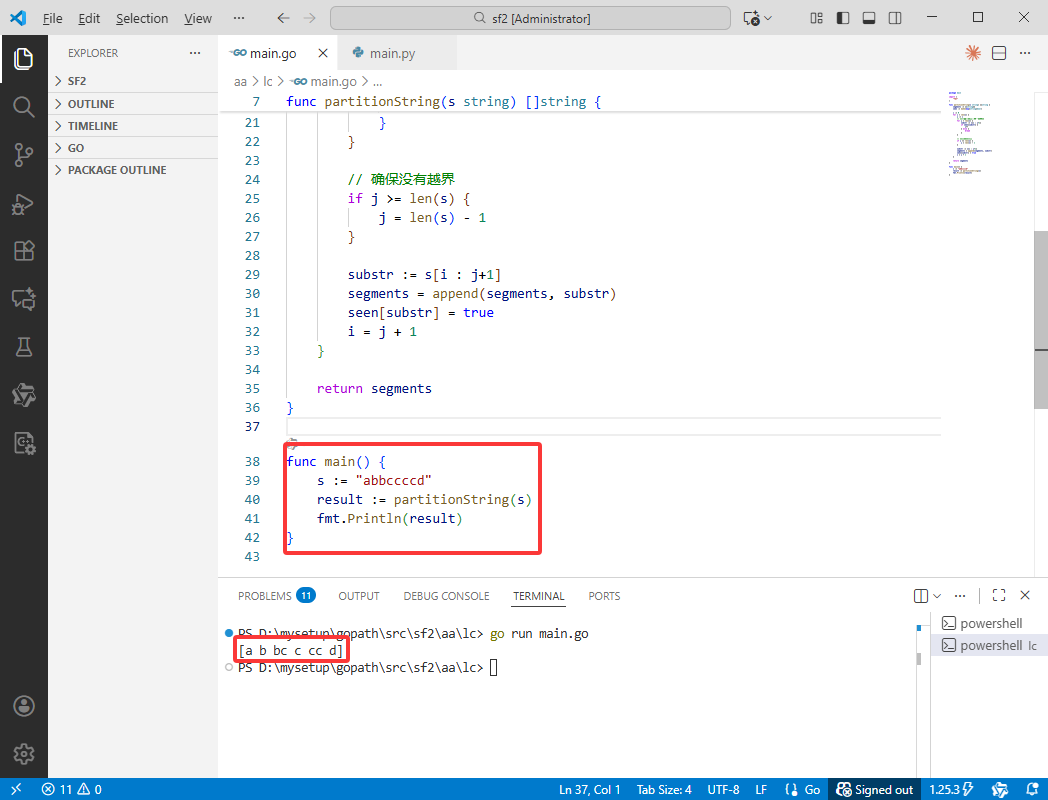
Go完整代码如下:
package main
import (
"fmt"
)
func partitionString(s string) []string {
segments := []string{}
seen := make(map[string]bool)
i := 0
for i < len(s) {
j := i
// 寻找最小的未出现过的子串
for j < len(s) {
substr := s[i : j+1]
if seen[substr] {
j++
} else {
break
}
}
// 确保没有越界
if j >= len(s) {
j = len(s) - 1
}
substr := s[i : j+1]
segments = append(segments, substr)
seen[substr] = true
i = j + 1
}
return segments
}
func main() {
s := "abbccccd"
result := partitionString(s)
fmt.Println(result)
}
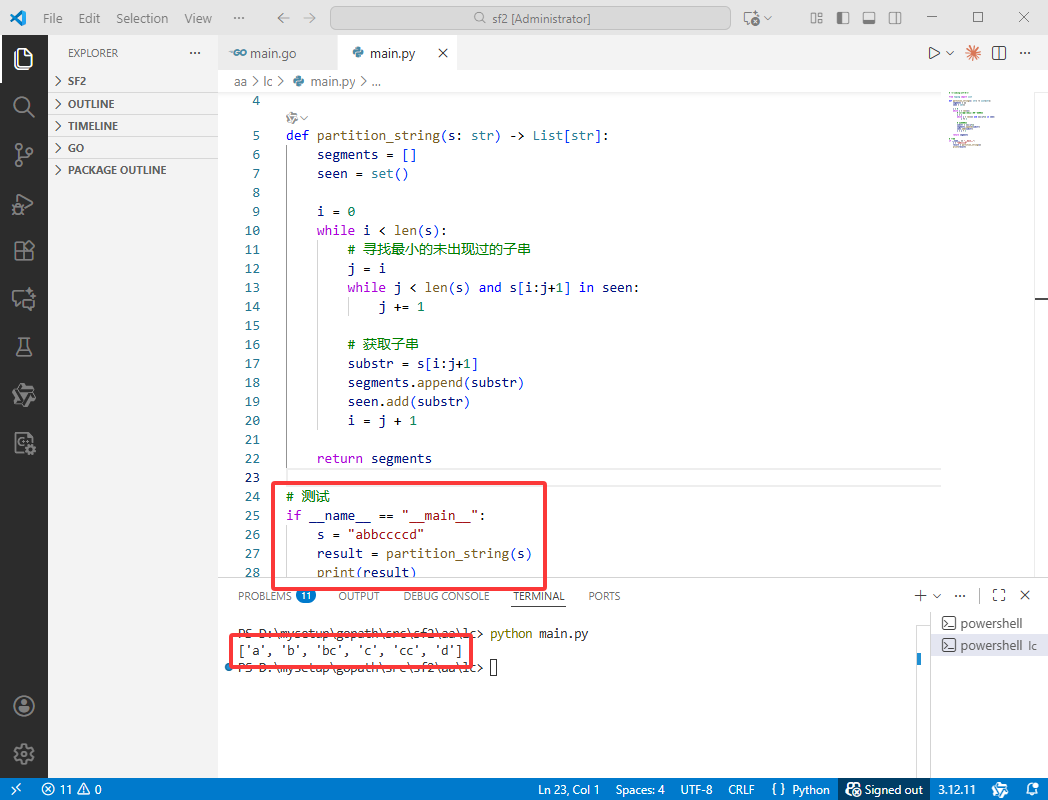
Python完整代码如下:
# -*-coding:utf-8-*-
from typing import List
def partition_string(s: str) -> List[str]:
segments = []
seen = set()
i = 0
while i < len(s):
# 寻找最小的未出现过的子串
j = i
while j < len(s) and s[i:j+1] in seen:
j += 1
# 获取子串
substr = s[i:j+1]
segments.append(substr)
seen.add(substr)
i = j + 1
return segments
# 测试
if __name__ == "__main__":
s = "abbccccd"
result = partition_string(s)
print(result)
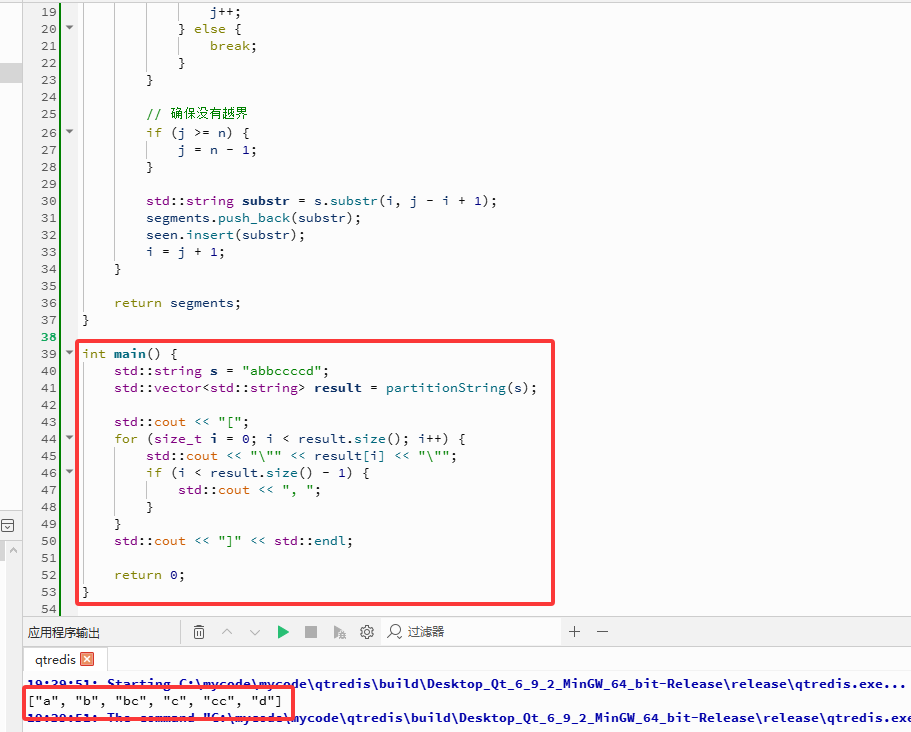
C++完整代码如下:
#include <iostream>
#include <vector>
#include <string>
#include <unordered_set>
std::vector<std::string> partitionString(const std::string& s) {
std::vector<std::string> segments;
std::unordered_set<std::string> seen;
int i = 0;
int n = s.length();
while (i < n) {
int j = i;
// 寻找最小的未出现过的子串
while (j < n) {
std::string substr = s.substr(i, j - i + 1);
if (seen.find(substr) != seen.end()) {
j++;
} else {
break;
}
}
// 确保没有越界
if (j >= n) {
j = n - 1;
}
std::string substr = s.substr(i, j - i + 1);
segments.push_back(substr);
seen.insert(substr);
i = j + 1;
}
return segments;
}
int main() {
std::string s = "abbccccd";
std::vector<std::string> result = partitionString(s);
std::cout << "[";
for (size_t i = 0; i < result.size(); i++) {
std::cout << "\"" << result[i] << "\"";
if (i < result.size() - 1) {
std::cout << ", ";
}
}
std::cout << "]" << std::endl;
return 0;
}
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)