@toc

一：根据二叉树创建字符串

• 题目介绍：（题目链接）
  
• 代码：

class Solution {
public:
    string tree2str(TreeNode* root) {
         string ss;
         treecopy(root,ss);
         return ss;
    }
    void treecopy(TreeNode* root,string& str) //传引用减少构造
    {
        if(root == nullptr)
        return ;

        str+= to_string(root->val);

        if(root->left || root -> right)
        {
            str+="(";
           treecopy(root->left,str);
            str+=")";
        }

        if(root->right)
    {
        str+="(";
           treecopy(root->right,str);
            str+=")";
    }
    }
};

• 思路：

利用的是前序遍历

• 注意：

1. 左子树和右子树的判断条件 ： 1. if(root->left || root -> right) （假如左子树或者右子树不为空，则执行左） 2. if(root->right) （只有当右子树不为空时，执行右分支）
2. to_string的利用
3. void treecopy(TreeNode* root,string& str) （传引用减少构造）

二：二叉树层序遍历

题目描述：（题目链接）

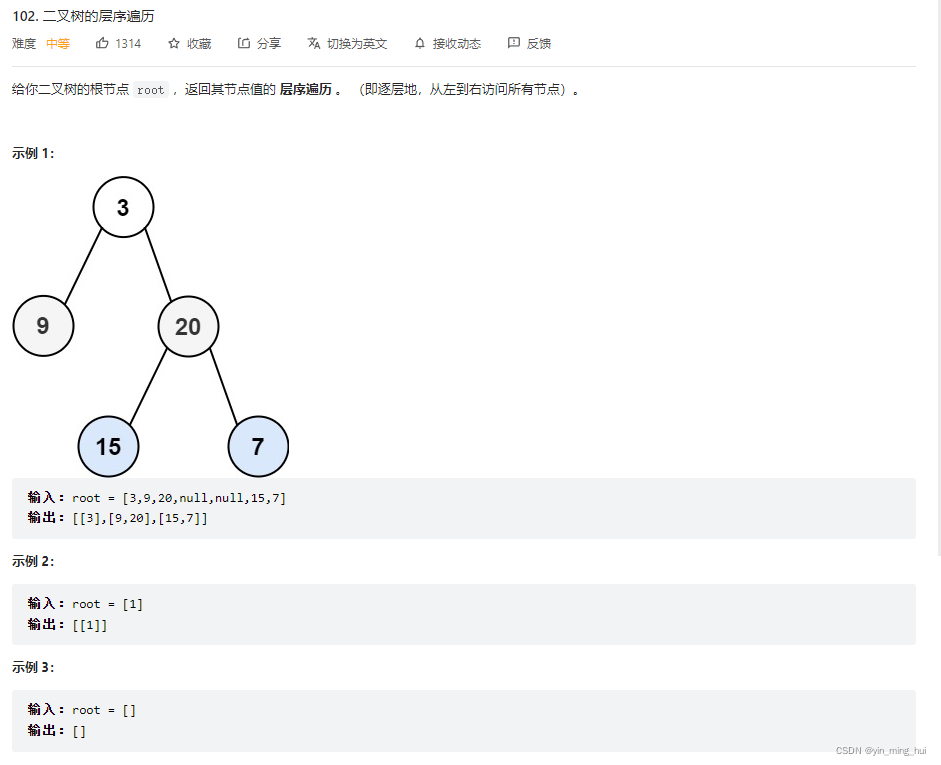
• 方法一：

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> vv;
         if(root ==nullptr)
         return  vv;

         queue<TreeNode*> q;
         q.push(root);
         int numsize =1;
         while(!q.empty())
         {
             //一层一层的遍历
             vector<int> v;
           for(int i=0;i<numsize;i++)
           {
               TreeNode* cur = q.front();
               q.pop();
               v.push_back(cur->val);

               if(cur->left)
               q.push(cur->left);
               if(cur->right)
               q.push(cur->right);
           }
           vv.push_back(v);
           numsize = q.size();
           }
           return vv;

• 思路：

1. 记录当前层数的个数， 一层一层的遍历
2. 利用了队列先进先出的特性

• 注意事项：

1. 注意队列函数的使用 ： q.front() 取出队头的数据
   q,back() 取队尾的数据
   （需要注意是的栈只能取队尾的数据，不能取对头的）
2. 注意for循环的使用和numsize的更新，for(int i=0;i<numsize;i++)， numsize = q.size();

• 方法二：

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> vv;
         if(root ==nullptr)
         return  vv;

         queue<TreeNode*> q;
         q.push(root);
         int numsize =1;
         while(!q.empty())
         {
           
             TreeNode* cur = q.front(); //取出队列的头
             v.push_back(cur->val);
             q.pop();
             numsize--;

             if(cur->left)
             q.push(cur->left);
             if(cur->right)
             q.push(cur->right);

             if(numsize==0)
             {
                 vector<int> tem =v;
                 v.clear();
                 vv.push_back(tem);
                 numsize = q.size();
             }
         }
         return vv;
    }
};

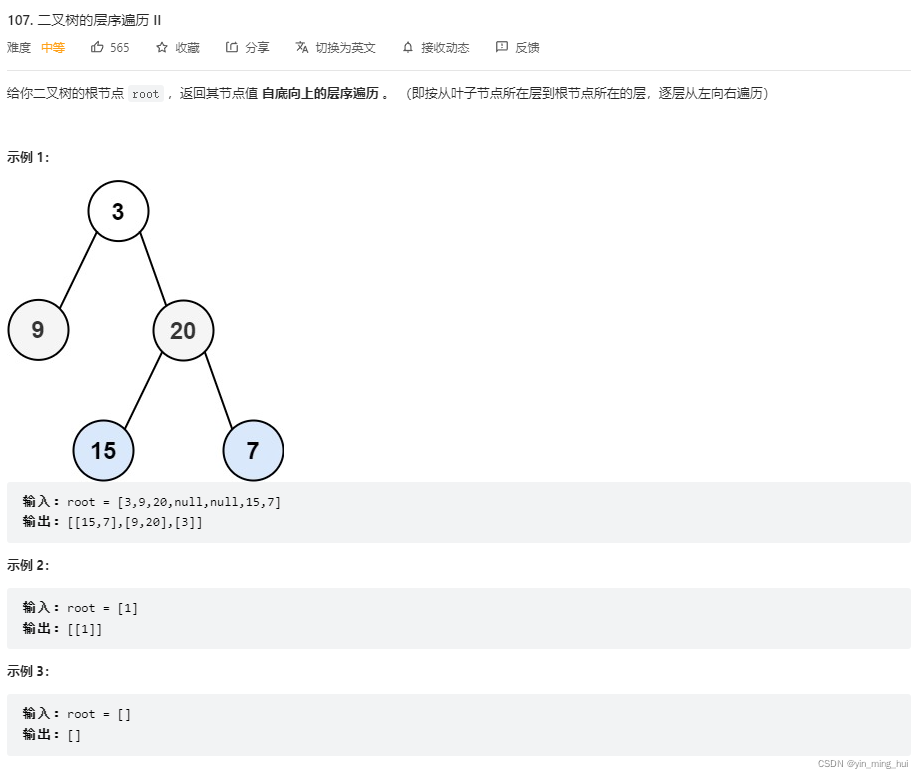
三：二叉树的层序遍历 II

• 题目描述： （题目链接）
  
• 代码：

class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
         vector<vector<int>> vv;
         if(root ==nullptr)
         return  vv;

         queue<TreeNode*> q;
         q.push(root);
         int numsize =1;
         while(!q.empty())
         {
             //一层一层的遍历
             vector<int> v;
           for(int i=0;i<numsize;i++)
           {
               TreeNode* cur = q.front();
               q.pop();
               v.push_back(cur->val);

               if(cur->left)
               q.push(cur->left);
               if(cur->right)
               q.push(cur->right);
           }
           numsize =q.size();
           vv.push_back(v);
         }
         reverse(vv.begin(),vv.end());
         return vv;
    }
};

• 思路：

reverse一下就得到了

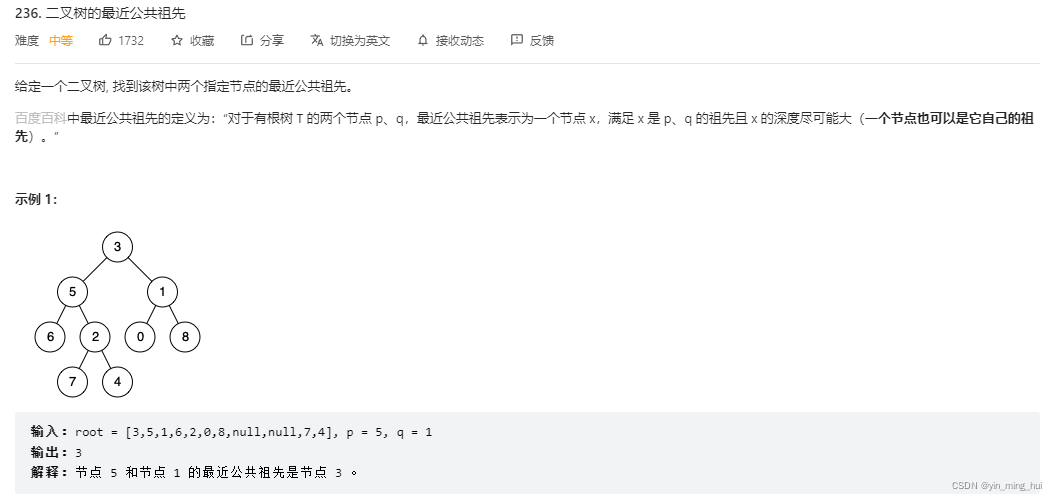
四：二叉树的最近公共祖先

• 题目描述： 题目链接
  
• 方法一：

class Solution {
public:
bool find(TreeNode* root, TreeNode* p)
{
    if(root==nullptr)
    return false;

    if(root==p)
    return true;

     return find(root->right,p) ||  find(root->left,p);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //特殊情况
        if(root== p || root == q)
        return root;

        bool IsRightp=find(root->right,p);
        bool IsRightq=find(root->right,q);

        bool IsLeftp=!IsRightp;
         bool IsLeftq=!IsRightq;

         if(IsLeftp && IsLeftq)//全在左边
         {
            return  lowestCommonAncestor(root->left,p,q);
         }
         else if(IsRightp && IsRightq)//全在右边，就玩右边找
         {
             return lowestCommonAncestor(root->right,p,q);
         }
         else{
             return root;
         }
    }
};

• 思路：

1. 逻辑：找到第一个祖先， 有一个节点在祖先的左，有一个节点在祖先的右
2. .时间复杂度：N*N 算最坏的情况（第一次findN,第二次find N-1…），因为find的时间复杂度是O（N）

• 注意：

bool IsLeftp=!IsRightp;
bool IsLeftq=!IsRightq;
取反可以就不用再去递归左树了

• 方法二：

bool findpath(TreeNode* root,stack<TreeNode*>& st,TreeNode* p)
{
      if(root==nullptr)
      return false;

      st.push(root); //先将root 入进栈
      if(root==p) //找到了
    { 
        return true;
    }

    //往左边找
    if(findpath(root->left,st,p)) 
    {
        return true; //左边找到了
    }

      //往右边找
    if(findpath(root->right,st,p)) 
    {
        return true; //右边找到了
    }

     //左右子树都没找到
     st.pop();
     return false;
}
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack<TreeNode*> stp,stq;
       findpath(root,stp,p);
       findpath(root,stq,q);
       int psize = stp.size();
       int qsize = stq.size();

       int max = psize >qsize? psize : qsize;
       int min = psize+qsize-max;

       stack<TreeNode*>* maxst =  max== psize? &stp : &stq;
       stack<TreeNode*>* minst =  max== psize? &stq : &stp; //找到长度大的和长度小的
       
       int  size = max - min;
       while(size--)
       {
           maxst->pop();
       }
       while(maxst->top()!=minst->top())
       {
           maxst->pop();
           minst->pop();
       }
       return maxst->top();
       }
       };

• 思路：
  1. 找到p，q的路径
  2. 他们两个路径的交点就是共同祖先
  3. 两个栈交点的问题 可以理解为 链表交点问题来解决
  4. 时间复杂度为O（N）
• 注意：

1. 主要是findpath函数的实现，主要流程为：
   1. 先将root入进栈，再判断root是否为P,为p则找到了，return true
   2. 再判断左子树和右子树， if(findpath(root->left,st,p)) 假如左树找到了，则return true
   3. 假如左右子树都没找到，则pop出栈顶的元素

五：二叉树的前中后序遍历（非递归版）

前序

• 方法一：

通用法，前后中序都基于此思路

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
       //先将左树全部入栈，再出，入右
       stack<TreeNode*> st;
       vector<int> v;
         //流程法
     TreeNode* cur =root; //要访问的树
     while(cur || !st.empty())
     {
         while(cur) //一直往左入
         {
             v.push_back(cur->val);
             st.push(cur);
             cur = cur->left;
         }
         //左边入完了
         TreeNode* tem= st.top();
         st.pop();
         cur = tem->right; //左数完了，再去入右树
         }
       return v;
    }
};

• 思路：

1. 先将左子树入栈，边入边push_back
2. 左边入完了，再将本节点pop，入右树

• 注意：

1. 注意判断条件： while(cur || !st.empty()) ，当本节点不为空或者栈不为空的时候，进循环
2. TreeNode* tem= st.top(); //先将栈顶节点pop掉，因为已经push_back了
   st.pop();
   cur = tem->right; //左数完了，再去入右树

• 方法二：

简洁法

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
       //先将左树全部入栈，再出，入右
       stack<TreeNode*> st;
       vector<int> v;
       //简洁法
       if(root==nullptr)
       return v;
       st.push(root);
       while(!st.empty())
       {
           TreeNode* cur = st.top();
           st.pop();
           v.push_back(cur->val);

            if(cur->right)
                st.push(cur->right);
            if(cur->left)
            st.push(cur->left);
       }
    
       return v;
    }
};

中序

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
         stack<TreeNode*> st;
       vector<int> v;
     TreeNode* cur =root; //要访问的树
     while(cur || !st.empty())
     {
         while(cur) //一直往左入
         {
             
             st.push(cur);
             cur = cur->left;
         }
         //左边入完了
         TreeNode* tem= st.top();
         st.pop();
         v.push_back(tem->val); //左子树完了。访问根
         cur = tem->right;
     }
     return v;
    }
};

与前序不同的是 v.push_back(tem->val);的时机

后序

• 方法一：

将前序的结果反转即可得到后序的结果

• 方法二：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {      
        vector<int> v;
        if(root == nullptr)
        return v;

        stack<TreeNode* > st;
        TreeNode* cur = root;
        TreeNode* prev = nullptr;
        while(cur || !st.empty())
        {
            //先去左边循环
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }

             TreeNode* top = st.top(); //取栈顶的数据

             if(top->right == nullptr || top->right == prev)
             {
                 v.push_back(top->val);
                 st.pop();
                 prev =top;
             }
             else
             {
                cur = top->right;
             }
        }
        return v;
    }
};

• 思路：

1. 先入左数
2. 再取栈顶元素
3. 判断，假如（栈顶的右子树为空，或者 右子树为之前访问过的节点），就push_back，再pop，更新prev= 栈顶的元素
4. 如果假如不成立，则再取栈顶的左树去找

• 注意：

5. 注意 if(top->right == nullptr || top->right == prev) 判断条件

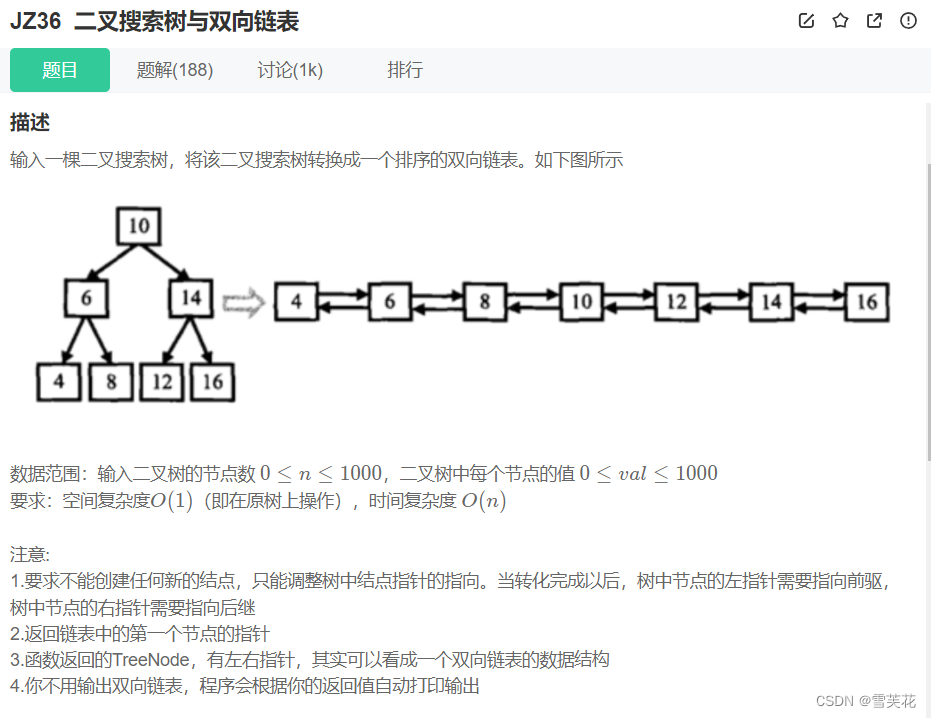
六：二叉搜索树与双向链表

• 题目描述：题目链接
  
• 代码：

class Solution {
public:
    void Inoder(TreeNode* cur,TreeNode*& prev)
    { 
         if(cur==nullptr)
             return;
        
        Inoder(cur->left,prev);
        
        cur->left = prev;
        if(prev)
            prev->right = cur;
        
        prev =cur;
         Inoder(cur->right,prev);
     }
    TreeNode* Convert(TreeNode* pRootOfTree) {
        if(pRootOfTree == nullptr)
            return pRootOfTree;
         TreeNode* prev = nullptr;
        
        Inoder(pRootOfTree,prev);
        
        TreeNode* head = pRootOfTree;
        while(head->left)
            head = head->left;
        
        return head;
    }
};

• 思路：

1. 利用中序遍历链接整颗树
2. 用一个prev指针指向前一个被访问的节点，然后当前节点的左子树指向 prev，假如prev不为空，prev的右子树指向当前节点，再更新pre。
3. 最后递归右子树

• 注意：

1. 注意prev要传引用，因为prev是要实时变化的
2. 链表的头不要格外的去记录，因为是双向链表，一直 往左就找到了

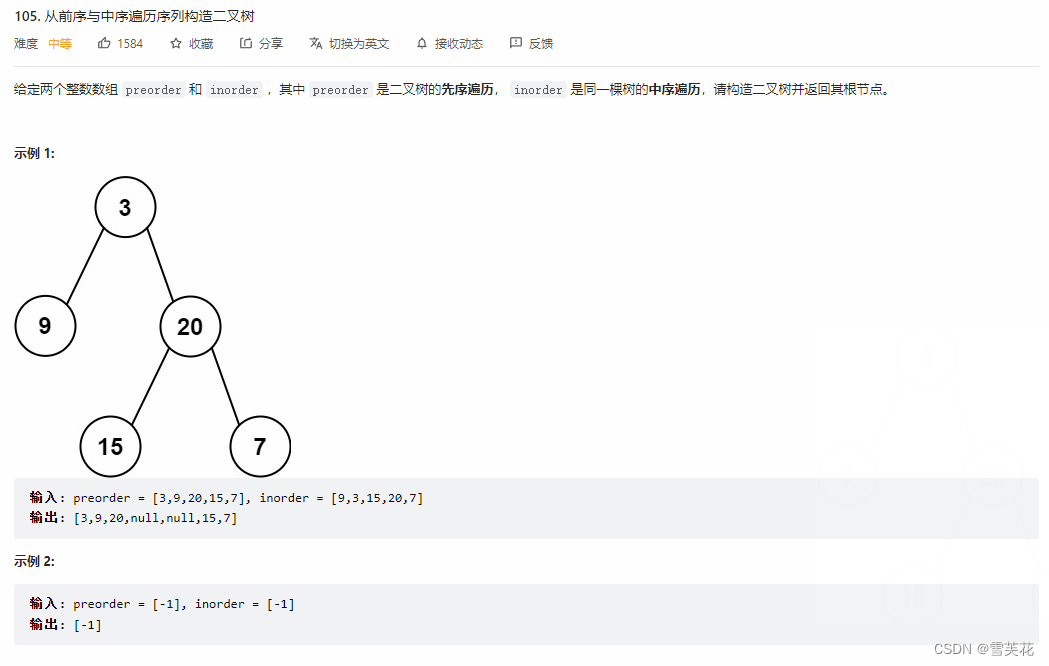
七：从前序与中序遍历序列构造二叉树

• 题目描述：题目链接
  
• 代码：

class Solution {
public:
     TreeNode* _buildTree(vector<int>& preorder,int& start,
     vector<int>& inorder,int left,int right)
     {
         if(left>right)
         return nullptr;

         //先由根构建节点
         TreeNode*  root = new TreeNode(preorder[start]);
         start++;
          
          //再利用中序去寻找左右子树的边界
          int preleft = left;
          int  i = root->val;
          while(left<=right)
          {
              if(i == inorder[left])
              {
                  break;
              }
              else
              left++;
          }
         root->left = _buildTree(preorder,start,inorder,preleft,left-1);
         root->right = _buildTree(preorder,start,inorder,left+1,right);

         return root;
     }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
              int start =0;
           return _buildTree(preorder,start,inorder,0,inorder.size()-1);
    }
};

• 思路：

利用前序找到根节点，再通过中序找到左右子树，从而构造出了一整颗树

• 注意：

1. 递归结束的条件：left>right
2. 注意start要传引用，因为要实时变化的。

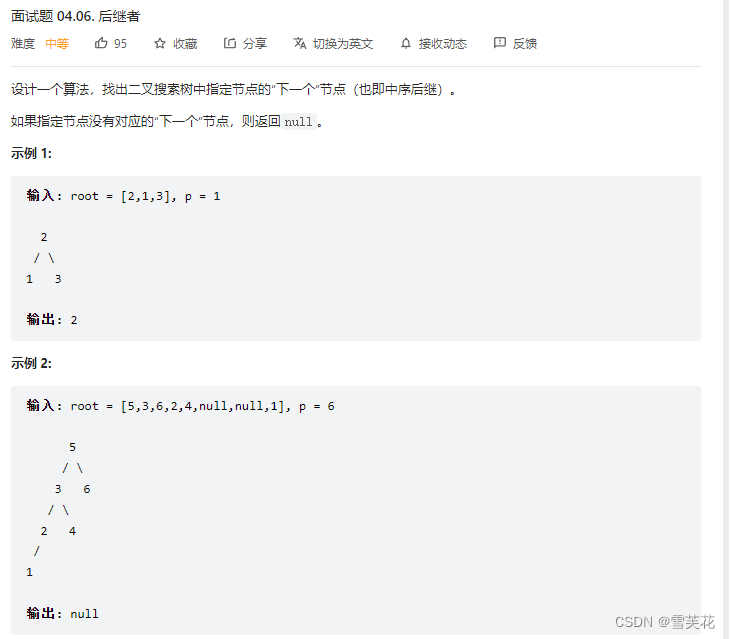
八：后继者

• 题目：题目链接
  
• 代码：

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        if(root==nullptr)
        return root;
        
        TreeNode*  cur = inorderSuccessor(root->left,p);
        if(cur != nullptr)
        return cur;

        if(root->val > p->val) //找到第一个大于P的值
        return root;

        return inorderSuccessor(root->right,p);
    }
};

• 思路：

中序找到第一个比p大的值就是后续

九：左子树之和

• 题目：（题目链接）
  

方法一：

• 代码：

class Solution {
public:
      void _sumOfLeftLeaves(TreeNode* root,int& sum){
          if(root == nullptr)
              return ;

              if(root->left!=nullptr && root->left->right==nullptr && root->left->left ==nullptr)
            sum += root->left->val;
            
            _sumOfLeftLeaves(root->left,sum);
            _sumOfLeftLeaves(root->right,sum);
      }
    int sumOfLeftLeaves(TreeNode* root) {
          int sum=0;
            _sumOfLeftLeaves(root,sum);
            return sum;
    } 
};

方法二：

• 代码：

class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
          int sum=0;
            _sumOfLeftLeaves(root,sum);
            return sum;

        if(root==nullptr)
        return 0;

        int leftsum = sumOfLeftLeaves(root->left);
        int rightsum = sumOfLeftLeaves(root->right);
        
        int tem =0;
        if(root->left!=nullptr && root->left->right==nullptr && root->left->left ==nullptr)
            tem = root->left->val;

            return leftsum+rightsum+tem;
    } 
};

• 思路：

递归去找左树上和右树上的左叶子节点，相加即可

• 注意：

特别要注意的是 左叶子节点的判断条件：root->left!=nullptr && root->left->right==nullptr && root->left->left ==nullptr

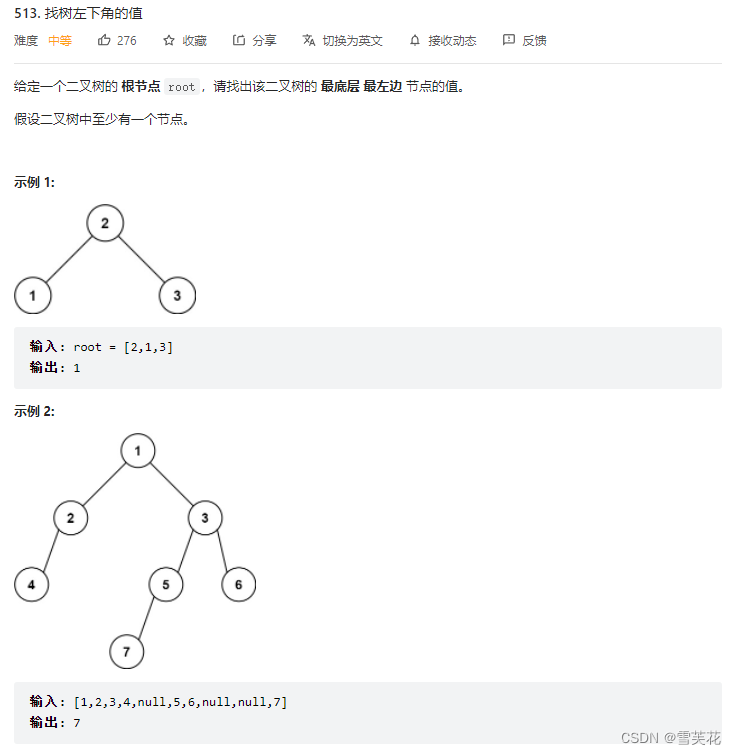
十：找树左下角的值

• 题目：（题目链接）
  

方法一：

层序遍历，找到最下面一层，最先从队列里出来的树

方法二：

• 代码：

class Solution {
public:
             int high=0,ret=0;//high 来记录当前最左节点的高度，ret记录答案
             void _findBottomLeftValue(TreeNode* root,int deep)
             {
                    if(root==nullptr)
                    return;

                    if(root->left==nullptr && root->right ==nullptr) //因为是前序遍历，所以同一高度，左树优先
                    {
                        if(deep > high)
                           {
                               ret=root->val;
                               high =deep;
                           }
                    }
                    if(root->left)  _findBottomLeftValue(root->left,deep+1);
                    if(root->right)  _findBottomLeftValue(root->right,deep+1);
             }
    int findBottomLeftValue(TreeNode* root) {
        ret =root->val;
         _findBottomLeftValue(root,high);
         return ret;
    }
};

• 思路：

1. 记录当前最左节点的高度，如果找到叶子节点的高度大于之前的，则该叶子节点为当前树的左下角
2. 因为是前序遍历，所以同一层的，左子树优先，所以可以求出左下角

• 注意：

注意全局变量的使用

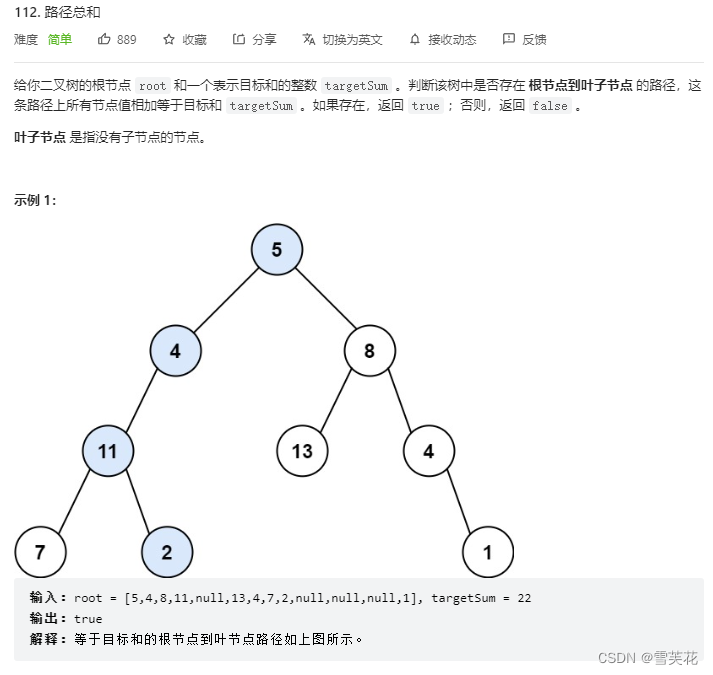
十一：路径总和

• 题目： （题目链接）
  
• 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        return _hasPathSum(root,0,targetSum);
    }
   bool  _hasPathSum(TreeNode* root, int curSum,int targetSum)
   {
       if(root==nullptr)
       {
         return false;
       }
       curSum+= root->val;
       if(root->left==nullptr && root->right==nullptr)
       {
           if(curSum == targetSum)
           return true;
           else
           return false;
       }
       if(_hasPathSum(root->left,curSum,targetSum))
       return true;

       if(_hasPathSum(root->right,curSum,targetSum))
       return true;

       return false;
   }
};

十二： 从前序与中序遍历序列构造二叉树

• 题目：（题目链接）
  

*代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
     TreeNode* _buildTree(vector<int>& preorder,int& start,
     vector<int>& inorder,int left,int right)
     {
         if(left>right)
         return nullptr;

         //先由根构建节点
         TreeNode*  root = new TreeNode(preorder[start]);
         start++;
          
          //再利用中序去寻找左右子树的边界
          int preleft = left;
          int  i = root->val;
          while(left<=right)
          {
              if(i == inorder[left])
              {
                  break;
              }
              else
              left++;
          }
         root->left = _buildTree(preorder,start,inorder,preleft,left-1);
         root->right = _buildTree(preorder,start,inorder,left+1,right);

         return root;
     }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
              int start =0;
           return _buildTree(preorder,start,inorder,0,inorder.size()-1);
    }
};

总结：

二叉树的oj题考察的主要是递归思想的运用和 非递归时，对整个递归流程的理解。
只有理解好递归的整个过程和思路，才能更好地学好二叉树

• 多写，多思考，多复习，多总结！！

• 持续更新中！！！