2025-12-10：相邻字符串之间的最长公共前缀。用go语言，给定一个字符串数组 words。对每个下标 i（0 到 words.length-1）按下面步骤处理并求得一个整数值：

1. 把数组中索引为 i 的元素删掉，得到一个长度为 n-1 的新数组（若原数组长度为 n）。

2. 在新数组中，把相邻的元素两两配对（即第 k 个和第 k+1 个），计算每一对从开头起相同的最长连续字符段的长度。

3. 在所有这些相邻对中取最大的那个长度作为该次删除的结果。如果删除后数组中没有相邻对（比如原来只有一个元素），或者所有相邻对的共同起始字符长度都是 0，则结果记为 0。

最终返回一个与原数组同样长度的整数数组 answer，其中 answer[i] 表示删除第 i 个元素后相邻对之间最大的“从头开始相同的连续前缀”的长度。

说明：字符串的前缀指的是从字符串开头连续截取的一段字符。

1 <= words.length <= 100000。

1 <= words[i].length <= 10000。

words[i] 仅由小写英文字母组成。

words[i] 的长度总和不超过 100000。

输入： words = [“jump”,“run”,“run”,“jump”,“run”]。

输出： [3,0,0,3,3]。

解释：

移除下标 0：

words 变为 [“run”, “run”, “jump”, “run”]

最长的相邻对是 [“run”, “run”]，其公共前缀为 “run”（长度为 3）

移除下标 1：

words 变为 [“jump”, “run”, “jump”, “run”]

没有相邻对有公共前缀（长度为 0）

移除下标 2：

words 变为 [“jump”, “run”, “jump”, “run”]

没有相邻对有公共前缀（长度为 0）

移除下标 3：

words 变为 [“jump”, “run”, “run”, “run”]

最长的相邻对是 [“run”, “run”]，其公共前缀为 “run”（长度为 3）

移除下标 4：

words 变为 [“jump”, “run”, “run”, “jump”]

最长的相邻对是 [“run”, “run”]，其公共前缀为 “run”（长度为 3）

题目来自力扣3598。

🔍 核心思路与步骤分解

第一步：预处理相邻字符串的公共前缀长度

首先，代码需要知道原始数组中每一对相邻字符串的最长公共前缀（LCP）长度。这是后续所有计算的基础。

• 操作：遍历整个 words 数组，从第一个元素到倒数第二个元素，依次计算 words[i] 和 words[i+1] 的LCP长度。计算工作由辅助函数 lcp(s, t string) int 完成。
• lcp函数的工作方式：该函数比较两个字符串，从第一个字符开始逐个比对，直到遇到不同的字符或其中一个字符串结束。返回匹配的字符数量。
• 结果存储：这些计算出的相邻对的LCP长度本身并不显式存储在一个数组里，但代码会在遍历过程中找出其中最大值 (mx1) 和次大值 (mx2)，并记录最大值所在的位置 i1（即第 i1 和 i1+1 个字符串组成的对拥有最长的LCP）。这一步非常关键，因为删除一个元素是否会影响到全局最大的LCP，取决于是否删除了构成这个最大LCP的那一对字符串中的某一个。

第二步：处理每个删除位置 i

接下来，代码需要模拟删除数组中每一个位置 i 的元素，并计算新数组中相邻对的最大LCP。它通过一个循环，对每个下标 i 进行如下处理：

1. 计算“跨越”删除点的LCP：

   • 情况：当删除的位置 i 不是数组的头或尾（即 0 < i < n-1）时，删除操作会使得原本不相邻的 words[i-1] 和 words[i+1] 变成新数组中的一对相邻字符串。
   • 操作：调用 lcp 函数计算 words[i-1] 和 words[i+1] 的LCP长度，记为 l。这个值代表了删除 words[i] 后新产生的一对相邻字符串的公共前缀长度。

2. 判断全局最大LCP是否受影响：

   • 核心逻辑：删除位置 i 后，原始数组中的最大LCP (mx1) 能否在新数组中保留，取决于删除操作是否破坏了构成这个最大LCP的相邻对（即位于 i1 和 i1+1 的那一对）。
   • 不受影响的情况：如果被删除的元素 i 既不等于 i1 也不等于 i1+1，那么原始的最大LCP对在新数组中依然完整存在。因此，新数组的最大LCP可能值就是 mx1 和新产生的“跨越”LCP l 之间的较大者。
   • 受影响的情况：如果被删除的元素 i 正好是 i1 或 i1+1，那么原始的最大LCP对就被破坏了。此时，新数组的最大LCP只能从原始的次大LCP (mx2) 和新产生的“跨越”LCP l 之间取较大值。

3. 存储结果：

   • 将上面判断得到的结果（max(mx1, l) 或 max(mx2, l)）存入结果数组 ans 的第 i 个位置。

第三步：输出最终结果

完成对所有下标 i 的遍历后，结果数组 ans 就已经填充完毕，其中 ans[i] 就是删除第 i 个元素后得到的新数组中所有相邻对的最大LCP长度。最后，将这个结果数组输出。

⏱️ 复杂度分析

时间复杂度：O(L)

• L 的定义：L 代表所有字符串长度的总和（题目中给出 L <= 100000）。
• 分析：
  1. 第一步预处理需要遍历所有相邻对，并对每一对进行LCP比较。最坏情况下，需要比较所有字符串的每一个字符，但字符比较的总次数不会超过所有字符串的长度总和 L。
  2. 第二步对于每个删除下标 i（共有 n 个），最多只进行一次额外的LCP计算（即计算“跨越”对的LCP）。同样，这些计算所涉及的字符比较总数也不会超过 L。
• 结论：整个算法的时间复杂度与字符串总长度 L 呈线性关系，为 O(L)。

空间复杂度：O(n)

• 分析：
  1. 算法除了输入数组外，主要额外空间用于存储结果数组 ans，其大小与输入数组长度 n 成正比。
  2. 预处理阶段只用了几个整型变量（mx1, mx2, i1）来记录关键信息。
  3. lcp 函数等操作只使用了常数级别的临时空间。
• 结论：算法的额外空间消耗主要来自于结果数组，因此空间复杂度为 O(n)。

希望这个分步解释能帮助你清晰地理解整个算法的流程和性能表现。

Go完整代码如下：

package main

import (
	"fmt"
)

func lcp(s, t string) int {
	n := min(len(s), len(t))
	for i := range n {
		if s[i] != t[i] {
			return i
		}
	}
	return n
}

func longestCommonPrefix(words []string) []int {
	n := len(words)
	mx1, mx2, i1 := -1, -1, -2
	for i := range n - 1 {
		l := lcp(words[i], words[i+1])
		if l > mx1 {
			mx2 = mx1
			mx1, i1 = l, i
		} else if l > mx2 {
			mx2 = l
		}
	}

	ans := make([]int, n)
	for i := range n {
		l := 0
		if 0 < i && i < n-1 {
			l = lcp(words[i-1], words[i+1])
		}
		if i != i1 && i != i1+1 { // 最大 LCP 没被破坏
			ans[i] = max(mx1, l)
		} else {
			ans[i] = max(mx2, l)
		}
	}
	return ans
}

func main() {
	words := []string{"jump", "run", "run", "jump", "run"}
	result := longestCommonPrefix(words)
	fmt.Println(result)
}

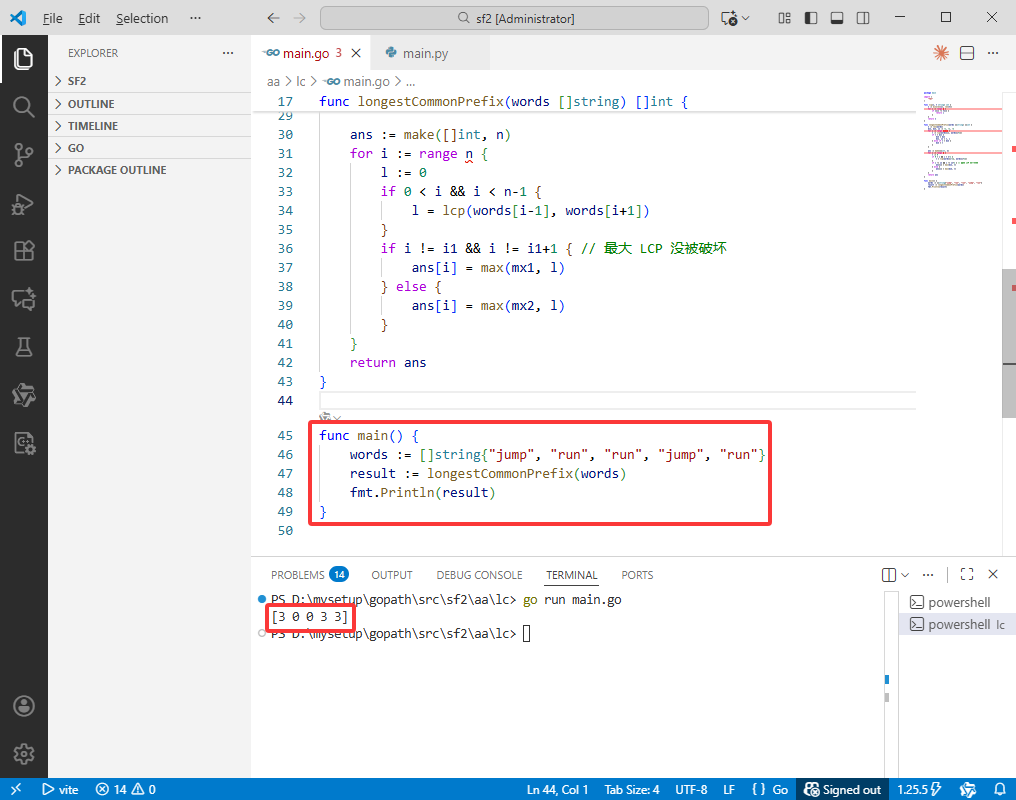
Python完整代码如下：

# -*-coding:utf-8-*-

from typing import List

def lcp(s: str, t: str) -> int:
    """返回两个字符串的最长公共前缀长度"""
    n = min(len(s), len(t))
    for i in range(n):
        if s[i] != t[i]:
            return i
    return n

def longestCommonPrefix(words: List[str]) -> List[int]:
    n = len(words)
    mx1, mx2, i1 = -1, -1, -2
    
    # 找出相邻单词间的最大和次大LCP
    for i in range(n - 1):
        l = lcp(words[i], words[i + 1])
        if l > mx1:
            mx2 = mx1
            mx1, i1 = l, i
        elif l > mx2:
            mx2 = l
    
    ans = [0] * n
    for i in range(n):
        # 计算删除当前单词后的可能LCP
        l = 0
        if 0 < i < n - 1:
            l = lcp(words[i - 1], words[i + 1])
        
        # 如果当前索引不在最大LCP对应的相邻索引中，则最大LCP仍可用
        if i != i1 and i != i1 + 1:
            ans[i] = max(mx1, l)
        else:
            ans[i] = max(mx2, l)
    
    return ans

if __name__ == "__main__":
    words = ["jump", "run", "run", "jump", "run"]
    result = longestCommonPrefix(words)
    print(result)  # 输出: [0, 3, 3, 0, 3]

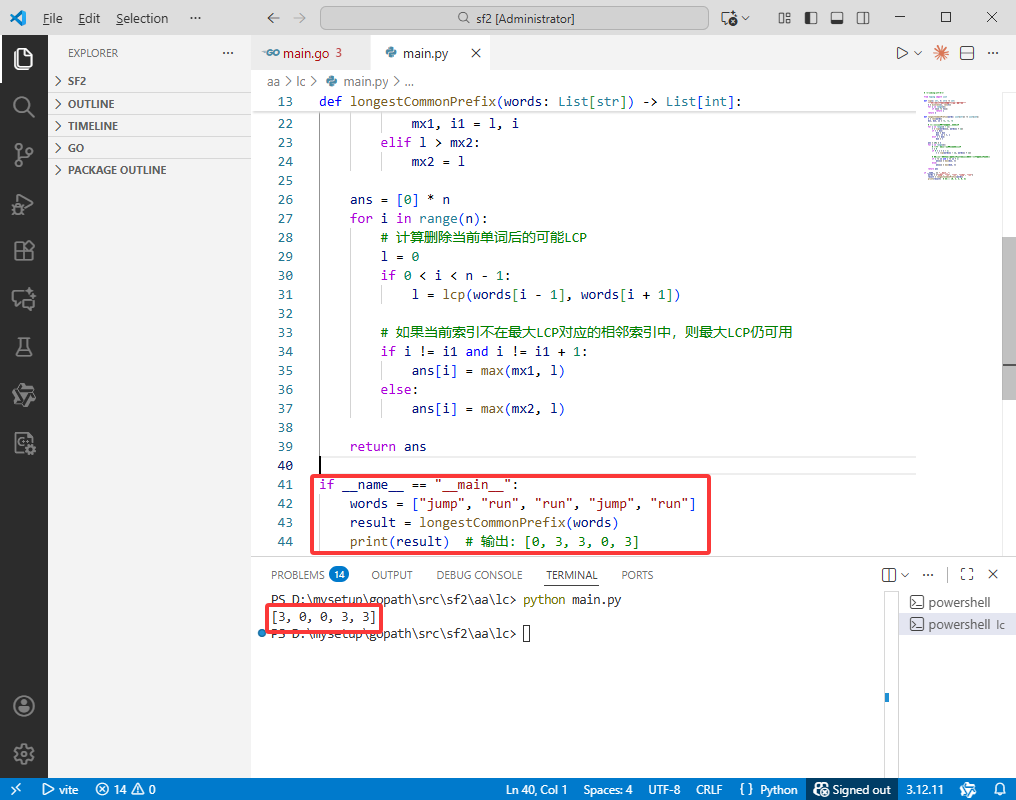
C++完整代码如下：

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>

using namespace std;

int lcp(const string& s, const string& t) {
    int n = min(s.length(), t.length());
    for (int i = 0; i < n; i++) {
        if (s[i] != t[i]) {
            return i;
        }
    }
    return n;
}

vector<int> longestCommonPrefix(const vector<string>& words) {
    int n = words.size();
    int mx1 = -1, mx2 = -1, i1 = -2;

    // 找出相邻单词间的最大和次大LCP
    for (int i = 0; i < n - 1; i++) {
        int l = lcp(words[i], words[i + 1]);
        if (l > mx1) {
            mx2 = mx1;
            mx1 = l;
            i1 = i;
        } else if (l > mx2) {
            mx2 = l;
        }
    }

    vector<int> ans(n, 0);
    for (int i = 0; i < n; i++) {
        int l = 0;
        if (0 < i && i < n - 1) {
            l = lcp(words[i - 1], words[i + 1]);
        }

        if (i != i1 && i != i1 + 1) {
            ans[i] = max(mx1, l);
        } else {
            ans[i] = max(mx2, l);
        }
    }

    return ans;
}

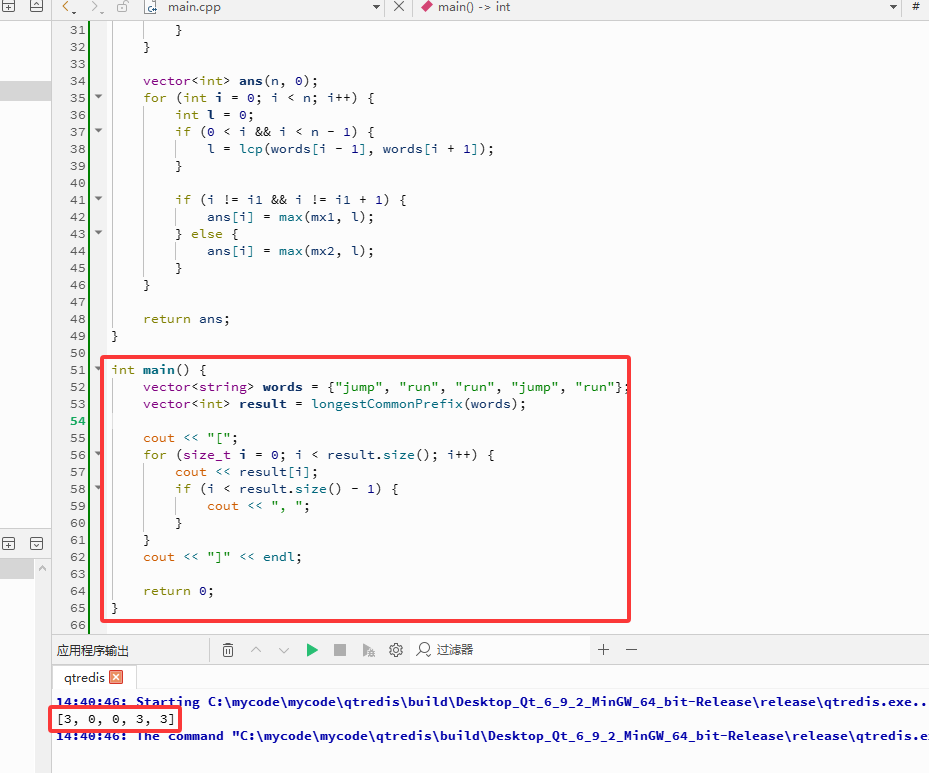
int main() {
    vector<string> words = {"jump", "run", "run", "jump", "run"};
    vector<int> result = longestCommonPrefix(words);

    cout << "[";
    for (size_t i = 0; i < result.size(); i++) {
        cout << result[i];
        if (i < result.size() - 1) {
            cout << ", ";
        }
    }
    cout << "]" << endl;

    return 0;
}