KDD 2022| 使用约束能量模型的抗体CDR 设计
这次为大家分享的是来自伊利诺伊大学厄巴纳-香槟分校的Jimeng Sun教授团队发表在KDD一篇上名为《Antibody Complementarity Determining Regions (CDRs) design using Constrained Energy Model》的文章。近年来涌现出许多计算设计抗体CDR环的工作,但面临着CDR 环维持特定几何形状的挑战。在这篇文章中,作者设计了一个约束流形来表征 CDR 环的几何约束,接着设计了约束流形中的能量模型Constrained Energy Model (CEM)。

1.介绍
抗体药物的主要优势在于对抗原的高度特异性,副作用较少,治疗性抗体已成为近年来开发的用于治疗各种人类疾病的主要一类新药。抗体工程就设计方法而言,抗体的大部分亲和力和特异性受到抗体可变域上称为互补决定区 (CDR) 的一组结合环的调节。对抗体设计,尤其是 CDR 环设计的计算机方法的开发有很高的需求。然而,当前的抗体发现和开发程序严重依赖于高通量筛选和实验启发式的混合,成本较大。
最近已有许多机器学习的方法来设计新的抗体,这些方法中的大多数将抗体设计问题表述为氨基酸序列设计或 3D 图设计任务。然而仍然存在几个挑战:(1)现有的抗体设计方法大多没有考虑抗体 CDR 环具有特定的几何形状,这可能导致产生无效的CDR环。(2) 大多数现有的深度生成模型没有利用外部知识,纯粹从数据中学习,阻碍了它们整合约束的能力。
作者据此做出了如下贡献:(1) 将抗体 CDR 设计制定为受约束的 3D 生成任务,并定义一个受约束的流形来表示所有几何有效 CDR 循环。(2) 设计了一个约束能量模型,该模型在定义的流形上学习 3D 结构。理论分析表明,在流形上进行约束学习所需的样本量约为无约束学习所需样本量的三分之二,实验结果证实了所提出方法的有效性,该方法在3D均方误差(RMSD)方面相对降低了 33.4%,在氨基酸序列困惑度(perplexity)方面相对提高8.4%。
2.方法
CDR环有效性和流形M的定义
抗体是一种特殊的蛋白质,呈对称和 Y 形。在 Y 型抗体中,有 6 个 CDR 环,轻链上有 L1、L2、L3 环,重链上有 H1、H2、H3 环。如图 1 所示,对称单元的每一半都有两条链:一条重链 (H) 和一条轻链 (L)。抗体的大部分亲和力和特异性由一组结合环调节,称为互补决定区 (CDR),这些环位于两条链中每条链的可变结构域上。与 L1、L2、L3 环相比,抗体 CDR 中的 H1、H2、H3 环在其与潜在抗原的结合能力中起着至关重要的作用。因此,本文将注意力集中在分别设计 H1、H2 和 H3 环上。
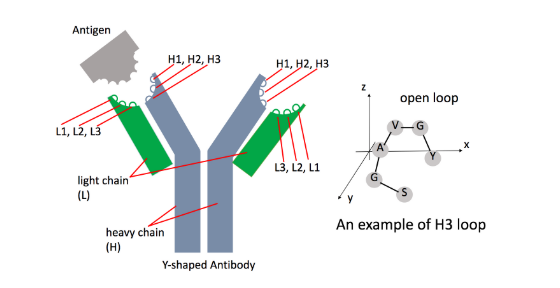
图 1 数据表示。抗体是一种特殊的蛋白质,具有对称的 Y 形,对称单元的每一半都有两条链:一条重链 (H) 和一条轻链 (L)。总共有四个链,两个相同的 H/L 链。大部分的结合亲和力(对特定抗原)由一组称为互补决定区 (CDR) 的结合环调节,这些环位于 H 和 L 链中的每一个的可变结构域上。
基于经验和知识,作者定义了CDR环的有效性,具体来说,定义生成的 3D CDR环在满足以下两个约束时具有有效性:
-
肽键长度。
多个氨基酸通过肽键连接在一起,形成一条单链。
肽键的长度是相对固定的,即连接的氨基酸之间的距离是一个常数。
-
开环。
CDR 的形状是一个开环,如图 1 所示,其中第一个和最后一个氨基酸之间的距离在特定范围内。
接下来作者定义了流形M的形式,如下图公式所述,具体推导流程可以自行查阅原文。
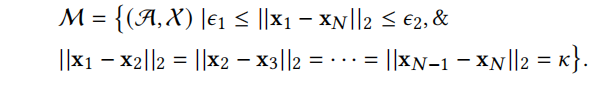
能量功能的神经结构
作者提出参数化能量函数E,如E通常是一个输出为标量的神经网络。由于能量度量是一个标量,并且对于数据点是可微的,因此能量模型可以反向传播梯度来直接更新数据点。在三维图的背景下,我们选择一个平移的、旋转不变的图神经网络作为参数化的能量函数来表示数据(三维图)。因此为了表示 3D CDR 环,作者利用最先进的等变图神经网络 (EGNN),以便 3D 图(坐标)上的平移和旋转不会改变 EGNN 的输出。
为了学习具有最大似然学习的能量模型,作者将最大化对数似然学习关于真实数据的分布,即一个理想的能量函数将较低的能量分配给真实数据,而将较高的能量分配给其他数据点。然而,最大似然学习只会鼓励对真实数据的能量较低,而且是不够的。为了解决这个问题,采用了对比差异来创建幻想样本,更具体地说,幻想样本来自于基于能量的概率分布P。为了从P中采样,作者经过尝试,最终采用基于梯度的马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)。
无约束能量模型和约束能量模型(CEM)
图2介绍了无约束能量模型和约束能量模型的区别,在原文中作者详细推导了两个能量模型的计算公式,并阐述它们之间的区别。
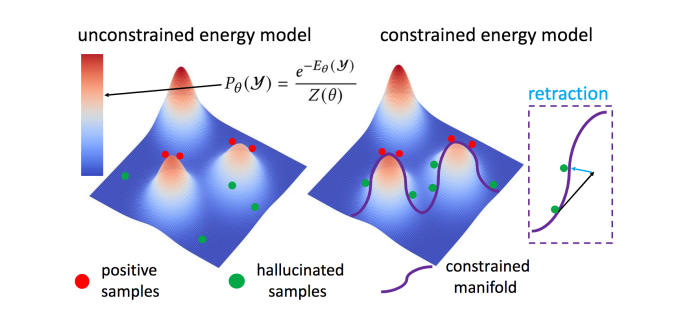 图 2 约束能量模型和无约束能量模型的区别。
图 2 约束能量模型和无约束能量模型的区别。
与无约束能量模型不同,约束能量模型在约束流形 M中的所有 CDR 循环上定义了参数化概率分布 P,M 是包含所有几何有效 CDR 环的约束流形,E是一个能量函数,通常是一个输出为标量的神经网络。理想情况下,具有较低能量的数据 Y 对应于较高的概率/可能性 P。归一化常数Z是约束流形 M 上的积分,并且在计算上仍然难以处理。
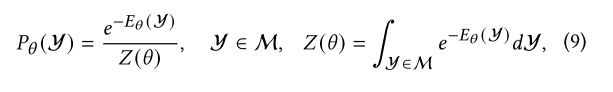
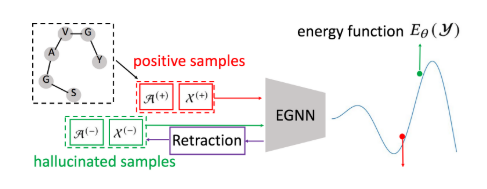
图 3 CEM 管道。正样本和幻想样本都限于受约束的流形 M。在学习过程中,CEM 交替采取以下两个步骤:(i)通过最大化等式中的学习目标来更新约束能量模型,其中正样本(红色)的能量函数被下推,幻想样本(绿色)的能量函数被推高;(ii) 通过从P中采样来更新幻想样本,并按照公式进行缩回(紫色框)。回缩是将 CDR 回路投影到受约束的流形上。然后在推理过程中,修复约束能量模型并从P中抽取样本。
样本复杂度分析
在原文3.4节中,作者用数学理论分析了使用CEM相比无约束模型训练,只需要约2/3的样本。即在有约束流形M上的学习比无约束方法需要更少的样本复杂度。有兴趣的朋友可以下载原文观看。
3.实验
作者采用的是结构抗体数据库 SabDab2 ,一个包含蛋白质数据库 (PDB) 中可用的 5,494 种抗体的数据库。一种抗体可能包含多个 CDR 环(氨基酸序列和 3D 结构)。在过滤 CDR 结构不可用的抗体后,获得了 8,381 个 CDR 环。H1、H2 和 H3 的平均长度和标准偏差分别为 7.2 ± 0.6、5.9 ± 0.7 和 12.3 ± 4.4。数据点以 8:1:1 的比例随机分为训练集、验证集和测试集。数据采用 PDB 文件格式,所有原子坐标均可用。用𝛼-碳原子的坐标来表示氨基酸的坐标。
作者从序列和结构两个方面评价了生成的CDR环:
氨基酸序列水平指标包括:

4.结果
对于所有比较的方法,作者在 H1、H2、H3 循环上执行生成任务,并在表中报告。结果对于每个任务和每种方法,作者使用不同的随机种子和数据拆分进行了 5 次独立运行。表1显示了所有指标的平均结果及其标准偏差。作者还进行了 t 检验来比较 CEM 和最佳基线方法 (IR-GNN) 之间的差异。
从表1中,有以下观察结果:(1)作者的方法在PPL,RMSD和 %V方面显着优于所有基线方法。(2) H1 与H2 与H3的挑战性:在所有三种设计任务中,包括H1、H2、H3循环,几乎所有方法在H3生成任务中获得最高的PPL、RMSD和较低的有效性。这与现有的知识一致,即 CDR H3 循环具有最高的可变性和最具挑战性的设计。(3) 多样性:EBM、CEM、IR-GNN 和 AR-GNN 在多样性方面表现相似,验证了本文的方法可以彻底探索氨基酸序列空间。
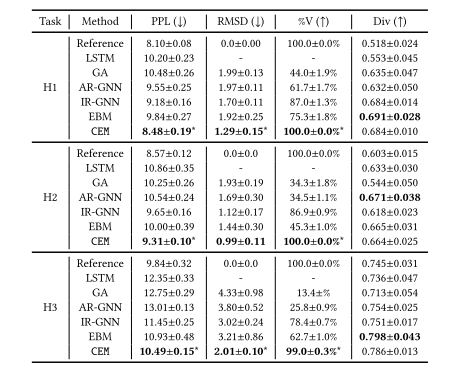
表 1 SabDab2上的从头抗体 CDR 环(包括 H1、H2、H3)设计结果。对于每个任务和每个方法,使用不同的随机种子和数据拆分进行 5 次独立运行。报告指标的平均值和标准偏差。
CEM性能优于普通能量模型的原因在于,CEM 将学习空间限制在受约束的流形 M 上,并且只需要区分(即分配更低或更高的能量值)流形上的数据点。如图4所示,作者用 CDR H3 环路设计中的两个示例分析CEM的结果。
对于每个示例,展示了 CEM和参考(测试集中的实际 CDR 环路)和 IR-GNN(最佳基线方法)的 CDR 环路的 3D 结构) 作为比较。对于每个图像,本文方法和 IR-GNN 的构象(3D 结构)通过对齐函数进行旋转和平移,以便根据 RMSD 度量,它们与参考构象的距离最小。作者发现在氨基酸序列水平上,其方法比 IR-GNN 更类似于参考构象,例如,在第一个示例(左)中,“EDGYFFT”(由 CEM 生成)之间的相似性和“DDGYFDT”(参考)为0.71,而“DFDWFAT”(IR-GNN)和“DDGYFDT”(参考)之间的相似度仅为0.43。此外,与 IR-GNN 相比,CEM 的困惑度更低(越低越好),并且在两个示例中都更接近参考构象(更低的 RMSD 分数)(0.86 对 1.71 和 0.50 对 0.93)。这些示例提供了 CEM 的直观演示。
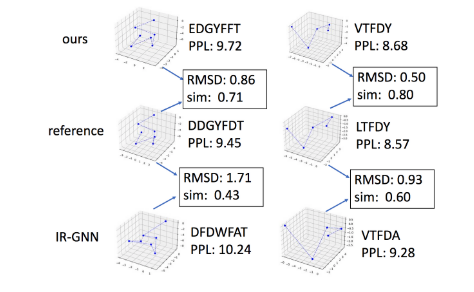 图4 关于 CDR H3 环路设计的两个示例。
图4 关于 CDR H3 环路设计的两个示例。
5.结论
作者提出了用于设计 3D 抗体 CDR 环的约束能量模型 (CEM)。首先为所有满足几何约束的 CDR 环设计一个约束流形。然后设计了约束能量模型,该模型从约束流形中的正样本和幻想样本中学习,并更新约束流形中的幻想样本。理论分析表明,在流形上进行约束学习所需的样本量小于无约束学习样本量的三分之二左右。全面的实证研究验证了 CEM 在设计 CDR H1、H2、H3 回路方面的优势。
参考资料
Fu, Tianfan, and Jimeng Sun. "Antibody Complementarity Determining Regions (CDRs) design using Constrained Energy Model." Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. 2022.
代码
https://github.com/futianfan/energy_model4antibody_design.
文章来源: drugai.blog.csdn.net,作者:DrugAI,版权归原作者所有,如需转载,请联系作者。
原文链接:drugai.blog.csdn.net/article/details/126737000
- 点赞
- 收藏
- 关注作者


评论(0)