数据结构与算法之让我们种下一棵字典树(Java/C++双语言实现)

举报
未见花闻 发表于 2022/11/30 21:31:38 2022/11/30
【摘要】 ⭐️前面的话⭐️本篇文章将介绍一种经常使用的数据结构——字典树，它又称Tire树，前缀树，字典树，顾名思义，是关于“字典”的一棵树。这个词典中的每个“单词”就是从根节点出发一直到某一个目标节点的路径，路径中每条边的字母连起来就是一个单词，今天我们就来种下这样的一棵树，它在竞赛和面试笔试都会经常用到。 1.字典树概述 1.1什么是字典树字典树，又被称为Tire树，或者称为前缀树，常常用于算法竞...

⭐️前面的话⭐️

本篇文章将介绍一种经常使用的数据结构——字典树，它又称Tire树，前缀树，字典树，顾名思义，是关于“字典”的一棵树。这个词典中的每个“单词”就是从根节点出发一直到某一个目标节点的路径，路径中每条边的字母连起来就是一个单词，今天我们就来种下这样的一棵树，它在竞赛和面试笔试都会经常用到。

封面区

1.字典树概述

1.1什么是字典树

字典树，又被称为Tire树，或者称为前缀树，常常用于算法竞赛当中，当然面试笔试当中也是可能遇到的。

字典树，顾名思义，是关于“字典”的一棵树。即：它是对于字典的一种存储方式（所以是一种数据结构而不是算法）。这个词典中的每个“单词”就是从根节点出发一直到某一个目标节点的路径，路径中每条边的字母连起来就是一个单词。

字典树可以用来储存字符串中的每个字母，并且能够快速第查询出来，比如有下面一组单词：

aadb
abcd
bcgff
begin
abc

将上述字符，以树形方式存储，结构如下，这种结构就是一种字典树：
字典树
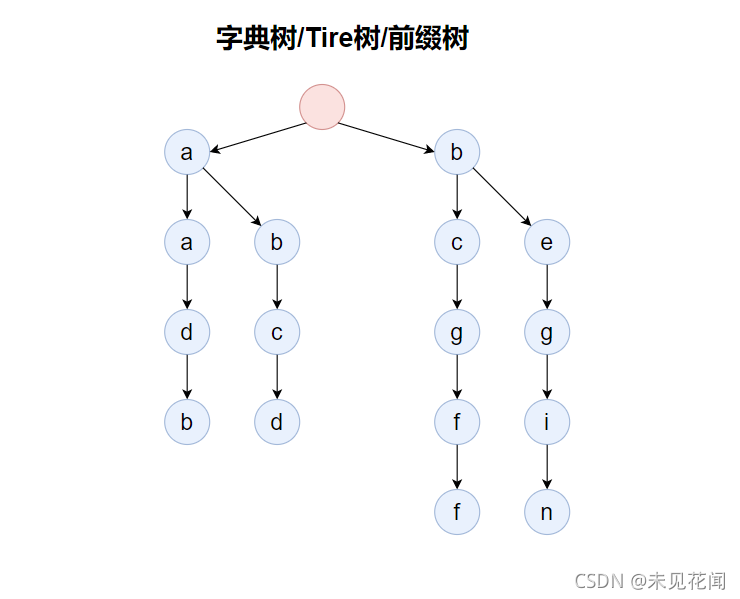
为了表示存储在字典树中最后一个单词是什么，一般还会有一组配套的标记end，表示当前字母是否是某一个单词的结尾，上面那一棵前缀树根本不知道存的时候有哪些单词存进去了，可能字母a也存在，可能单词ab也存在等等，所以我们需要一个结尾标记来标记单词结尾的位置，于是得到了一下的字典树。

带上标记
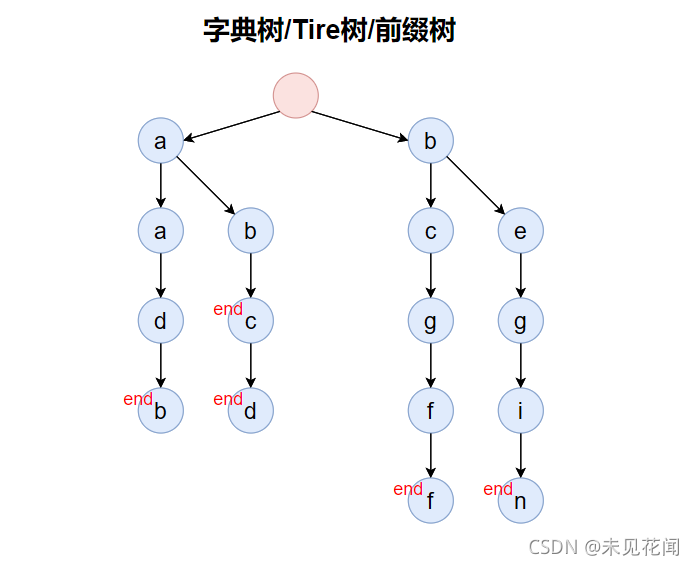
知道了什么是字典树，那字典树又有什么作用呢？下面来说明一下字典树常出现的情况。

1.2字典树的功能

根据字典树的概念，我们可以发现：字典树的本质是把很多字符串拆成单个字符的形式，以树的方式存储起来。所以我们说字典树维护的是”字典“。那么根据这个最基本的性质，我们可以由此延伸出字典树的很多妙用。简单总结起来大体如下：

1、维护字符串集合（即字典）。

2、向字符串集合中插入字符串（即建树）。

3、查询字符串集合中是否有某个字符串（即查询）。

4、统计字符串在集合中出现的个数（即统计）。

5、将字符串集合按字典序排序（即字典序排序）。

6、求集合内两个字符串的LCP（Longest Common Prefix，最长公共前缀）（即求最长公共前缀）。

我们可以发现，以上列举出的功能都是建立在“字符串集合”的基础上的。再一次强调，字典树是“字典”的树，一切功能都是“字典”的功能。这也为我们使用字典树的时候提供了一个准则：看到一大堆字符串同时出现，就往哈希和Trie树那边想一下。

2.字典树的实现思路

2.1字典树的创建与插入功能

字典树的插入本质上就是通过将字符串的每个字符都存入这个“字典”上，最终所形成的一棵树，为了表示方便，以下图中的红色结点表示字典树的根结点，蓝色结点表示字典树的普通字符，绿色结点表示字典树的结束字符，也就是原某一字符串的最后一个字符。

构建字典树的过程如下，字典树的根结点一般为空，首先插入单词aadb：

1

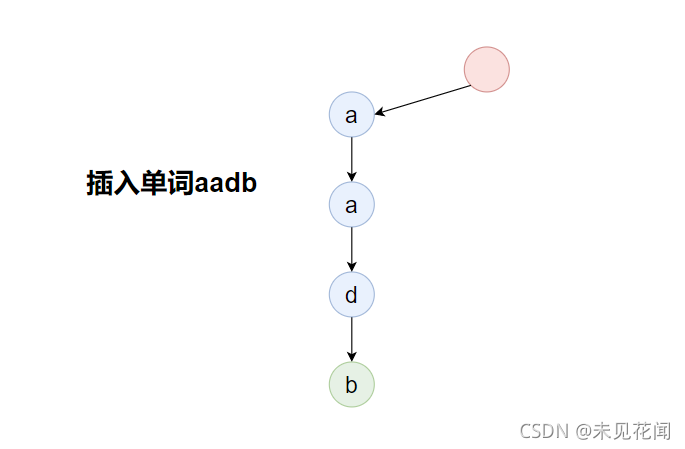
插入单词abcd:
2

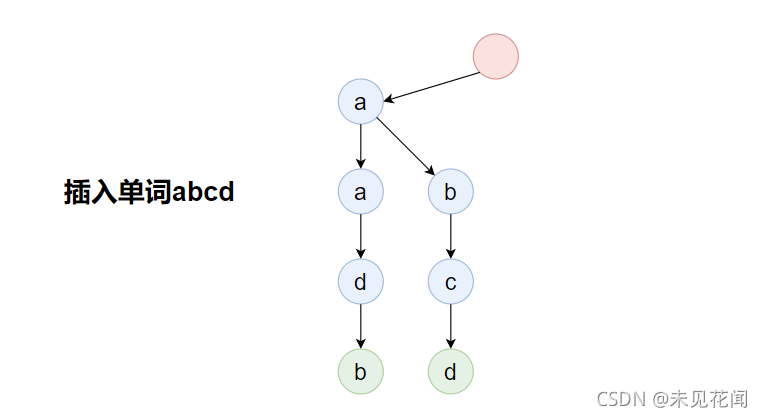
插入单词bcgff：

3

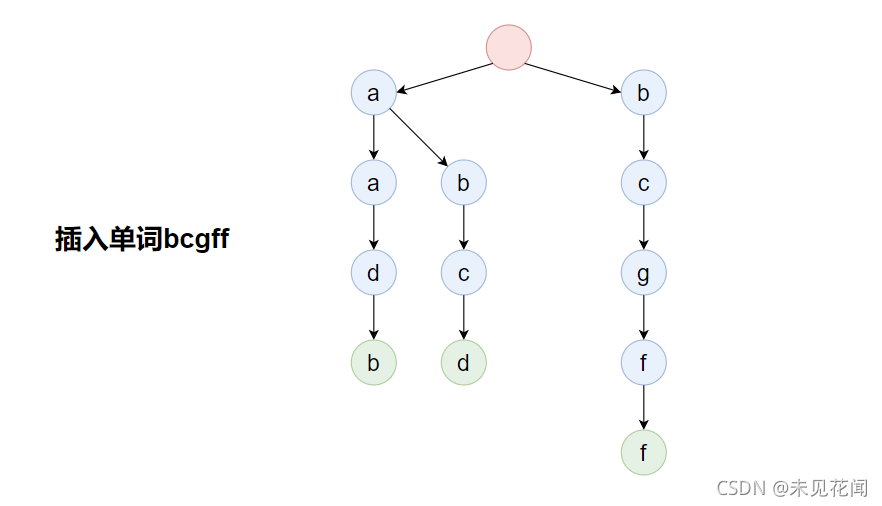
插入单词begin：

4

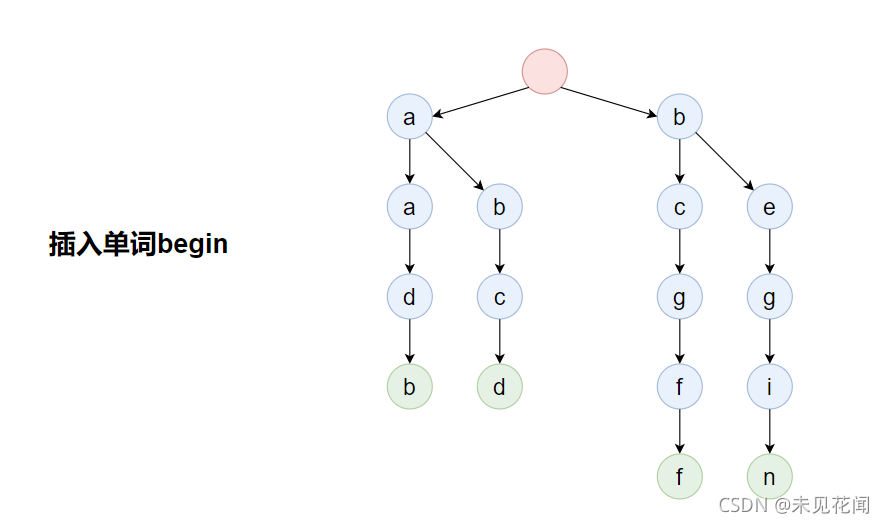
插入单词abc：
5
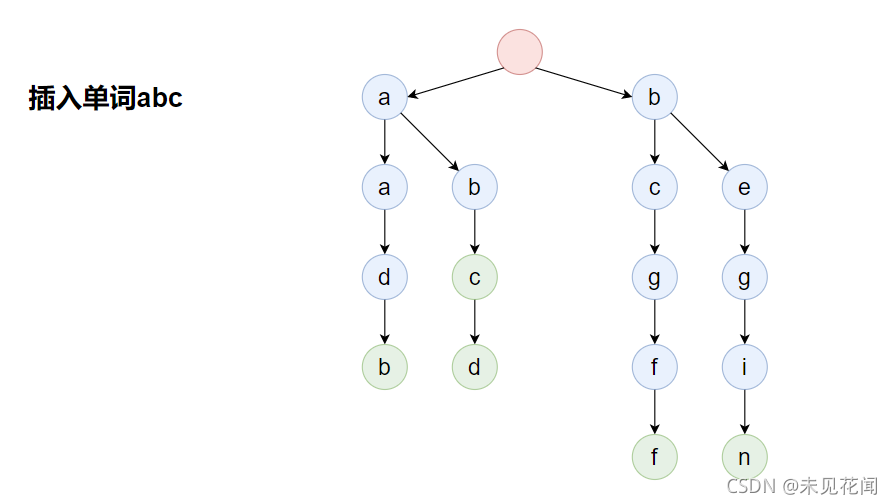
上面我们从思想层面，描述了字符串插入字符到字典树的过程，下面我们来解释如何使用代码实现上述的思路。

首先我们创建一个结点类，就叫做TireNode类吧，next数组表示子结点在哪里，end用来标记是否是一个字符串的结尾字符，翻译成代码就是下面的这一段：
Java版本：

//实现class版本的前缀树
class TireNode {
    public boolean end;    //表示是否是结束字符
    public TireNode[] next = new TireNode[26];  //表示某个字符的下一个结点的位置
    
    //空构造方法
    public TireNode(){}
}

C++版本：

class TireNode
{
public:
    // 记录该字符是不是最后一个字符
    bool end;
    // 记录子结点
    TireNode* next[26] = {nullptr};
    TireNode () {}
};

其中next数组中申请了26个结点，创建这么多结点的意思是按照下标号来映射某一字母，如0号下标映射字母a，1号下标映射字母b，以此类推，这些结点的意义是表示某字符串中一个字母的下一个字母的位置。

然后我们创建一个Tire类表示字典树类，我们需要一个根结点，就叫做tire吧，也就是图中红色的结点，该结点只是用来指向每个字符串第一个字母的位置，因此它本身并不表示任何字符，有一个插入字符的方法，还有几个查询的方法。

//实现过程中用到的全局变量 需要放到某一个类中，博主实现代码放在Main类中
class Main {
    //最大字符串个数
    private static final int N = (int) 1e5 + 2333;
    //根结点
    private static TireNode tire = new TireNode();
    // 计数器 记录当前的编号
    private static int idx = 0;
    //层数记录器
    private static int[] cnt = new int[N]; 
    //其他...
}
class Tire {
	//根结点
	public TireNode tire = new TireNode();
	//插入操作
	public void insert() {}
	//查询操作
	//返回字符串是否在字典树内
	public boolean query(char[] cs) {}
	//如果在字典树中查询到一个字符串返回它出现的次数，反之如果没有找到返回0
	public int hashQuery(char[] cs) {}
	//查询某字符串是否是字典树某一个字符的子串
	public boolean subQuery(char[] cs) {}
}

C++版本：

//实现过程中用到的全局变量
#include <iostream>
using namespace std;

const int N = (int) 1e5 + 2333;
// 记录每个以特定id对应字符结尾字符串的个数
int cnt[N];
// 记录插入字符到字典树的实时id
int idx;
// 记录操作的字符串
char str[N];
class Tire 
{
public:
	TireNode* tire = new TireNode();
	void insert() {}
	boolean query(char* cs) {}
	int hashQuery(char* cs) {}
	boolean subQuery(char* cs) {}
}

插入操作的思路就是，遍历传入字符串中的每一个字符，并同步遍历字典树结点cur，从根节点开始，找到该字符映射在next数组的位置u，如果发现对应位置为空，表示这个字符还没有被插入到字典树，我们就新建一个结点，并赋值给next[u]，赋值完成后，并将cur更新为该新结点next[u]，直到字符串遍历完成为止，遍历完后，我们将最后一个字符对应的TireNode对象的end标记为true，表示该字符是结尾字符，实现代码如下：

Java版本：

//插入操作
    private static void insert(char[] cs) {
        TireNode cur = tire;
        int p = 0;
        for (int i = 0; i < cs.length; i++) {
            int u = cs[i] - 'a';
            if (cur.next[u] == null) cur.next[u] = new TireNode();
            
            cur = cur.next[u];
        }
        
        //将最后一个字符做上end标记
        cur.end = true;
    }

C++版本：

    //插入操作
    void insert(char* cs)
    {
        TireNode* cur = tire;
        for (int i = 0; cs[i] != '\0'; i++)
        {
            int u = cs[i] - 'a';
            //cout << u << endl;
            if (cur->next[u] == nullptr) cur->next[u] = new TireNode();
            cur = cur->next[u];
        }
        
        cur->end = true;
    }

2.2字典树的查询功能

2.3.1基本的查询功能

字典树查询操作其实和插入操作大同小异，遍历的方式与插入一模一样，只不过如果遇到某字符对应的next数组元素为空，表示该字典树不包含该字符串，直接返回false，就是相当于字典树里面存了ab，查询字符串为abc，字符串遍历到c时，对应位置next数组元素为空。

遍历完所有查询字符串，所有字符都能在next数组中匹配上，此时能说明一定含有该字符吗？对于这个问题，我们来举一个栗子，字典树里面存了字符串abc，查询字符串为ab，很明显可以顺利遍历完查询字符串，但是字符串ab并不在字典树当中，所以说就算所有的字符与next数组匹配，但是并一定就在字典树内，此时end标记的作用就出来了，我们只需判断查询字符串的最后一个字符是否是字典树中某一个字符串的最后一个字符就可以了，就比如上面的例子，查询字符串的最后一个字符b，在字典树当中并不是最后一个字符，所以返回false，如果是最后一个字符，那就返回true，根据这个思路我们可以写出代码：

Java代码实现：

    //查询操作 返回是否存在
    private static boolean query(char[] cs) {
        TireNode cur = tire;
        for (int i = 0; i < cs.length; i++) {
            int u = cs[i] - 'a';
            if (cur.next[u] == null) return false;
            
            cur = cur.next[u];
        }
        
        return cur.end;
    }

C++代码实现：

    //查询操作
    bool query(char* cs)
    {
        TireNode* cur = tire;
        for (int i = 0; cs[i] != '\0'; i++)
        {
            int u = cs[i] - 'a';
            
            if (cur->next[u] == nullptr) return false;
            
            cur = cur->next[u];
        }
        
        if (!cur->end) return false;
        
        return true;
    }

2.3.2查询某个字符串是否为字典树中某一字符串的子串

查询一个字符串是否是另外一个字符串的子串，与普通匹配查询是一样的，只不过最后不需要进行end标记的判断，因为要查询字符串中的字符位置都在字典树中一一匹配，那么该查询字符串那肯定就是字典树中某一个字符串的子串了，实现代码：

Java版本代码：

    //查询操作 返回是否存在子串
    private static boolean query(char[] cs) {
        TireNode cur = tire;
        for (int i = 0; i < cs.length; i++) {
            int u = cs[i] - 'a';
            if (cur.next[u] == null) return false;
            
            cur = cur.next[u];
        }
        
        return true;
    }

C++版本代码：

    //查询操作
    bool subQuery(char* cs)
    {
        TireNode* cur = tire;
        for (int i = 0; cs[i] != '\0'; i++)
        {
            int u = cs[i] - 'a';
            
            if (cur->next[u] == nullptr) return false;
            
            cur = cur->next[u];
        }
        
        return true;
    }

2.3.3统计字典树中每个字符串的个数

对于这个问题，其实思路有很多种，你可以搭配一个哈希表来对字符串个数进行计数，也可以通过对字典树中的每一个字符进行编号，首先我们需要知道，在字典树中作为结尾字符的结点对应的字符串是唯一的，因为字符串插入到字典树后，从根节点到字符串最后一个字符对应字符的路径是唯一的也是确认的，如果另外一个字符串路径与该字符串相同，那么另外一个字符串的结尾字符落在的字典树的位置一定与原字符相同，对于该字符串的子串或者作为另外一个字符串的子串，其在字典树上的路径会出现重合，但是结尾字符所对应字典树的位置一定是不相同的。

比如字符串abc与abcd，虽然前面三个字符位置是一模一样的，但是结束位置是不相同的，如果相同，那一定就是相同的字符串。
4
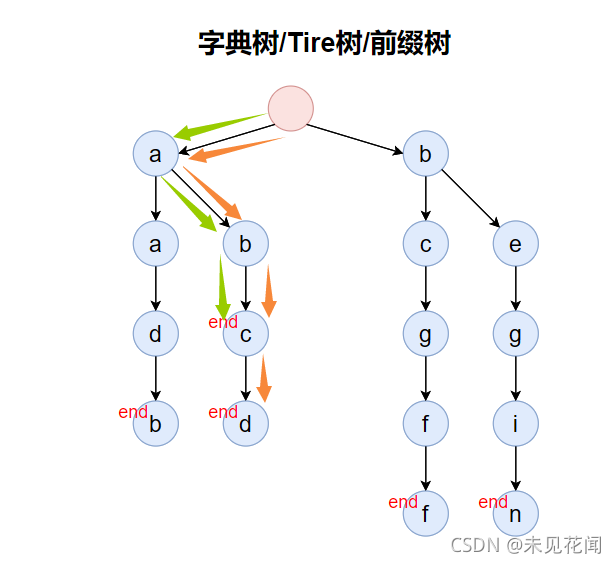
根据这个性质，我们可以在插入的时候，将所有的字符都标上一个唯一的编号，然后我们以结束位置结点的编号为基准，创建一个数组，将编号映射到数组下标并进行计数，毕竟一个字符串对应结束位置是唯一的，那么自然编号也是唯一的，那么就可以间接地通过编号来代表字符串进行计数。

因为计数是在字典树创建或插入的时候完成的，所以查询的时候我们可以通过所给字符串找到字符串的结尾位置的编号，来获取对应字符串在字典树中出现的次数。
5

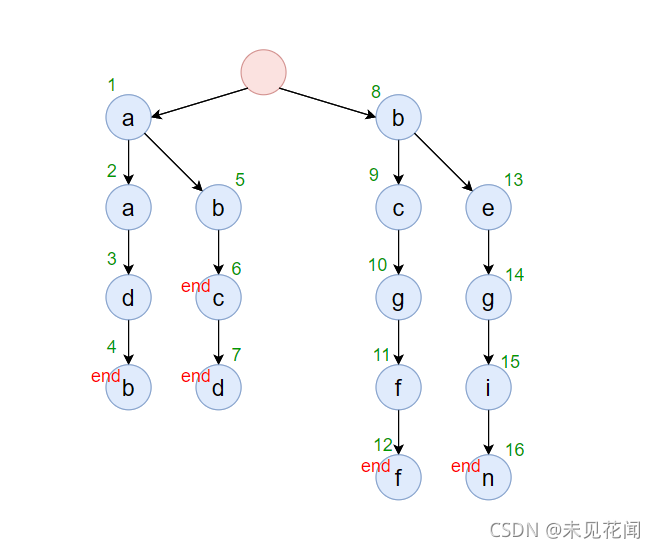
为了编号方便，我们可以在节点类中加上一个属性id，表示当前结点的编号：

Java:

class TireNode {
    public boolean end;    //表示是否是结束字符
    public TireNode[] next = new TireNode[26];  //表示某个字符的下一个结点的位置
    public int id;              //表示该字符在字典树中的编号
    
    //空构造方法
    public TireNode(){}
    
    //初始化id构造
    public TireNode (int id) {
        this.id = id;
    }
}

C++:

class TireNode
{
public:
    // 记录该字符是不是最后一个字符
    bool end;
    // 记录子结点
    TireNode* next[26] = {nullptr};
    // 记录以该字符结尾的id
    int id;
    
    TireNode () {}
    
    TireNode(int _id) {
        id = _id;
    }
};

将计数操作嵌入到插入操作的实现代码如下：
Java实现代码：

//其中idx为全局变量，作用是递增生成编号，为插入时的每一个节点编号
    //插入操作
    private static void insert(char[] cs) {
        TireNode cur = tire;
        int p = 0;
        for (int i = 0; i < cs.length; i++) {
            int u = cs[i] - 'a';
            if (cur.next[u] == null) cur.next[u] = new TireNode(++idx);
            
            cur = cur.next[u];
        }
        
        //将最后一个字符做上end标记
        cur.end = true;
        // 对以该字符结尾的字符串进行计数
        cnt[cur.id]++;
    }

C++实现代码：

//其中idx为全局变量，作用是递增生成编号，为插入时的每一个节点编号
//cpp实现过程中，将字符串输入到了一个足够大的char数组当中，所以可以使用判断\0来判断结尾
//cpp使用string就可以做到与java一模一样了
    //插入操作
    void insert(char* cs)
    {
        TireNode* cur = tire;
        for (int i = 0; cs[i] != '\0'; i++)
        {
            int u = cs[i] - 'a';
            //cout << u << endl;
            if (cur->next[u] == nullptr) cur->next[u] = new TireNode(++idx);
            cur = cur->next[u];
        }
        
        cur->end = true;
        //计数
        cnt[cur->id]++;
    }

查询操作也是一样的，只不过把返回值改为结尾位置编号对应的计数数组中的计数次数，实现代码：

Java版本：

    // 查询操作 返回查询到字符串当前的个数
    private static int hashQuery(char[] cs) {
        TireNode cur = tire;
        for (int i = 0; i < cs.length; i++) {
            int u = cs[i] - 'a';
            if (cur.next[u] == null) return 0;
            
            cur = cur.next[u];
        }
        
        if (cur.end) return cnt[cur.id];
        
        return 0;
    }

C++版本：

    //查询操作
    int hashQuery(char* cs)
    {
        TireNode* cur = tire;
        for (int i = 0; cs[i] != '\0'; i++)
        {
            int u = cs[i] - 'a';
            
            if (cur->next[u] == nullptr) return 0;
            
            cur = cur->next[u];
        }
        
        if (!cur->end) return 0;
        
        return cnt[cur->id];
    }

3.实战演练：Trie字符串统计

3.1题目链接

835. Trie字符串统计

3.2题目详情

维护一个字符串集合，支持两种操作：

I x 向集合中插入一个字符串 x；
Q x 询问一个字符串在集合中出现了多少次。
共有 N 个操作，所有输入的字符串总长度不超过 1 0 5 10^5 ，字符串仅包含小写英文字母。

输入格式
第一行包含整数 N，表示操作数。

接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式
对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。

每个结果占一行。

数据范围
1 ≤ N ≤ 2 ∗ 1 0 4 1≤N≤2∗10^4

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

3.3解题思路

其实就是对我们上面所讲的字典树各个操作的综合题而已，思路就不多提了，不过在竞赛当中，用的更多的是使用数组实现字典树，仅仅就是将class实现的方式改为使用纯数组实现罢了，思路是一模一样的，我就不具体细说数组版本实现的细节了，后面会给出该题数组版本的实现代码。

3.4实现代码（C++/Java讲解实现版本）

Java代码实现：

import java.util.*;
//实现class版本的前缀树
class TireNode {
    public boolean end;    //表示是否是结束字符
    public TireNode[] next = new TireNode[26];  //表示某个字符的下一个结点的位置
    public int id;              //表示该字符在字典树中的编号
    
    //空构造方法
    public TireNode(){}
    
    //初始化id构造
    public TireNode (int id) {
        this.id = id;
    }
}

class Main {
    //最大字符串个数
    private static final int N = (int) 1e5 + 2333;
    //根结点
    private static TireNode tire = new TireNode();
    // 计数器 记录当前的编号
    private static int idx = 0;
    //层数记录器
    private static int[] cnt = new int[N]; 
    
    
    //插入操作
    private static void insert(char[] cs) {
        TireNode cur = tire;
        int p = 0;
        for (int i = 0; i < cs.length; i++) {
            int u = cs[i] - 'a';
            if (cur.next[u] == null) cur.next[u] = new TireNode(++idx);
            
            cur = cur.next[u];
        }
        
        //将最后一个字符做上end标记
        cur.end = true;
        // 对以该字符结尾的字符串进行计数
        cnt[cur.id]++;
    }
    
    // 查询操作 返回查询到字符串当前的个数
    private static int hashQuery(char[] cs) {
        TireNode cur = tire;
        for (int i = 0; i < cs.length; i++) {
            int u = cs[i] - 'a';
            if (cur.next[u] == null) return 0;
            
            cur = cur.next[u];
        }
        
        if (cur.end) return cnt[cur.id];
        
        return 0;
    }
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        
        int n = sc.nextInt();
        sc.nextLine();
        
        while (n-- > 0) {
            String s = sc.nextLine();
            
            String[] ss = s.split(" ");
            
            char op = ss[0].charAt(0);
            String str = ss[1];
            char[] cs = str.toCharArray();
            
            if (op == 'I') insert(cs);
            else if (op == 'Q') System.out.println(hashQuery(cs));
        }
    }
    
}

C++代码实现：

#include <iostream>
using namespace std;

const int N = (int) 1e5 + 2333;
// 记录每个以特定id对应字符结尾字符串的个数
int cnt[N];
// 记录插入字符到字典树的实时id
int idx;
// 记录操作的字符串
char str[N];

class TireNode
{
public:
    // 记录该字符是不是最后一个字符
    bool end;
    // 记录子结点
    TireNode* next[26] = {nullptr};
    // 记录以该字符结尾的id
    int id;
    
    TireNode () {}
    
    TireNode(int _id) {
        id = _id;
    }
};

class Tire 
{
public:
    //根结点
    TireNode* tire = new TireNode();
    
    //插入操作
    void insert(char* cs)
    {
        TireNode* cur = tire;
        for (int i = 0; cs[i] != '\0'; i++)
        {
            int u = cs[i] - 'a';
            //cout << u << endl;
            if (cur->next[u] == nullptr) cur->next[u] = new TireNode(++idx);
            cur = cur->next[u];
        }
        
        cur->end = true;
        cnt[cur->id]++;
    }
    
    //查询操作
    int hashQuery(char* cs)
    {
        TireNode* cur = tire;
        for (int i = 0; cs[i] != '\0'; i++)
        {
            int u = cs[i] - 'a';
            
            if (cur->next[u] == nullptr) return 0;
            
            cur = cur->next[u];
        }
        
        if (!cur->end) return 0;
        
        return cnt[cur->id];
    }
    
};


int main() 
{
    int n;
    cin >> n;
    Tire tireTree;
    while (n-- > 0)
    {
        char op[2];
        cin >> op >> str;
        
        if (op[0] == 'I') tireTree.insert(str);
        else if (op[0] == 'Q') cout << tireTree.hashQuery(str) << endl;

    }
    return 0;
}

3.5使用数组实现（竞赛常用）

简单的说一下吧，N为字符串的所有输入字符串的最大长度，所以字典树的结点个数最大为N，那么最多可能也就是有N个next数组，代码中nes二维数组表示对应着前面的next数组，只不过把所有的结点的next数组都集中在一起罢了，所以我们也可以使用编号为每一个结点分配next数组，剩余的idx等变量含义与上面以class方式实现代码中的意思是一样的。

Java代码：

import java.util.*;

class Main {
    private static final int N = (int) 1e5 + 2333;
    private static int[][] nes = new int[N][26];
    private static int[] cnt = new int[N];
    private static int idx;
    //插入操作
    private static void insert(char[] cs) {
        int p = 0;
        for (int i = 0; i < cs.length; i++) {
            int u = cs[i] - 'a';
            if (nes[p][u] == 0) nes[p][u] = ++idx;
            
            //更新p
            p = nes[p][u];
        }
        
        //对应字符串数量加1
        cnt[p]++;
    }
    
    //查询操作
    private static int query(char[] cs) {
        int p = 0;
        for (int i = 0; i < cs.length; i++) {
            int u = cs[i] - 'a';
            if (nes[p][u] == 0) return 0;   //代表没有找到，找到的字符串数量为0
            
            //更新p
            p = nes[p][u];
        }
        
        //找到了返回该字符串的数量
        return cnt[p];
    }
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        int n = sc.nextInt();
        sc.nextLine();
        while (n-- > 0) {
            String s = sc.nextLine();
            
            String[] ss = s.split(" ");
            
            char op = ss[0].charAt(0);
            String str = ss[1];
            char[] cs = str.toCharArray();
            
            if (op == 'I') insert(cs);
            else if (op == 'Q') System.out.println(query(cs));
        }
    }
}

C++实现版本：

#include <iostream>

using namespace std;

const int N = (int) 1e5 + 2333;

//使用纯数组实现
int idx;        //表示结点的编号
int nes[N][26]; //表示某个字母的next数组 记录该字母所在字符串下一个字符的编号，为0表示该字母为结束字母
int cnt[N];     //记录在nes[p][u]位置结尾字符的字符串数量（也就是某一个字符串插入在字典树的数量）
char str[N];   //记录需要插入或者查询的字符串


//插入字符串
void insert(char* str)
{
    int p = 0;
    for (int i = 0; str[i] != 0; i++)
    {
        //如果遇到\0表示字符已经结束了
        
        //获取字符在字母表的顺序
        int u = str[i] - 'a';
        if (nes[p][u] == 0) nes[p][u] = ++idx;
        
        //更新p
        p = nes[p][u];
    }
    
    
    //将当前字符串数量++
    cnt[p]++;
}

//查询字符串是否存在
int query(char* str)
{
    int p = 0;
    for (int i = 0; str[i] != 0; i++)
    {
        int u = str[i] - 'a';
        if (nes[p][u] == 0) return 0;   //即返回false的意思
        
        p = nes[p][u];
    }
    
    return cnt[p];
}

int main()
{
    int n;
    cin >> n;
    while (n-- > 0)
    {
        char op[2];
        cin >> op >> str;
        
        if (op[0] == 'I') insert(str);
        else if (op[0] == 'Q') cout << query(str) << endl;
    }
    return 0;
}

参考资料：

字典树(Trie)详解

力扣中的字典树：

剑指 Offer II 062. 实现前缀树

208. 实现 Trie (前缀树)

472. 连接词

676. 实现一个魔法字典

648. 单词替换

745. 前缀和后缀搜索

820. 单词的压缩编码

面试题 17.13. 恢复空格

剑指 Offer II 064. 神奇的字典

剑指 Offer II 063. 替换单词

剑指 Offer II 065. 最短的单词编码

2416. 字符串的前缀分数和

0-1字典树（传统字典树变形）

剑指 Offer II 067. 最大的异或

1707. 与数组中元素的最大异或值

哈希表+字典树

面试题 16.02. 单词频率

剑指 Offer II 066. 单词之和

剑指 Offer II 063. 替换单词

【版权声明】本文为华为云社区用户原创内容，转载时必须标注文章的来源（华为云社区）、文章链接、文章作者等基本信息， 否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
C++ Java 数据结构
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入