2026-01-24：数组元素分组。用go语言，给定一个整数数组 nums 和一个整数 k，判断能否把数组里的所有元素划分成若干个大小为 k 的子集合，要求每个子集合内部没有重复值，并且数组中的每个元素只能出现在一个子集合中。若存在满足这些条件的划分方案则返回 true，否则返回 false。

1 <= nums.length <= 100000。

1 <= nums[i] <= 100000。

1 <= k <= nums.length。

输入： nums = [1,2,3,4], k = 2。

输出： true。

解释：

一种可能的分组方式是分成 2 组：

组 1：[1, 2]

组 2：[3, 4]

每个组包含 k = 2 个不同的元素，并且所有元素都被恰好使用一次。

题目来自力扣3659。

过程描述

1. 检查数组长度是否能被 k 整除
   首先判断数组长度 n 是否能被 k 整除。
   如果 n % k != 0，则不可能划分成若干个大小为 k 的子集合，直接返回 false。

2. 统计每个数字的出现次数
   创建一个计数数组 cnt，长度是 nums 中的最大值加 1（为了用下标直接映射数字）。
   遍历数组 nums，对每个数字 x，增加 cnt[x] 的计数。

3. 检查某个数字出现次数是否过多
   在遍历并统计的过程中，对于每个 x，如果 cnt[x] 大于 n/k，则立刻返回 false。
   这是因为：

   • 一共要分成 n/k 组，每组 k 个不同的数字。
   • 如果某个数字出现的次数大于组数 n/k，那么必然至少有一组会出现两次这个数字，违反“每组内部无重复值”的条件。

4. 返回结果
   如果前面没有返回 false，则返回 true。
   注意：这里代码没有进一步验证是否存在具体的分组方案，只做了必要条件的判断。
   对于本题的约束条件（数字范围有限，且出现次数不超过 n/k），数学上可以证明必然存在一种分组方案，因此代码只需做上述检查即可。

时间复杂度分析

• 遍历数组统计最大值：O(n)。
• 创建计数数组并初始化（Go 中会自动零值初始化）：O(M)，其中 M = max(nums) + 1。
• 遍历数组统计频次并检查 cnt[x] > n/k：O(n)。
  总时间复杂度：O(n + M)，其中 M 是数组中最大元素的值加 1（最大 100001）。

额外空间复杂度分析

• 主要额外空间是计数数组 cnt，大小为 M = max(nums) + 1。
  所以额外空间复杂度：O(M)，其中 M ≤ 100001。

Go完整代码如下：

package main

import (
	"fmt"
	"slices"
)

func partitionArray(nums []int, k int) bool {
	n := len(nums)
	if n%k > 0 {
		return false
	}
	cnt := make([]int, slices.Max(nums)+1)
	for _, x := range nums {
		cnt[x]++
		if cnt[x] > n/k {
			return false
		}
	}
	return true
}

func main() {
	nums := []int{1, 2, 3, 4}
	k := 2
	result := partitionArray(nums, k)
	fmt.Println(result)
}

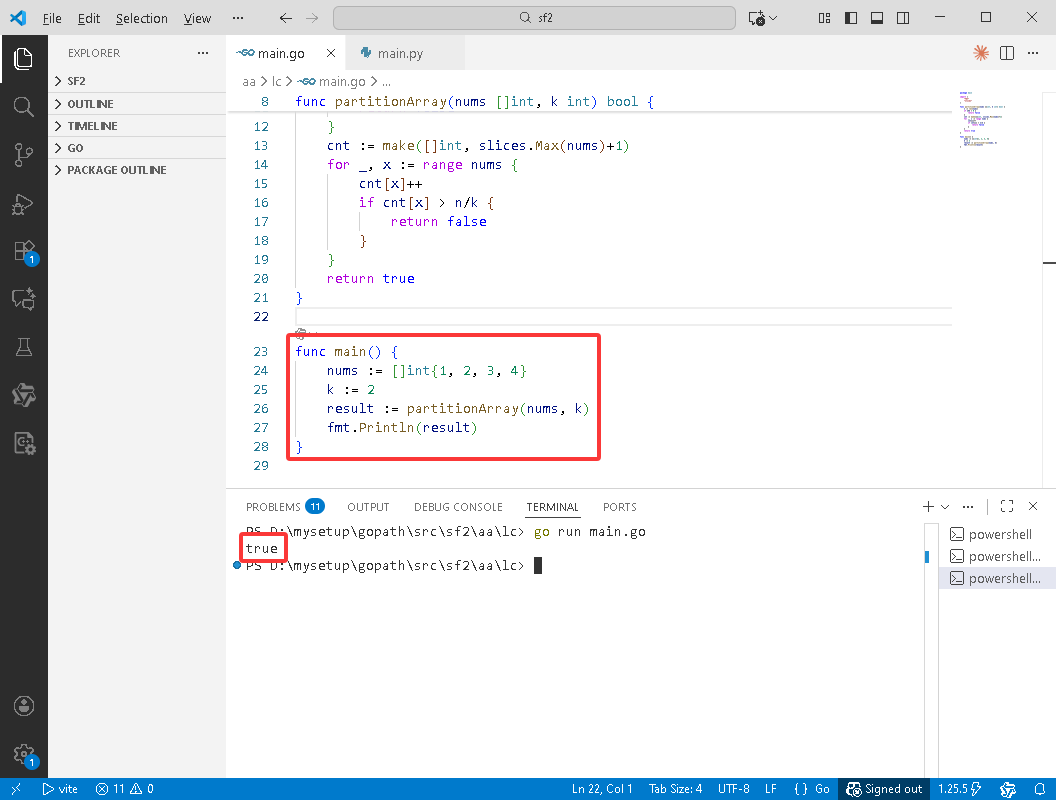
Python完整代码如下：

# -*-coding:utf-8-*-

def partitionArray(nums, k):
    n = len(nums)
    if n % k > 0:
        return False
    
    max_val = max(nums)
    cnt = [0] * (max_val + 1)
    
    for x in nums:
        cnt[x] += 1
        if cnt[x] > n // k:
            return False
    
    return True

# 测试用例
nums = [1, 2, 3, 4]
k = 2
result = partitionArray(nums, k)
print(result)

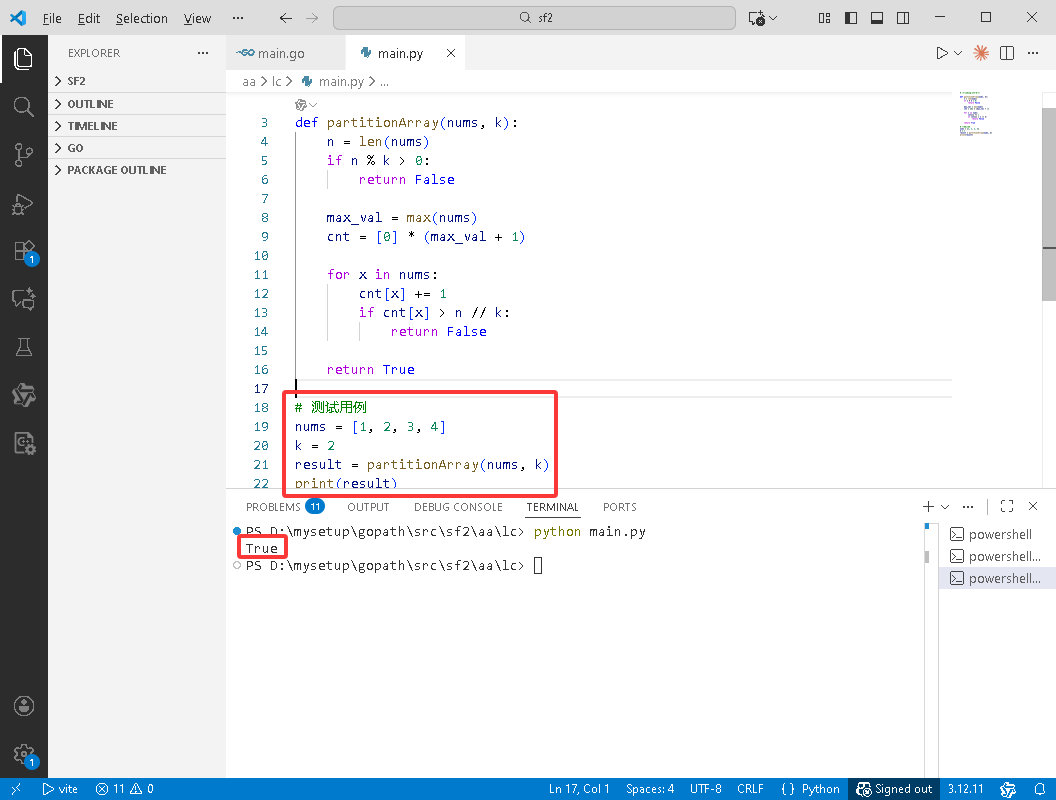
C++完整代码如下：

#include <iostream>
#include <vector>
#include <algorithm>

bool partitionArray(std::vector<int>& nums, int k) {
    int n = nums.size();
    if (n % k > 0) {
        return false;
    }

    int maxVal = *std::max_element(nums.begin(), nums.end());
    std::vector<int> cnt(maxVal + 1, 0);

    for (int x : nums) {
        cnt[x]++;
        if (cnt[x] > n / k) {
            return false;
        }
    }

    return true;
}

int main() {
    std::vector<int> nums = {1, 2, 3, 4};
    int k = 2;
    bool result = partitionArray(nums, k);
    std::cout << (result ? "true" : "false") << std::endl;
    return 0;
}