2026-01-20:按策略买卖股票的最佳时机。用go语言,给出两个等长整数数组 prices 和 strategy: - pr
2026-01-20:按策略买卖股票的最佳时机。用go语言,给出两个等长整数数组 prices 和 strategy:
-
prices[i] 表示第 i 天的股票价格;
-
strategy[i] 表示第 i 天的操作:-1 为买入一股,0 为不操作,1 为卖出一股。
还有一个偶数 k。你可以选择是否进行一次修改操作(也可以不改)。一次修改的规则是:选定 strategy 中恰好长度为 k 的一段连续位置,把这段的前 k/2 个位置全部改为 0(不操作),把后 k/2 个位置全部改为 1(卖出)。利润按所有天数 strategy[i] * prices[i] 的和来计算。
在遵循上述规则的前提下,求最多能得到的利润。提示:买卖次数、持股数量等没有限制,因此每天的买入或卖出在任何时候都是允许的。
2 <= prices.length == strategy.length <= 100000。
1 <= prices[i] <= 100000。
-1 <= strategy[i] <= 1。
2 <= k <= prices.length。
k 是偶数。
输入: prices = [5,4,3], strategy = [1,1,0], k = 2。
输出: 9。
解释:
| 修改 | 策略 | 利润计算 | 利润 |
|---|---|---|---|
| 原始 | [1, 1, 0] |
(1 × 5) + (1 × 4) + (0 × 3) = 5 + 4 + 0 | 9 |
| 修改 [0, 1] | [0, 1, 0] |
(0 × 5) + (1 × 4) + (0 × 3) = 0 + 4 + 0 | 4 |
| 修改 [1, 2] | [1, 0, 1] |
(1 × 5) + (0 × 4) + (1 × 3) = 5 + 0 + 3 | 8 |
因此,最大可能利润是 9,无需任何修改即可达成。
题目来自力扣3652。
算法执行过程分析
1. 初始化阶段
算法首先创建两个前缀和数组:
- profitSum数组:记录原始策略的累计利润。
profitSum[i+1]表示前i天按照原始策略操作的总利润 - priceSum数组:记录股票价格的累计和。
priceSum[i+1]表示前i天的股票价格总和
这两个数组的构建都采用前缀和技巧,通过一次遍历完成初始化。
2. 计算原始利润
算法首先计算不进行任何修改时的基础利润 res = profitSum[n],这是整个计算过程的基准值。
3. 枚举所有可能的修改区间
接下来,算法遍历所有可能的修改位置:
- 循环范围:从
i = k-1到n-1,共n-k+1次迭代 - 修改区间:每次迭代处理的是区间
[i-k+1, i](长度为k)
对于每个候选修改区间,算法计算三部分利润之和:
3.1 左侧利润(leftProfit)
profitSum[i-k+1]表示修改区间之前的日子按照原始策略操作的利润,这部分保持不变。
3.2 修改区间的利润(changeProfit)
这是最关键的计算部分:
- 前k/2天:策略改为0(不操作),利润为0
- 后k/2天:策略改为1(卖出),利润为这些天的价格之和
通过 priceSum[i+1] - priceSum[i-k/2+1] 巧妙计算出后k/2天的价格总和。
3.3 右侧利润(rightProfit)
profitSum[n] - profitSum[i+1]表示修改区间之后的日子按照原始策略操作的利润。
4. 利润比较与更新
对于每个候选修改区间,计算三部分利润之和,并与当前最大值res比较,更新最大值。
5. 返回最终结果
遍历完所有可能的修改区间后,返回找到的最大利润值。
复杂度分析
时间复杂度:O(n)
- 初始化两个前缀和数组:O(n)
- 遍历所有可能的修改区间:O(n-k+1) ≈ O(n)
- 每次区间操作都是常数时间O(1)
总时间复杂度为O(n),对于n最大为100000的数据规模是高效的。
空间复杂度:O(n)
- profitSum数组:O(n)
- priceSum数组:O(n)
总空间复杂度为O(n),主要是两个前缀和数组的存储开销。
这个算法通过巧妙运用前缀和技巧,将原本可能需要O(n²)时间复杂度的暴力解法优化到了O(n)级别,是典型的前缀和优化应用。
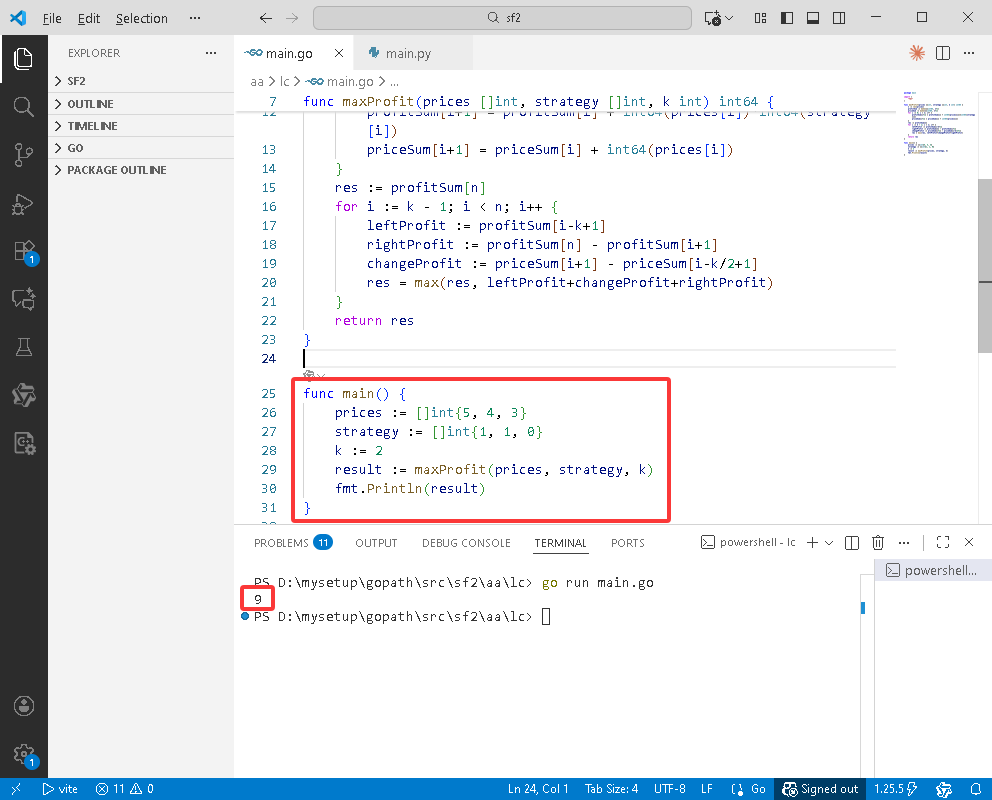
Go完整代码如下:
package main
import (
"fmt"
)
func maxProfit(prices []int, strategy []int, k int) int64 {
n := len(prices)
profitSum := make([]int64, n+1)
priceSum := make([]int64, n+1)
for i := 0; i < n; i++ {
profitSum[i+1] = profitSum[i] + int64(prices[i])*int64(strategy[i])
priceSum[i+1] = priceSum[i] + int64(prices[i])
}
res := profitSum[n]
for i := k - 1; i < n; i++ {
leftProfit := profitSum[i-k+1]
rightProfit := profitSum[n] - profitSum[i+1]
changeProfit := priceSum[i+1] - priceSum[i-k/2+1]
res = max(res, leftProfit+changeProfit+rightProfit)
}
return res
}
func main() {
prices := []int{5, 4, 3}
strategy := []int{1, 1, 0}
k := 2
result := maxProfit(prices, strategy, k)
fmt.Println(result)
}
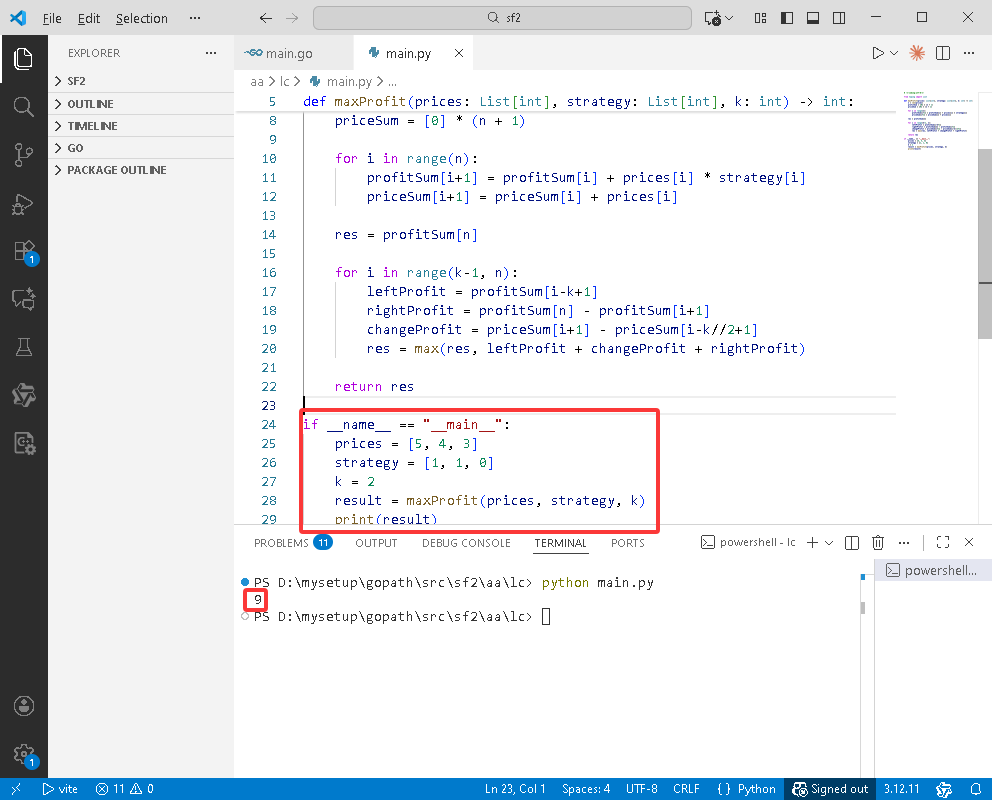
Python完整代码如下:
# -*-coding:utf-8-*-
from typing import List
def maxProfit(prices: List[int], strategy: List[int], k: int) -> int:
n = len(prices)
profitSum = [0] * (n + 1)
priceSum = [0] * (n + 1)
for i in range(n):
profitSum[i+1] = profitSum[i] + prices[i] * strategy[i]
priceSum[i+1] = priceSum[i] + prices[i]
res = profitSum[n]
for i in range(k-1, n):
leftProfit = profitSum[i-k+1]
rightProfit = profitSum[n] - profitSum[i+1]
changeProfit = priceSum[i+1] - priceSum[i-k//2+1]
res = max(res, leftProfit + changeProfit + rightProfit)
return res
if __name__ == "__main__":
prices = [5, 4, 3]
strategy = [1, 1, 0]
k = 2
result = maxProfit(prices, strategy, k)
print(result)
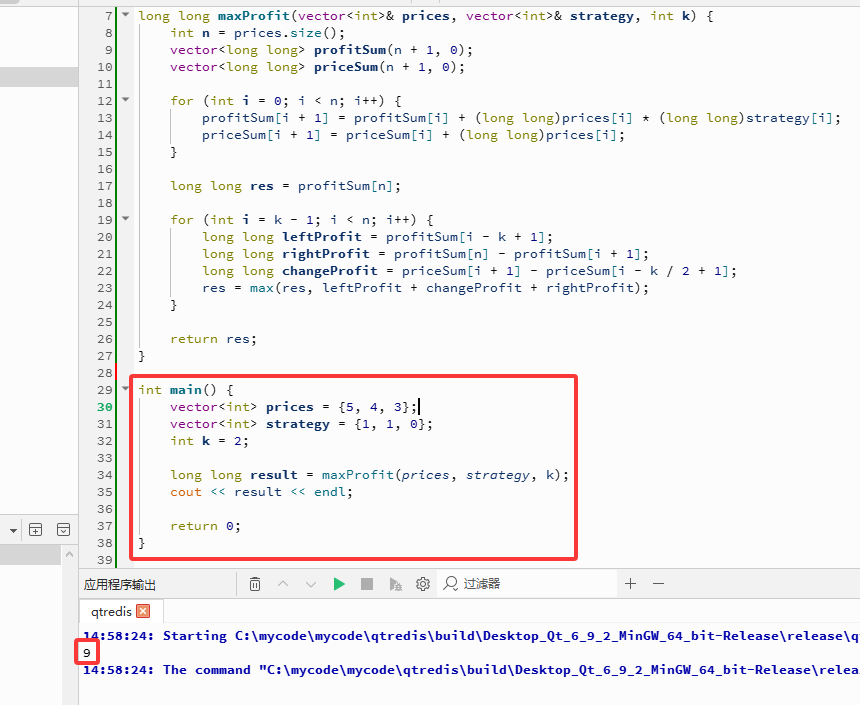
C++完整代码如下:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
long long maxProfit(vector<int>& prices, vector<int>& strategy, int k) {
int n = prices.size();
vector<long long> profitSum(n + 1, 0);
vector<long long> priceSum(n + 1, 0);
for (int i = 0; i < n; i++) {
profitSum[i + 1] = profitSum[i] + (long long)prices[i] * (long long)strategy[i];
priceSum[i + 1] = priceSum[i] + (long long)prices[i];
}
long long res = profitSum[n];
for (int i = k - 1; i < n; i++) {
long long leftProfit = profitSum[i - k + 1];
long long rightProfit = profitSum[n] - profitSum[i + 1];
long long changeProfit = priceSum[i + 1] - priceSum[i - k / 2 + 1];
res = max(res, leftProfit + changeProfit + rightProfit);
}
return res;
}
int main() {
vector<int> prices = {5, 4, 3};
vector<int> strategy = {1, 1, 0};
int k = 2;
long long result = maxProfit(prices, strategy, k);
cout << result << endl;
return 0;
}
- 点赞
- 收藏
- 关注作者


评论(0)