2026-01-02:插入一个字母的最大子序列数。用go语言,给定一个只含大写字母的字符串 s。你可以选择是否在字符串中加入最多
【摘要】 2026-01-02:插入一个字母的最大子序列数。用go语言,给定一个只含大写字母的字符串 s。你可以选择是否在字符串中加入最多一个额外的大写字母,插入位置可以放在任意位置(包括开头或结尾)。目标是使结果字符串中能够形成尽可能多的 “LCT” 模式——也就是选出下标 i<j<k,使得对应字符依次为 ‘L’、‘C’、‘T’(等价于从字符串中删去若干字符但保持剩余字符相对顺序后得到 “LCT”)...
2026-01-02:插入一个字母的最大子序列数。用go语言,给定一个只含大写字母的字符串 s。你可以选择是否在字符串中加入最多一个额外的大写字母,插入位置可以放在任意位置(包括开头或结尾)。目标是使结果字符串中能够形成尽可能多的 “LCT” 模式——也就是选出下标 i<j<k,使得对应字符依次为 ‘L’、‘C’、‘T’(等价于从字符串中删去若干字符但保持剩余字符相对顺序后得到 “LCT”)。求在最优的插入选择下,最终能得到的 “LCT” 出现次数的最大值。
1 <= s.length <= 100000。
s 仅由大写英文字母组成。
输入: s = “LMCT”。
输出: 2。
解释:
可以在字符串 s 的开头插入一个 “L”,变为 “LLMCT”,其中包含 2 个子序列,分别位于下标 [0, 3, 4] 和 [1, 3, 4]。
题目来自力扣3628。
算法步骤分析
1. 统计字符’T’的数量
算法首先统计原始字符串中字符’T’的总数,这个值会在后续计算中用于评估某些插入策略的潜力。
2. 遍历字符串并计算关键指标
算法逐个字符遍历字符串,同时维护多个关键计数器:
- 基础计数器:
l统计遇到的’L’数量,c统计遇到的’C’数量 - 组合计数器:
lc统计已形成的"LC"组合数量,lct统计已形成的"LCT"子序列数量 - 插入相关计数器:
ct统计’C’后面’T’的数量组合,lt评估’L’和’T’的搭配潜力
3. 动态更新计数器
对于每个字符的处理:
- 遇到’L’:
l计数器增加 - 遇到’C’:
lc增加当前已存在的’L’数量(因为每个已存在的’L’都能与这个’C’形成新的"LC"组合),同时c计数器增加 - 遇到’T’:
lct增加当前已存在的"LC"组合数量(每个"LC"都能与这个’T’形成完整的"LCT"),ct增加当前已存在的’C’数量,同时减少剩余’T’数量的统计
4. 评估插入策略
算法通过max(ct, lc, lt)来评估三种最优插入策略:
- 插入’C’:
ct代表在’C’位置插入后能新增的"LCT"数量 - 插入’T’:
lc代表在’T’位置插入后能新增的"LCT"数量 - 插入’L’:
lt代表在’L’位置插入后能新增的"LCT"数量
5. 计算结果
最终结果是原始字符串中的"LCT"子序列数量lct加上最优插入策略能带来的最大增量。
复杂度分析
时间复杂度:O(n)
- 算法只需要单次遍历字符串,每个字符的处理都是常数时间操作
- 其中n为字符串s的长度
空间复杂度:O(1)
- 算法只使用了固定数量的整型变量作为计数器,不随输入规模增长而增加额外空间
- 这些变量的空间占用是常数级别的
Go完整代码如下:
package main
import (
"fmt"
"strings"
)
func numOfSubsequences(s string) int64 {
t := strings.Count(s, "T")
var l, lc, lct, c, ct, lt int
for _, b := range s {
if b == 'L' {
l++
} else if b == 'C' {
lc += l
c++
} else if b == 'T' {
lct += lc
ct += c
t--
}
lt = max(lt, l*t)
}
return int64(lct + max(ct, lc, lt))
}
func main() {
s := "LMCT"
result := numOfSubsequences(s)
fmt.Println(result)
}
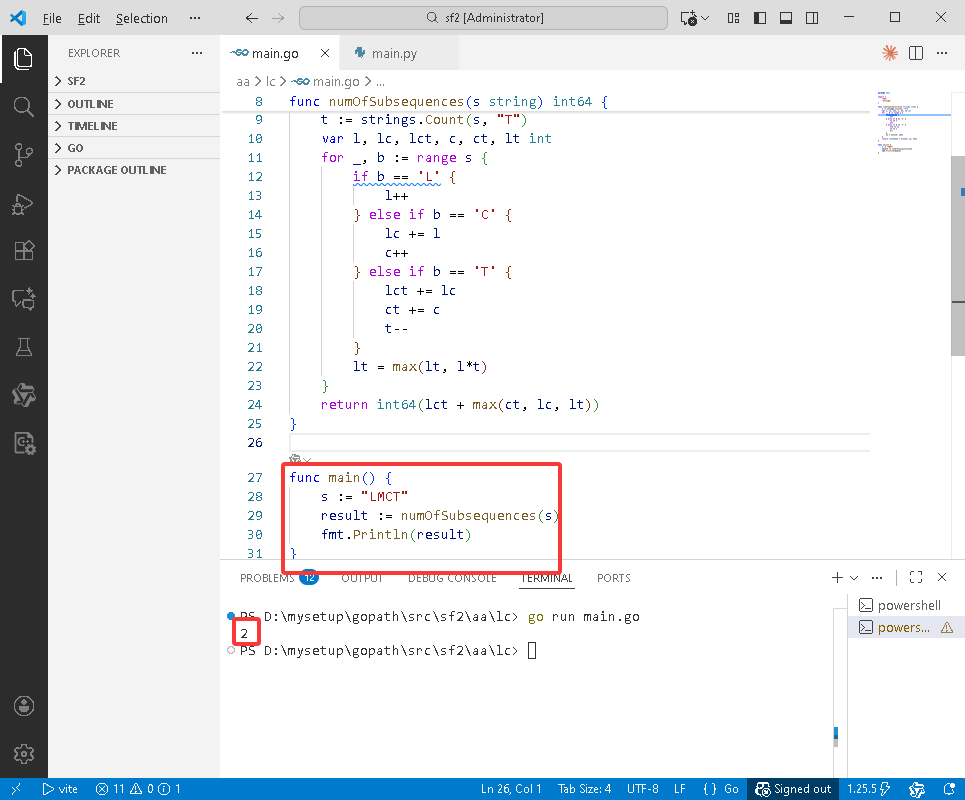
Python完整代码如下:
# -*-coding:utf-8-*-
def numOfSubsequences(s: str) -> int:
t = s.count('T')
l = lc = lct = c = ct = lt = 0
for ch in s:
if ch == 'L':
l += 1
elif ch == 'C':
lc += l
c += 1
elif ch == 'T':
lct += lc
ct += c
t -= 1
lt = max(lt, l * t)
return lct + max(ct, lc, lt)
# 测试代码
if __name__ == "__main__":
s = "LMCT"
result = numOfSubsequences(s)
print(result)
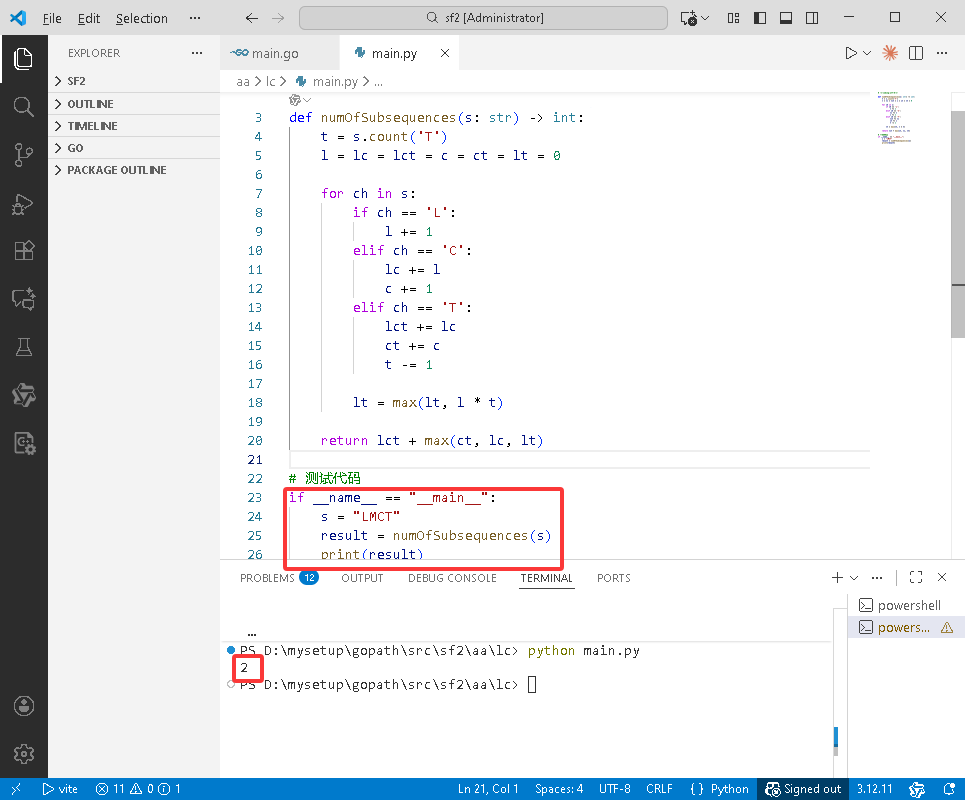
C++完整代码如下:
#include <iostream>
#include <string>
#include <algorithm>
#include <cstdint>
int64_t numOfSubsequences(const std::string& s) {
int t = std::count(s.begin(), s.end(), 'T');
int l = 0, lc = 0, lct = 0, c = 0, ct = 0, lt = 0;
for (char ch : s) {
if (ch == 'L') {
l++;
} else if (ch == 'C') {
lc += l;
c++;
} else if (ch == 'T') {
lct += lc;
ct += c;
t--;
}
lt = std::max(lt, l * t);
}
return lct + std::max({ct, lc, lt});
}
int main() {
std::string s = "LMCT";
int64_t result = numOfSubsequences(s);
std::cout << result << std::endl;
return 0;
}
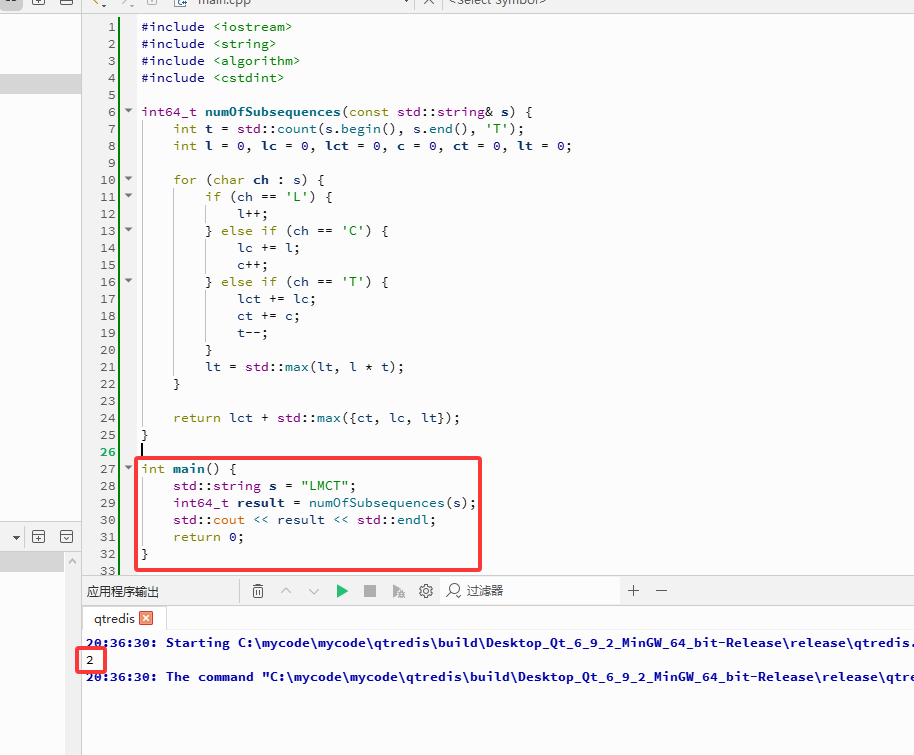
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)