2025-12-30：统计梯形的数目Ⅰ。用go语言，给定一组平面上的整数坐标点 points，其中每个元素 points[i] = [xi, yi] 表示第 i 个点的位置。要求统计有多少种从这些点中选出四个互不相同的点，使它们可以按某种顺序连成一个凸的四边形，并且该四边形至少存在一对水平的边（也就是有两条边平行于 x 轴）。注意如果两条直线的斜率相同则称它们平行。因为结果可能很大，请将最终计数对 1000000007 取余后返回。

4 <= points.length <= 100000。

–100000000 <= xi, yi <= 100000000。

所有点两两不同。

输入： points = [[1,0],[2,0],[3,0],[2,2],[3,2]]。

输出： 3。

解释：

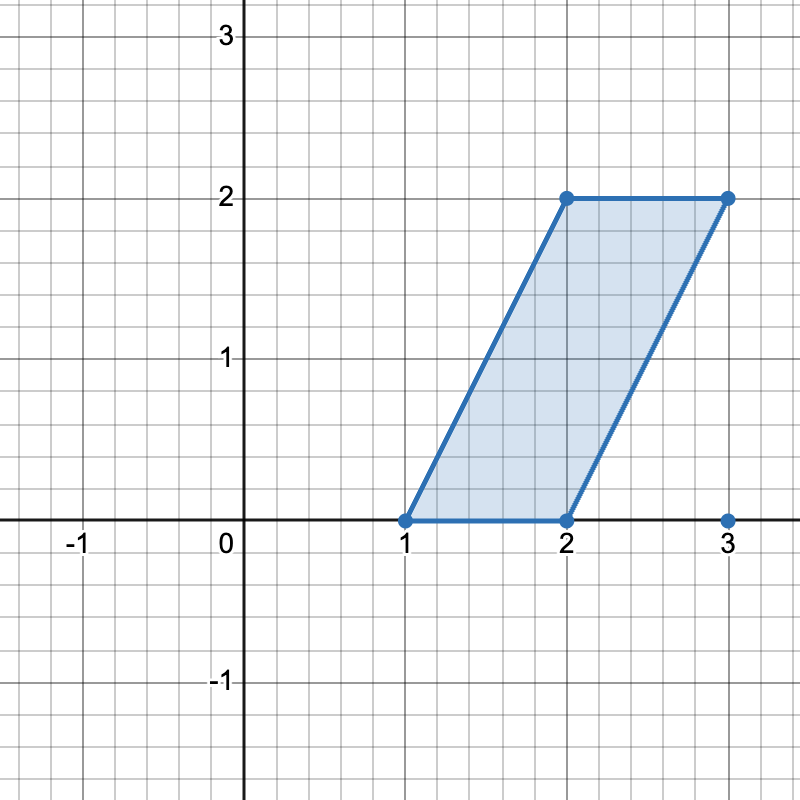
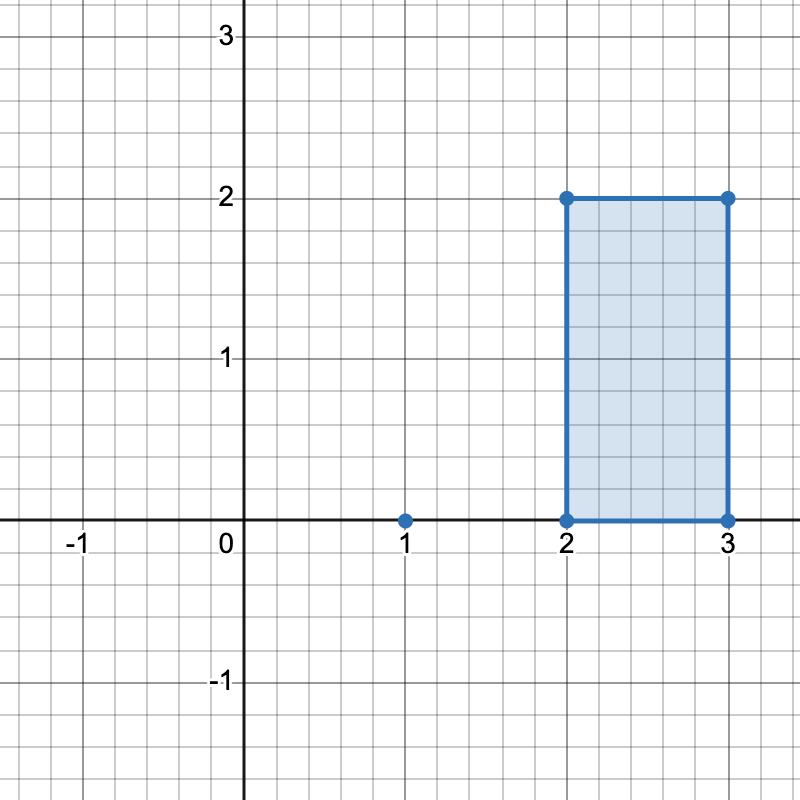
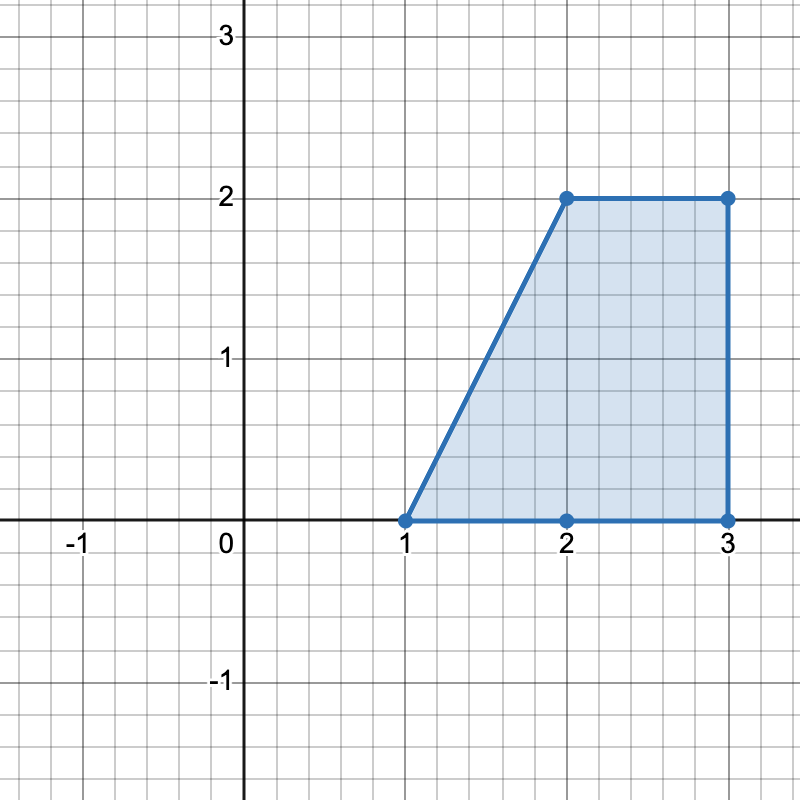
有三种不同方式选择四个点组成一个水平梯形：

使用点 [1,0]、[2,0]、[3,2] 和 [2,2]。

使用点 [2,0]、[3,0]、[3,2] 和 [2,2]。

使用点 [1,0]、[3,0]、[3,2] 和 [2,2]。

题目来自力扣3623。

算法过程详解

1. 按y坐标分组计数
   算法首先遍历整个点集 points，目的是统计出有多少个点位于同一水平线（即y坐标相同）上。这是通过一个哈希表 pointNum 实现的，其键（key）是y坐标值，值（value）是对应y坐标上点的数量。例如，对于输入点集 [[1,0],[2,0],[3,0],[2,2],[3,2]]，遍历后得到的哈希表内容将是 {0: 3, 2: 2}，表示y=0的水平线上有3个点，y=2的水平线上有2个点。

2. 计算每条水平线的边对数
   接下来，算法处理哈希表 pointNum 中的每一组计数。对于一个包含 pNum 个点的水平线，从中任意选择两个点都可以形成一条水平的边。根据组合数学公式，选择两个点的组合数（即边对数）为 C(pNum, 2) = pNum * (pNum - 1) / 2。

   • 在上面的例子中，y=0的点数为3，边对数 C(3,2) = 3。
   • y=2的点数为2，边对数 C(2,2) = 1。

3. 组合不同水平线的边对以形成梯形
   一个水平梯形需要两条水平边，这两条边必须来自不同的水平线。因此，梯形的总数就是所有不同水平线的边对数两两相乘的总和。
   算法采用了一种高效的累加技巧来计算这个总和，避免了双重循环。

   • 它维护两个变量：ans（最终答案）和 sum（之前已经处理过的所有水平线的边对数之和）。
   • 在遍历每条水平线的边对数 edge 时，当前水平线可以与之前所有水平线形成 edge * sum 个梯形，将此值累加到 ans 中。
   • 然后，将当前水平线的边对数 edge 加到 sum 中，以便后续水平线使用。
   • 对于我们的例子：处理第一条水平线（y=0，edge=3）时，sum初始为0，所以ans累加0，然后sum变为3。处理第二条水平线（y=2，edge=1）时，ans累加 1 * 3 = 3，得到最终结果。

4. 取模运算
   由于结果可能非常大，题目要求对 1000000007 取模。算法在每次进行加法和乘法运算后都立即对中间结果取模，这是为了防止整数溢出并保证结果正确。

复杂度分析

• 总的时间复杂度：O(n)
  其中 n 是点的总数。算法主要包含两次顺序遍历：第一次遍历所有点（n个）进行分组计数，第二次遍历哈希表中的不同y坐标组（m个）。由于 m（不同y坐标的数量）最大可能为 n，但在一般情况下 m << n，整体操作次数与 n 成线性关系。

• 总的额外空间复杂度：O(m)
  其中 m 是不同y坐标的数量。算法使用了一个哈希表 pointNum 来存储每个y坐标对应的点数量，该哈希表最多需要存储 m 个键值对。除此之外，只使用了几个整型变量，因此额外的空间消耗主要由哈希表决定。

Go完整代码如下：

package main

import (
	"fmt"
)

func countTrapezoids(points [][]int) int {
	pointNum := make(map[int]int)
	mod := 1000000007
	ans, sum := 0, 0

	for _, point := range points {
		y := point[1]
		pointNum[y]++
	}

	for _, pNum := range pointNum {
		edge := pNum * (pNum - 1) / 2
		ans = (ans + edge*sum) % mod
		sum = (sum + edge) % mod
	}

	return ans
}

func main() {
	points := [][]int{{1, 0}, {2, 0}, {3, 0}, {2, 2}, {3, 2}}
	result := countTrapezoids(points)
	fmt.Println(result)
}

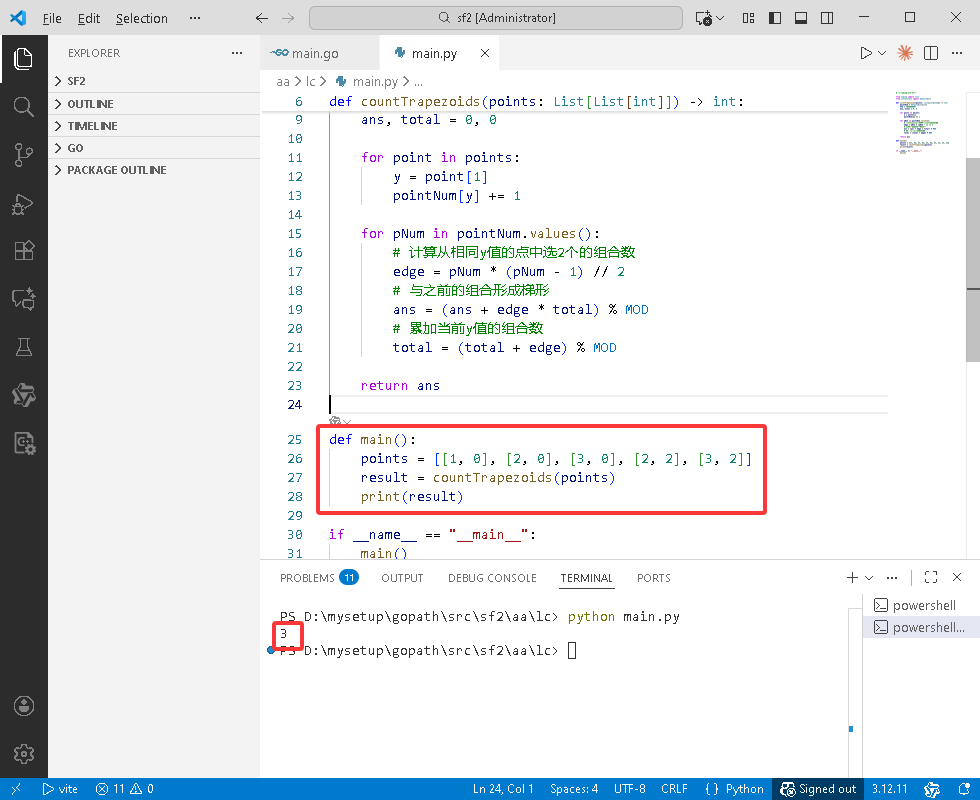
Python完整代码如下：

# -*-coding:utf-8-*-

from typing import List
from collections import defaultdict

def countTrapezoids(points: List[List[int]]) -> int:
    pointNum = defaultdict(int)
    MOD = 1000000007
    ans, total = 0, 0
    
    for point in points:
        y = point[1]
        pointNum[y] += 1
    
    for pNum in pointNum.values():
        # 计算从相同y值的点中选2个的组合数
        edge = pNum * (pNum - 1) // 2
        # 与之前的组合形成梯形
        ans = (ans + edge * total) % MOD
        # 累加当前y值的组合数
        total = (total + edge) % MOD
    
    return ans

def main():
    points = [[1, 0], [2, 0], [3, 0], [2, 2], [3, 2]]
    result = countTrapezoids(points)
    print(result)

if __name__ == "__main__":
    main()

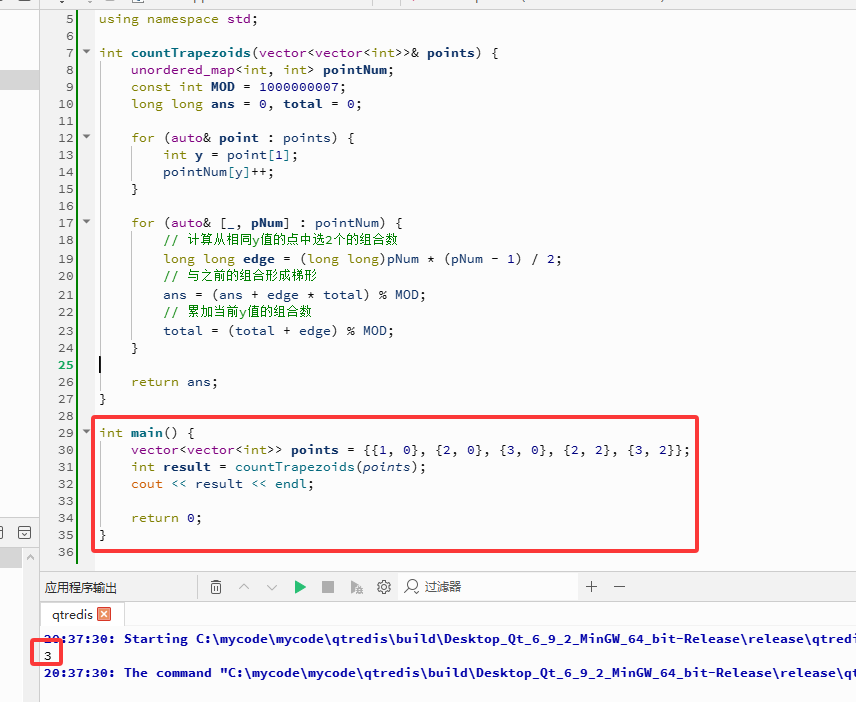
C++完整代码如下：

#include <iostream>
#include <vector>
#include <unordered_map>

using namespace std;

int countTrapezoids(vector<vector<int>>& points) {
    unordered_map<int, int> pointNum;
    const int MOD = 1000000007;
    long long ans = 0, total = 0;

    for (auto& point : points) {
        int y = point[1];
        pointNum[y]++;
    }

    for (auto& [_, pNum] : pointNum) {
        // 计算从相同y值的点中选2个的组合数
        long long edge = (long long)pNum * (pNum - 1) / 2;
        // 与之前的组合形成梯形
        ans = (ans + edge * total) % MOD;
        // 累加当前y值的组合数
        total = (total + edge) % MOD;
    }

    return ans;
}

int main() {
    vector<vector<int>> points = {{1, 0}, {2, 0}, {3, 0}, {2, 2}, {3, 2}};
    int result = countTrapezoids(points);
    cout << result << endl;

    return 0;
}