2025-12-16:数组的最小稳定性因子。用go语言,给定一个整数数组 nums 和一个整数 maxC。把满足以下条件的连续区
【摘要】 2025-12-16:数组的最小稳定性因子。用go语言,给定一个整数数组 nums 和一个整数 maxC。把满足以下条件的连续区间称为“稳定子数组”:区间内所有数的最大公约数(GCD)至少为 2。定义数组的“稳定性因子”为其最长稳定子数组的长度。你可以最多对数组中的 maxC 个位置改成任意整数。问题是:在不超过 maxC 次修改后,能够把稳定性因子降到多小?返回这个最小可能的稳定性因子;如...
2025-12-16:数组的最小稳定性因子。用go语言,给定一个整数数组 nums 和一个整数 maxC。把满足以下条件的连续区间称为“稳定子数组”:区间内所有数的最大公约数(GCD)至少为 2。
定义数组的“稳定性因子”为其最长稳定子数组的长度。你可以最多对数组中的 maxC 个位置改成任意整数。问题是:在不超过 maxC 次修改后,能够把稳定性因子降到多小?返回这个最小可能的稳定性因子;如果最终不存在任何稳定子数组,则返回 0。
补充说明:
-
子数组指数组的连续片段。
-
数组的最大公约数指能同时整除所有元素的最大整数。
-
长度为 1 的子数组若其唯一元素 ≥ 2,也视为稳定子数组。
1 <= n == nums.length <= 100000。
1 <= nums[i] <= 1000000000。
0 <= maxC <= n。
输入:nums = [3,5,10], maxC = 1。
输出:1。
解释:
稳定的子数组 [5, 10] 的 HCF = 5,其稳定性因子为 2。
由于 maxC = 1,一个最优策略是将 nums[1] 改为 7,得到 nums = [3, 7, 10]。
现在,没有长度大于 1 的子数组的 HCF >= 2。因此,最小可能稳定性因子是 1。
题目来自力扣3605。
🔍 算法步骤详解
-
初始化与预处理
- 函数首先获取数组长度
n,并初始化一个与nums等长的切片leftMin。这个切片用于记录一个关键信息:对于每个位置i,leftMin[i]表示以i为区间右端点时,能够使得区间内所有元素的最大公约数(GCD)大于等于2的、最靠左的起点位置。 - 变量
left和bottom初始化为0,它们共同维护一个滑动窗口或处理区间。rightGcd初始化为0(因为任何数与0的GCD是其本身)。
- 函数首先获取数组长度
-
计算 leftMin 数组
- 这是算法的核心步骤。它通过一次遍历(下标
i从0到n-1)来计算leftMin数组。 - 更新GCD:对于当前元素
nums[i],代码通过rightGcd = gcd(rightGcd, nums[i])来累积计算从某个起点到i的整个区间的GCD。 - 收缩左边界:使用一个内层循环(
for left <= i && gcd(nums[left], rightGcd) == 1)来调整左边界left。这个条件的目的是检查当前窗口[left, i]的GCD是否因为包含了nums[left]而变为1(即不满足稳定子数组条件)。如果变为1,就需要向右移动left指针,直到窗口内的GCD再次大于等于2,或者窗口为空。 - 记录左边界:将最终确定的左边界
left记录到leftMin[i]中。 - 栈式重建(关键优化):当需要移动
left指针,并且bottom(可以理解为上一次重建的起始点)小于或等于当前的left时,会触发一个重建操作。这个操作从i-1到left+1逆序地重新计算区间GCD,这类似于维护一个隐式的栈结构,用于高效地更新GCD信息,避免每次都从头计算。完成后,bottom被更新为i,rightGcd重置为0。
- 这是算法的核心步骤。它通过一次遍历(下标
-
二分查找最小稳定性因子
- 在得到
leftMin数组后,算法使用二分搜索来确定最小的稳定性因子(即最长稳定子数组的长度上限upper)。 - 搜索范围:二分查找的下界是0,上界可以设为
n/(maxC+1),这是一个合理的估计,因为修改maxC个点最多能将数组分成maxC+1段。 - 检查函数:对于每一个候选的
upper值,函数模拟修改操作,检查是否能在最多maxC次修改后,使得数组中所有稳定子数组的长度都不超过upper。 - 贪心模拟:检查过程采用贪心策略。从左到右遍历数组,当遇到一个稳定子数组的长度超过
upper时(即i - leftMin[i] + 1 > upper),就在这个子数组的末尾之后进行一次“修改”(实际上是通过将索引i跳转upper + 1位来模拟),并消耗一次修改次数。如果修改次数在遍历完数组前用完,则说明当前upper值太小,需要增大;否则,说明upper值可行,可以尝试更小的值。
- 在得到
-
返回结果
- 二分查找结束后,找到的最小满足条件的
upper值就是题目要求的最小可能稳定性因子,将其返回。
- 二分查找结束后,找到的最小满足条件的
⏱ 复杂度分析
时间复杂度
- 计算
leftMin数组:主循环遍历每个元素一次。虽然内部有循环和重建操作,但每个元素最多被加入和移出“栈”一次,GCD计算可以看作是常数时间(因为整数大小有限,GCD操作很快)。因此,这部分的时间复杂度可以看作是 O(n)。 - 二分查找与检查:二分查找的迭代次数是 O(log n)。每次检查需要遍历整个数组,是 O(n)。所以这部分的总时间复杂度是 O(n log n)。
- 综合:整个算法的总时间复杂度为 O(n log n)。
空间复杂度
- 算法主要使用了
leftMin数组,其大小为 O(n)。 - 其他变量如
left,bottom,rightGcd等占用常数空间。 - 在计算GCD的递归或栈模拟过程中,没有使用与输入规模成比例的额外数据结构。
- 因此,算法的总额外空间复杂度为 O(n)。
Go完整代码如下:
package main
import (
"fmt"
"sort"
)
func minStable(nums []int, maxC int) int {
n := len(nums)
leftMin := make([]int, n)
var left, bottom, rightGcd int
for i, x := range nums {
rightGcd = gcd(rightGcd, x)
for left <= i && gcd(nums[left], rightGcd) == 1 {
if bottom <= left {
// 重新构建一个栈
// 由于 left 即将移出窗口,只需计算到 left+1
for j := i - 1; j > left; j-- {
nums[j] = gcd(nums[j], nums[j+1])
}
bottom = i
rightGcd = 0
}
left++
}
leftMin[i] = left
}
ans := sort.Search(n/(maxC+1), func(upper int) bool {
c := maxC
i := upper
for i < n {
if i-leftMin[i]+1 > upper {
if c == 0 {
return false
}
c--
i += upper + 1
} else {
i++
}
}
return true
})
return ans
}
func gcd(a, b int) int {
for a != 0 {
a, b = b%a, a
}
return b
}
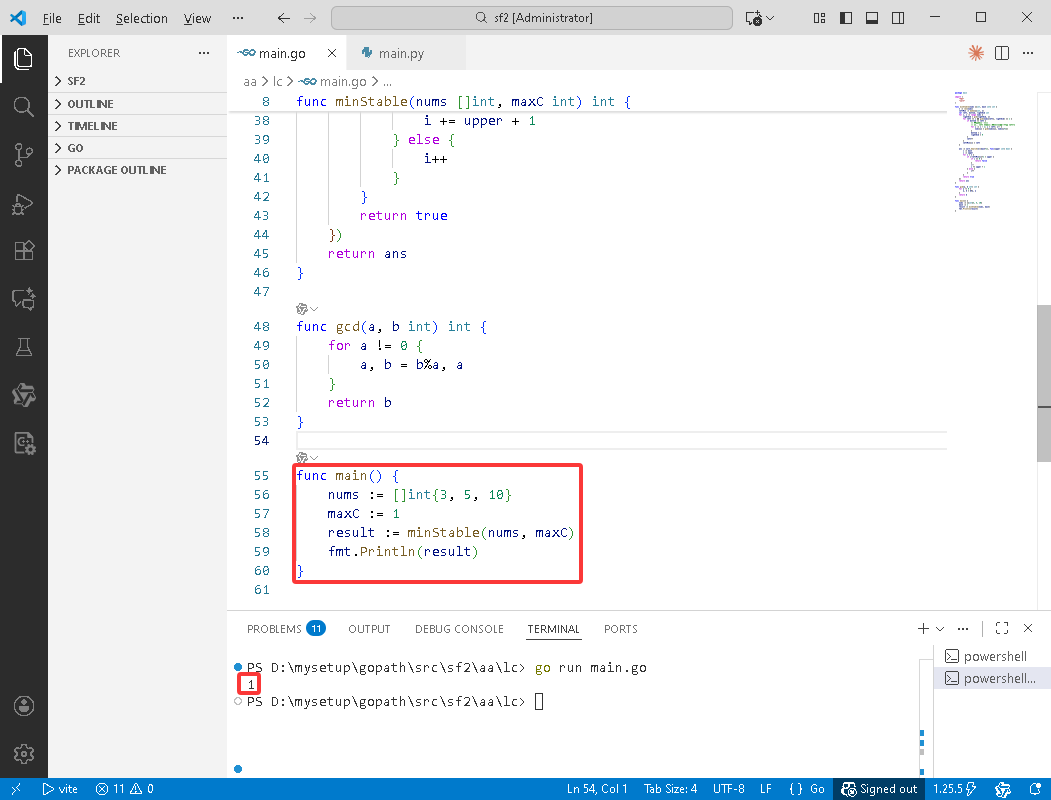
func main() {
nums := []int{3, 5, 10}
maxC := 1
result := minStable(nums, maxC)
fmt.Println(result)
}
Python完整代码如下:
# -*-coding:utf-8-*-
import math
from typing import List
import bisect
def minStable(nums: List[int], maxC: int) -> int:
n = len(nums)
leftMin = [0] * n
left = 0
bottom = 0
rightGcd = 0
for i in range(n):
x = nums[i]
rightGcd = math.gcd(rightGcd, x)
while left <= i and math.gcd(nums[left], rightGcd) == 1:
if bottom <= left:
# 重新构建一个栈
# 由于 left 即将移出窗口,只需计算到 left+1
for j in range(i - 1, left, -1):
nums[j] = math.gcd(nums[j], nums[j + 1])
bottom = i
rightGcd = 0
left += 1
leftMin[i] = left
# 二分查找
def check(upper: int) -> bool:
c = maxC
i = upper
while i < n:
if i - leftMin[i] + 1 > upper:
if c == 0:
return False
c -= 1
i += upper + 1
else:
i += 1
return True
# 使用二分查找找到最小满足条件的值
low, high = 0, n // (maxC + 1) + 1
while low < high:
mid = (low + high) // 2
if check(mid):
high = mid
else:
low = mid + 1
return low
# 另一种更简洁的二分查找实现方式
def minStable_alternative(nums: List[int], maxC: int) -> int:
n = len(nums)
leftMin = [0] * n
left = 0
bottom = 0
rightGcd = 0
for i in range(n):
x = nums[i]
rightGcd = math.gcd(rightGcd, x)
while left <= i and math.gcd(nums[left], rightGcd) == 1:
if bottom <= left:
# 重新构建一个栈
for j in range(i - 1, left, -1):
nums[j] = math.gcd(nums[j], nums[j + 1])
bottom = i
rightGcd = 0
left += 1
leftMin[i] = left
# 使用 Python 的 bisect 风格二分查找
ans = bisect.bisect_left(range(n // (maxC + 1) + 1), True, key=lambda upper: check(upper))
def check(upper: int) -> bool:
c = maxC
i = upper
while i < n:
if i - leftMin[i] + 1 > upper:
if c == 0:
return False
c -= 1
i += upper + 1
else:
i += 1
return True
return ans
# 测试代码
if __name__ == "__main__":
nums = [3, 5, 10]
maxC = 1
result = minStable(nums, maxC)
print(f"minStable result: {result}")
# 测试更多用例
test_cases = [
([3, 5, 10], 1),
([2, 3, 4, 5], 2),
([1, 2, 3, 4, 5], 1),
([6, 10, 15], 0),
]
for nums, maxC in test_cases:
result = minStable(nums.copy(), maxC)
print(f"nums={nums}, maxC={maxC} -> result={result}")
C++完整代码如下:
#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>
#include <numeric>
using namespace std;
int gcd(int a, int b) {
while (a != 0) {
int temp = a;
a = b % a;
b = temp;
}
return b;
}
int minStable(vector<int>& nums, int maxC) {
int n = nums.size();
vector<int> leftMin(n, 0);
int left = 0, bottom = 0, rightGcd = 0;
for (int i = 0; i < n; i++) {
int x = nums[i];
rightGcd = gcd(rightGcd, x);
while (left <= i && gcd(nums[left], rightGcd) == 1) {
if (bottom <= left) {
// 重新构建一个栈
// 由于 left 即将移出窗口,只需计算到 left+1
for (int j = i - 1; j > left; j--) {
nums[j] = gcd(nums[j], nums[j + 1]);
}
bottom = i;
rightGcd = 0;
}
left++;
}
leftMin[i] = left;
}
// 二分查找
auto check = [&](int upper) -> bool {
int c = maxC;
int i = upper;
while (i < n) {
if (i - leftMin[i] + 1 > upper) {
if (c == 0) {
return false;
}
c--;
i += upper + 1;
} else {
i++;
}
}
return true;
};
int low = 0, high = n / (maxC + 1) + 1;
while (low < high) {
int mid = low + (high - low) / 2;
if (check(mid)) {
high = mid;
} else {
low = mid + 1;
}
}
return low;
}
// 使用C++标准库的binary_search风格
int minStable2(vector<int>& nums, int maxC) {
int n = nums.size();
vector<int> leftMin(n, 0);
int left = 0, bottom = 0, rightGcd = 0;
for (int i = 0; i < n; i++) {
int x = nums[i];
rightGcd = gcd(rightGcd, x);
while (left <= i && gcd(nums[left], rightGcd) == 1) {
if (bottom <= left) {
// 重新构建一个栈
for (int j = i - 1; j > left; j--) {
nums[j] = gcd(nums[j], nums[j + 1]);
}
bottom = i;
rightGcd = 0;
}
left++;
}
leftMin[i] = left;
}
// 使用lower_bound风格的二分查找
vector<int> range(n / (maxC + 1) + 1);
for (int i = 0; i < range.size(); i++) {
range[i] = i;
}
auto it = lower_bound(range.begin(), range.end(), true,
[&](int upper, bool) {
int c = maxC;
int i = upper;
while (i < n) {
if (i - leftMin[i] + 1 > upper) {
if (c == 0) {
return true; // 返回true表示upper不够大
}
c--;
i += upper + 1;
} else {
i++;
}
}
return false; // 返回false表示upper足够大
});
return (it != range.end()) ? *it : n;
}
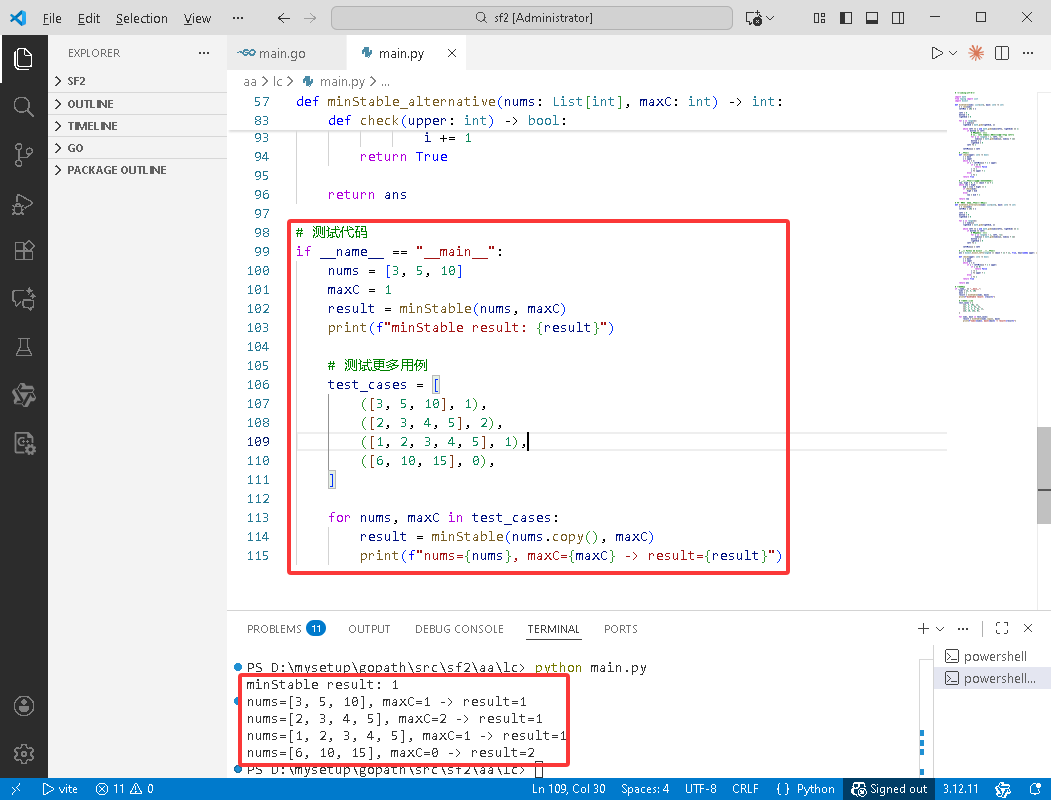
int main() {
vector<int> nums = {3, 5, 10};
int maxC = 1;
int result = minStable(nums, maxC);
cout << "minStable result: " << result << endl;
// 测试更多用例
vector<pair<vector<int>, int>> testCases = {
{{3, 5, 10}, 1},
{{2, 3, 4, 5}, 2},
{{1, 2, 3, 4, 5}, 1},
{{6, 10, 15}, 0},
};
for (auto& testCase : testCases) {
vector<int> numsCopy = testCase.first;
int maxC = testCase.second;
int result = minStable(numsCopy, maxC);
cout << "nums=[";
for (size_t i = 0; i < testCase.first.size(); i++) {
cout << testCase.first[i];
if (i < testCase.first.size() - 1) cout << ", ";
}
cout << "], maxC=" << maxC << " -> result=" << result << endl;
}
return 0;
}
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)