2025-12-15：有向图中到达终点的最少时间。用go语言，给出一个有向图和一个整数 n，图中节点编号为 0 到 n-1。每条边用四元组 edges[i] = [ui, vi, starti, endi] 描述，表示从 ui 指向 vi 的这条边只有在某些时刻可用：只有当当前的整数时刻 t 落在区间 [starti, endi]（含端点）时，才能沿该边移动。

你在时刻 0 位于节点 0。每经过一个单位时间，可以选择两种行为之一：

• 留在当前节点不动；

• 如果存在一条从当前节点出发的边，并且此时刻 t 在该边允许的时间区间内，则沿该有向边移动到相应的邻接节点。

求到达节点 n-1 所需的最小时间（以整数时刻计）。如果无法到达，返回 -1。

1 <= n <= 100000。

0 <= edges.length <= 100000。

edges[i] == [ui, vi, starti, endi]。

0 <= ui, vi <= n - 1。

ui != vi。

0 <= starti <= endi <= 1000000000。

输入: n = 4, edges = [[0,1,0,3],[1,3,7,8],[0,2,1,5],[2,3,4,7]]。

输出: 5。

解释:

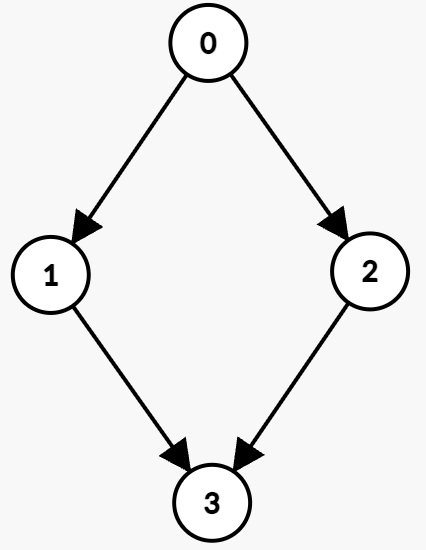
最佳路径为：

在节点 0 等待直到时间 t = 1，然后走边 (0 → 2)，该边在 1 到 5 的时间段内可用。你在 t = 2 到达节点 2。

在节点 2 等待直到时间 t = 4，然后走边 (2 → 3)，该边在 4 到 7 的时间段内可用。你在 t = 5 到达节点 3。

因此，到达节点 3 的最小时间是 5。

题目来自力扣3604。

分步骤过程描述

1. 图构建阶段：

   • 代码首先将输入的四元组边（edges[i] = [ui, vi, starti, endi]）转换为邻接表表示的图。每个节点对应一个列表，存储从其出发的边信息。每条边记录目标节点（to）、边可用的起始时间（start）和结束时间（end）。例如，对于输入示例，节点0有两条边：一条指向节点1（时间窗口[0,3]），另一条指向节点2（时间窗口[1,5]）。

2. 数据初始化：

   • 初始化一个距离数组dis，长度为节点数n，所有元素初始化为极大值（math.MaxInt），表示初始时从节点0到各节点的最短时间未知。例外是dis[0] = 0，因为起点时刻为0。
   • 创建一个最小堆（优先队列）h，用于按时间顺序处理节点。堆中存储pair结构，包含当前时间（d）和节点编号（x）。初始时将起点(d=0, x=0)加入堆。

3. 主循环（Dijkstra核心逻辑）：

   • 循环从堆中弹出时间最小的pair（即当前最早可处理的节点）。若弹出的时间d大于dis[x]（说明该节点已被更优路径更新），则直接跳过，避免重复计算。
   • 若当前节点x是终点n-1，立即返回d作为答案，因此时已找到最短时间。
   • 遍历节点x的所有出边。对于每条边：
     • 计算新时间：移动需满足边的时间窗口约束。首先，必须等待至边可用（若当前时间d小于边的起始时间start，则等待到start）；然后移动耗时1单位。因此，新时间newD = max(d, e.start) + 1。
     • 验证时间窗口：移动操作开始的时刻（即newD - 1）必须在边的结束时间end之前（即newD - 1 <= e.end）。否则边已失效，不可用。
     • 更新距离：若上述条件满足且newD小于目标节点y的当前最短时间dis[y]，则更新dis[y] = newD，并将(newD, y)加入堆，供后续处理。

4. 等待行为的隐式处理：

   • 算法通过max(d, e.start)自动处理节点等待：若当前时间早于边起始时间，则等待至start；否则立即移动。这模拟了题目中“留在当前节点不动”的选项，无需显式操作。

5. 终止条件：

   • 若堆为空仍未到达终点，返回-1，表示终点不可达。例如，若所有边的时间窗口过早结束或路径不连通，则会触发此情况。

时间复杂度与空间复杂度

• 时间复杂度：算法基于Dijkstra的优先队列实现。每个节点最多被处理一次（通过dis数组去重），但每条边可能触发一次堆操作（插入或更新）。堆操作（插入或弹出）复杂度为O(log N)，其中N为节点数。因此，总复杂度为 O((N + E) log N)，其中E为边数。
• 空间复杂度：主要空间消耗为：
  • 邻接表存储图：O(E)。
  • 距离数组dis：O(N)。
  • 优先队列堆：最坏情况下存储O(N)个节点。
  • 总空间复杂度为 O(N + E)。

此方案通过扩展Dijkstra算法，高效结合了时间窗口约束，适用于大规模图（N和E可达100,000）。

Go完整代码如下：

package main

import (
	"container/heap"
	"fmt"
	"math"
)

func minTime(n int, edges [][]int) int {
	type edge struct{ to, start, end int }
	g := make([][]edge, n)
	for _, e := range edges {
		x, y := e[0], e[1]
		g[x] = append(g[x], edge{y, e[2], e[3]})
	}

	dis := make([]int, n)
	for i := range dis {
		dis[i] = math.MaxInt
	}
	dis[0] = 0
	h := hp{{}}

	for len(h) > 0 {
		p := heap.Pop(&h).(pair)
		d := p.d
		x := p.x
		if d > dis[x] {
			continue
		}
		if x == n-1 {
			return d
		}
		for _, e := range g[x] {
			y := e.to
			newD := max(d, e.start) + 1
			if newD-1 <= e.end && newD < dis[y] {
				dis[y] = newD
				heap.Push(&h, pair{newD, y})
			}
		}
	}
	return -1
}

type pair struct{ d, x int }
type hp []pair

func (h hp) Len() int           { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].d < h[j].d }
func (h hp) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v any)        { *h = append(*h, v.(pair)) }
func (h *hp) Pop() (v any)      { a := *h; *h, v = a[:len(a)-1], a[len(a)-1]; return }

func main() {
	n := 4
	edges := [][]int{{0, 1, 0, 3}, {1, 3, 7, 8}, {0, 2, 1, 5}, {2, 3, 4, 7}}
	result := minTime(n, edges)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

import heapq
import math
from typing import List

def minTime(n: int, edges: List[List[int]]) -> int:
    # 构建图，每个元素是 (邻接节点, start, end)
    graph = [[] for _ in range(n)]
    for e in edges:
        x, y, start, end = e
        graph[x].append((y, start, end))
    
    # 初始化距离数组
    dist = [math.inf] * n
    dist[0] = 0
    
    # 优先队列，存储 (距离, 节点)
    pq = [(0, 0)]  # (当前时间, 节点)
    
    while pq:
        d, x = heapq.heappop(pq)
        
        # 如果当前距离不是最短距离，跳过
        if d > dist[x]:
            continue
        
        # 到达终点
        if x == n - 1:
            return int(d)
        
        # 遍历邻接边
        for y, start, end in graph[x]:
            # 计算新到达时间：必须至少等到 start 时刻
            new_d = max(d, start) + 1
            
            # 检查是否在有效时间内，且距离更短
            if new_d - 1 <= end and new_d < dist[y]:
                dist[y] = new_d
                heapq.heappush(pq, (new_d, y))
    
    return -1

# 测试用例
if __name__ == "__main__":
    n = 4
    edges = [[0, 1, 0, 3], [1, 3, 7, 8], [0, 2, 1, 5], [2, 3, 4, 7]]
    result = minTime(n, edges)
    print(result)  # 输出结果

C++完整代码如下：

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <algorithm>

using namespace std;

struct Edge {
    int to, start, end;
    Edge(int t, int s, int e) : to(t), start(s), end(e) {}
};

struct Node {
    int time, id;
    Node(int t, int i) : time(t), id(i) {}

    // 重载运算符，用于最小堆
    bool operator>(const Node& other) const {
        return time > other.time;
    }
};

int minTime(int n, vector<vector<int>>& edges) {
    // 构建图
    vector<vector<Edge>> graph(n);
    for (const auto& e : edges) {
        int x = e[0], y = e[1], start = e[2], end = e[3];
        graph[x].emplace_back(y, start, end);
    }

    // 初始化距离数组
    vector<int> dist(n, INT_MAX);
    dist[0] = 0;

    // 优先队列（最小堆）
    priority_queue<Node, vector<Node>, greater<Node>> pq;
    pq.emplace(0, 0);

    while (!pq.empty()) {
        Node curr = pq.top();
        pq.pop();

        int d = curr.time;
        int x = curr.id;

        // 如果当前距离不是最短距离，跳过
        if (d > dist[x]) {
            continue;
        }

        // 到达终点
        if (x == n - 1) {
            return d;
        }

        // 遍历邻接边
        for (const auto& e : graph[x]) {
            int y = e.to;
            int start = e.start;
            int end = e.end;

            // 计算新到达时间：必须至少等到 start 时刻
            int new_d = max(d, start) + 1;

            // 检查是否在有效时间内，且距离更短
            if (new_d - 1 <= end && new_d < dist[y]) {
                dist[y] = new_d;
                pq.emplace(new_d, y);
            }
        }
    }

    return -1;
}

int main() {
    int n = 4;
    vector<vector<int>> edges = {
        {0, 1, 0, 3},
        {1, 3, 7, 8},
        {0, 2, 1, 5},
        {2, 3, 4, 7}
    };

    int result = minTime(n, edges);
    cout << result << endl;

    return 0;
}