2025-12-13：十六进制和三十六进制转化。用go语言，给定一个整数 n，先求它的平方并把该值用大写字母的 16 进制表示（符号位按需处理，数位使用 0–9 与 A–F），再求它的立方并将该值用大写字母的 36 进制表示（数位使用 0–9 与 A–Z）。

最后将这两个进制字符串按顺序拼接，作为函数的返回结果。

1 <= n <= 1000。

输入：n = 13。

输出： “A91P1”。

解释：

n * n = 13 * 13 = 169。在十六进制中，它转换为 (10 * 16) + 9 = 169，对应于 “A9”。

n * n * n = 13 * 13 * 13 = 2197。在三十六进制中，它转换为 (1 * 362) + (25 * 36) + 1 = 2197，对应于 “1P1”。

连接两个结果得到 “A9” + “1P1” = “A91P1”。

题目来自力扣3602。

分步过程描述

1. 给定整数 n = 13
   计算它的平方：
   ( n^2 = 13 \times 13 = 169 )

2. 平方值转换为十六进制

   • 调用 toRadix(169, 16)
   • 169 除以 16 的商和余数依次是：
     • 169 ÷ 16 = 10 余 9
     • 10 ÷ 16 = 0 余 10
   • 余数映射到十六进制字符：9 → ‘9’，10 → ‘A’
   • 余数收集的顺序是从低位到高位（9, 10），即 “9A”，但最后要反转，所以得到 “A9”。

3. 计算立方
   ( n^3 = 13 \times 13 \times 13 = 2197 )

4. 立方值转换为三十六进制

   • 调用 toRadix(2197, 36)
   • 2197 除以 36 的步骤：
     • 2197 ÷ 36 = 61 余 1
       • 余数 1 → ‘1’
     • 61 ÷ 36 = 1 余 25
       • 余数 25 → ‘Z’？不对，要检查字母映射：
         余数 0–9 → ‘0’–‘9’，余数 10 → ‘A’，余数 11 → ‘B’，…，余数 25 → 10+15 = 第 16 个字母？ 10→A(0), 11→B(1), …, 25 是 10+15，所以余数 25 是 10(A)+15 = 第 16 个字母是 P。
         验证：余数 10 → ‘A’，11 → ‘B’，12 → ‘C’，…，25 → ‘A’ + 15 = ‘P’ ✅
     • 1 ÷ 36 = 0 余 1
       • 余数 1 → ‘1’
   • 从低位到高位余数为 1, 25, 1，反转后是 1, 25, 1 → 字符 ‘1’, ‘P’, ‘1’ → 字符串 “1P1”。

5. 拼接结果

   • 十六进制部分 “A9” + 三十六进制部分 “1P1” → “A91P1”

复杂度分析

假设 ( n ) 给定，平方和立方计算是 ( O(1) )。

• 进制转换时，循环次数取决于数字在相应进制下的位数，最坏情况出现在 ( n = 1000 )：
  • 平方最大是 ( 10^6 )，十六进制下约 5 位。
  • 立方最大是 ( 10^9 )，三十六进制下约 6 位。
  • 每次循环是常数时间操作。

时间复杂度：
每次转换的位数是 ( O(\log M) )，这里 M 是 ( n^2 ) 或 ( n^3 )。由于输入 n ≤ 1000，位数不超过常数范围，所以可视为 ( O(1) )。但通常按大 O 表示法，是 ( O(\log n) )。

空间复杂度：
主要是 strings.Builder 存储的字符串长度，以及反转时用的 []rune 临时空间。额外空间与结果字符串长度成线性，结果字符串长度是 ( O(\log n) )。

结论：

• 总时间复杂度：( O(\log n) )（但 n ≤ 1000 时可看作 ( O(1) )）
• 总额外空间复杂度：( O(\log n) )（存储转换结果所需空间）

Go完整代码如下：

package main

import (
	"fmt"
	"strings"
)

func concatHex36(n int) string {
	h := n * n
	ans := toRadix(h, 16)

	h = n * n * n
	ans += toRadix(h, 36)

	return ans
}

func toRadix(num, radix int) string {
	if num == 0 {
		return "0"
	}

	var builder strings.Builder
	for num > 0 {
		rem := num % radix
		var ch byte
		if rem < 10 {
			ch = byte('0' + rem)
		} else {
			ch = byte('A' + rem - 10)
		}
		builder.WriteByte(ch)
		num /= radix
	}

	// 反转字符串
	runes := []rune(builder.String())
	for i, j := 0, len(runes)-1; i < j; i, j = i+1, j-1 {
		runes[i], runes[j] = runes[j], runes[i]
	}

	return string(runes)
}

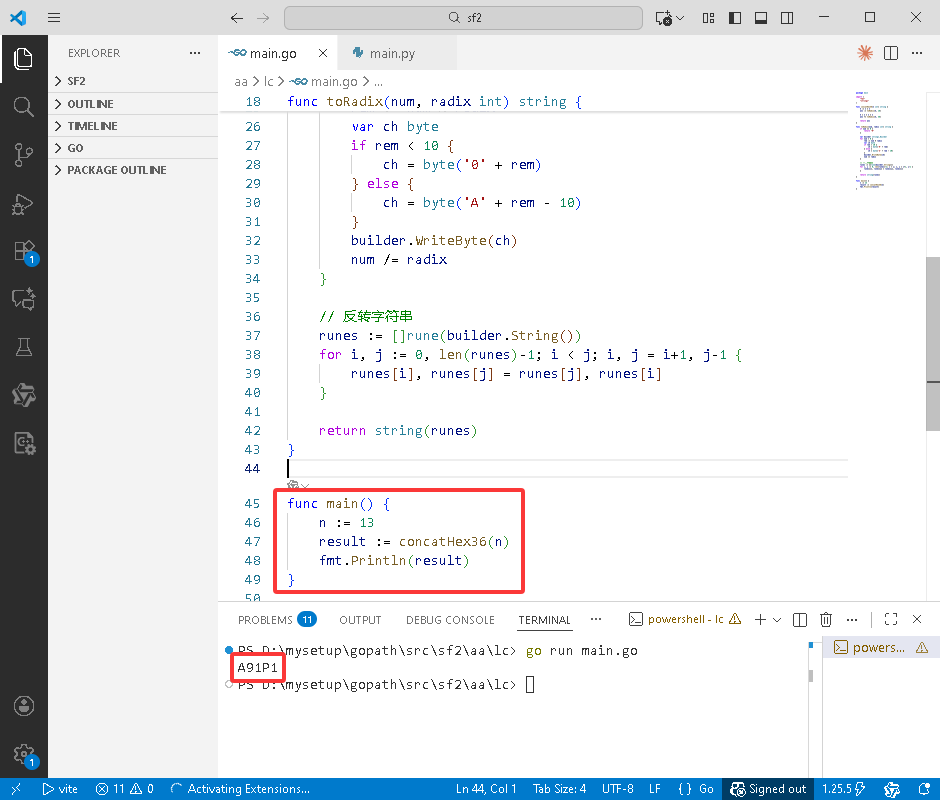
func main() {
	n := 13
	result := concatHex36(n)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

def to_radix(num: int, radix: int) -> str:
    """将十进制整数转换为指定进制的字符串表示"""
    if num == 0:
        return "0"
    
    digits = []
    while num > 0:
        rem = num % radix
        if rem < 10:
            digits.append(chr(ord('0') + rem))
        else:
            digits.append(chr(ord('A') + rem - 10))
        num //= radix
    
    return ''.join(reversed(digits))

def concat_hex36(n: int) -> str:
    """返回 n^2 的十六进制字符串与 n^3 的三十六进制字符串的拼接"""
    h = n * n
    ans = to_radix(h, 16)
    
    h = n * n * n
    ans += to_radix(h, 36)
    
    return ans

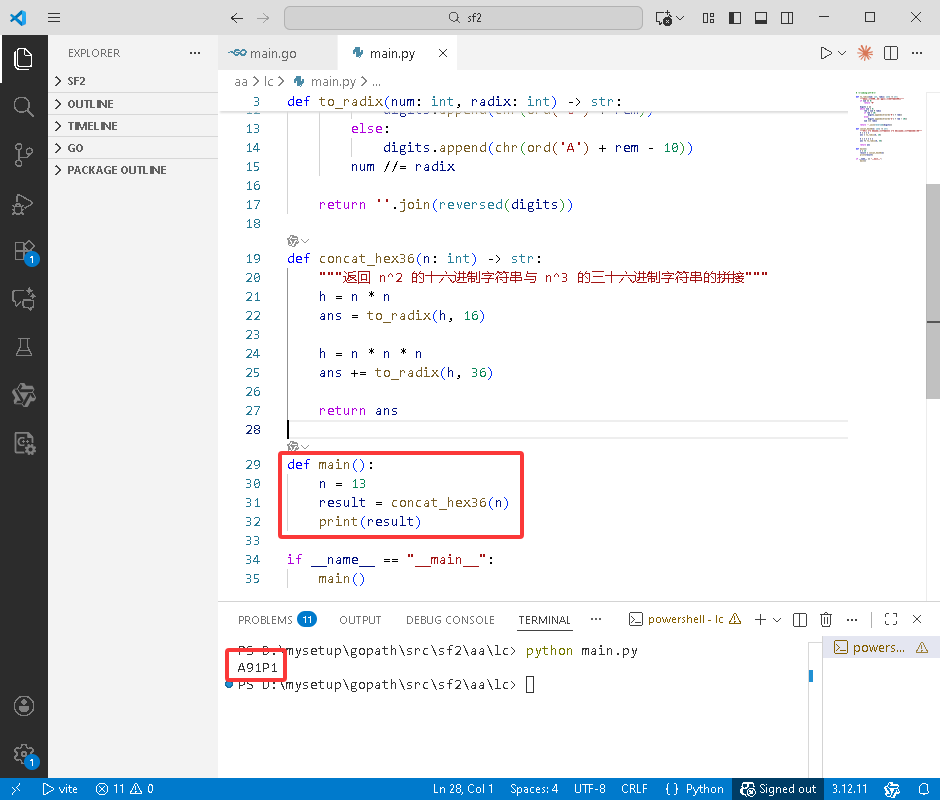
def main():
    n = 13
    result = concat_hex36(n)
    print(result)

if __name__ == "__main__":
    main()

C++完整代码如下：

#include <iostream>
#include <string>

std::string to_radix_no_reverse(int num, int radix) {
    if (num == 0) return "0";

    // 计算最大可能位数
    int temp = num;
    int digits = 0;
    while (temp > 0) {
        temp /= radix;
        digits++;
    }

    // 从最高位开始构建
    std::string result(digits, '\0');
    for (int i = digits - 1; i >= 0; --i) {
        int rem = num % radix;
        result[i] = (rem < 10) ? ('0' + rem) : ('A' + rem - 10);
        num /= radix;
    }

    return result;
}

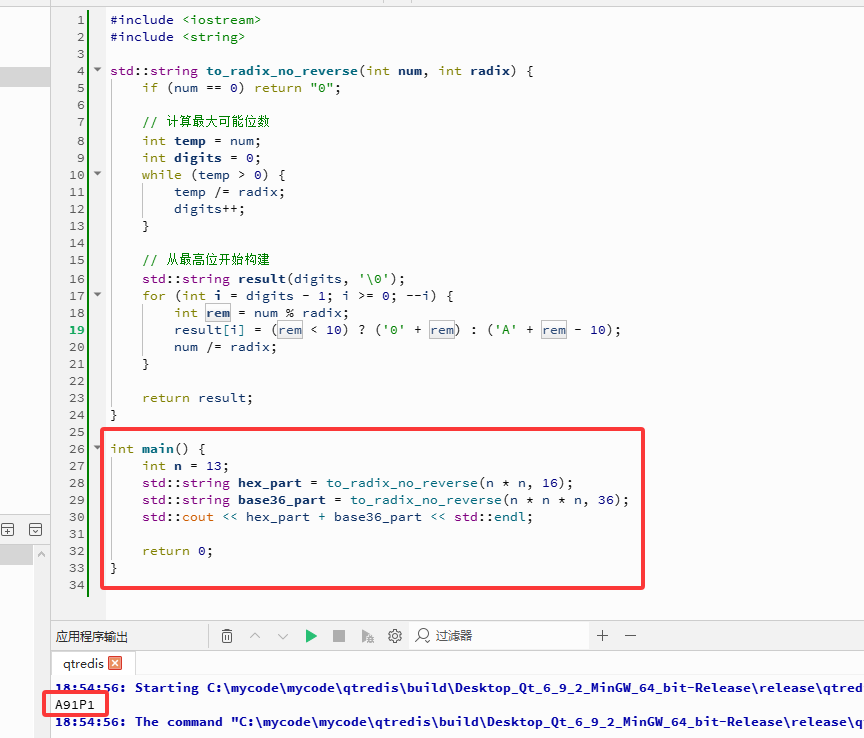
int main() {
    int n = 13;
    std::string hex_part = to_radix_no_reverse(n * n, 16);
    std::string base36_part = to_radix_no_reverse(n * n * n, 36);
    std::cout << hex_part + base36_part << std::endl;

    return 0;
}