2025-12-02：找到最大三角形面积。用go语言，给出一个大小为 n×2 的二维数组 coords，表示平面上 n 个点的坐标。任务是从这些点中任取三点构成三角形，并且要求该三角形至少有一条边与 x 轴或 y 轴平行。求所有满足条件的三角形中面积最大的那个的两倍（即 2A），若不存在符合条件且面积非零的三角形则返回 -1。

说明补充：

• 面积为零的不计入（即退化为直线的三角形不允许）。

• 可以用向量叉积或行列式来计算两倍面积：2A = |(x2−x1)(y3−y1) − (x3−x1)(y2−y1)|。

1 <= n == coords.length <= 100000。

1 <= coords[i][0], coords[i][1] <= 1000000。

所有 coords[i] 都是 唯一 的。

输入： coords = [[1,1],[1,2],[3,2],[3,3]]。

输出： 2。

解释：

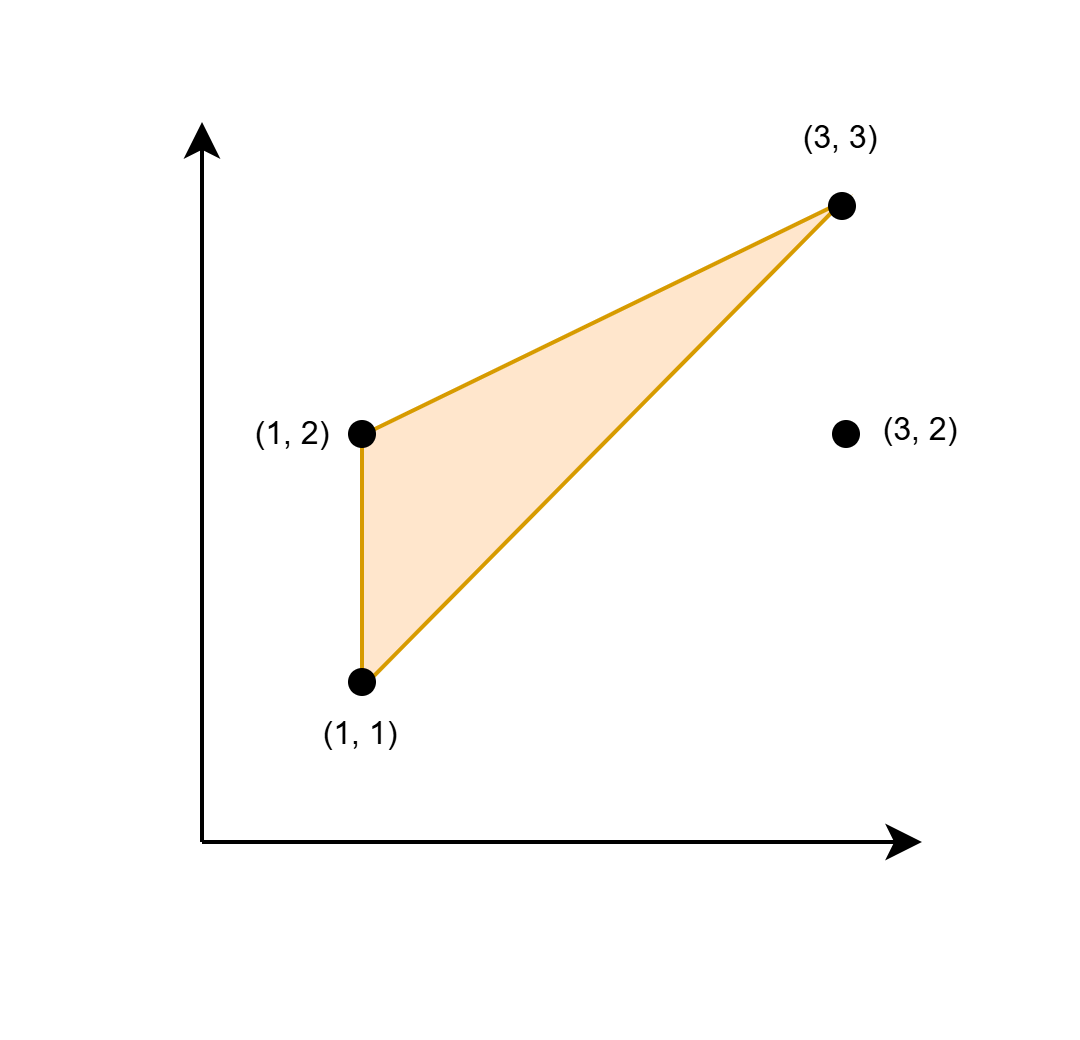
图中的三角形的底边为 1，高为 2。因此，它的面积为 1/2 * 底边 * 高 = 1。

题目来自力扣3588。

过程分步骤描述

1. 问题转换与关键洞察

   • 目标不是直接计算三角形面积 (A)，而是其两倍 (2A)。对于至少有一条边与坐标轴平行的三角形，(2A) 可直接由“底边长度 × 高度”得到（无需乘以 (1/2)）。例如：
     • 若一条边与 y轴平行（即x固定），则该边可作为高度（垂直方向），底边为水平方向的最大距离。
     • 若一条边与 x轴平行（即y固定），则该边可作为底边（水平方向），高度为垂直方向的最大距离。
   • 代码通过切换坐标轴统一处理两种情况：calc(0) 处理与y轴平行的边，calc(1) 处理与x轴平行的边。

2. 处理与y轴平行的边（calc(0)）

   • 坐标映射：遍历所有点，以原始x坐标作为分类依据，y坐标作为值。记录每个x对应的最小y（minY[x]）和最大y（maxY[x]），同时记录全局最小x（minX）和最大x（maxX）。
   • 计算高度和底边：对于每个x，高度 (h = \text{maxY}[x] - \text{minY}[x])（即该x轴上点的垂直跨度）。底边长度 (d = \max(\text{maxX} - x, x - \text{minX}))，表示从x到最左或最右点的水平最大距离。
   • 计算2A：(2A = h \times d)。此值对应以垂直线段为高度、水平距离为底边的三角形面积的两倍。

3. 处理与x轴平行的边（calc(1)）

   • 坐标切换：将点的y坐标视为x轴，x坐标视为y轴（即旋转坐标系）。此时，固定y值相当于原坐标系中固定x值，转化为与“y轴平行”的同类问题。
   • 重复步骤2的过程：计算每个y对应的水平跨度（高度）和垂直最大距离（底边），得到另一种方向下的 (2A)。

4. 结果合并与校验

   • 取 calc(0) 和 calc(1) 的最大值作为候选结果。若结果为0（表示所有三角形退化为直线或不存在），返回-1；否则返回该值。

时间复杂度和空间复杂度

• 时间复杂度：(O(n))，其中 (n) 是点的数量。
  • 每次 calc 调用需遍历所有点一次（构建映射）和第二次遍历映射键（计算最大2A），映射键数最多为 (n)（点坐标唯一）。
  • 两次调用 calc（分别对应j=0和j=1），总操作次数为 (2 \times O(n) = O(n))。
• 空间复杂度：(O(n))。
  • 主要开销是存储 minY 和 maxY 映射，最坏情况下（所有点x坐标互异）需 (O(n)) 空间。
  • 其他变量（如minX、maxX）为常数空间。

为什么此算法高效？

• 传统方法需枚举所有三点组合（(O(n^3))），但本题利用“与坐标轴平行”的约束，将问题简化为查找点集的边界信息，避免三重循环。
• 通过坐标轴切换，统一处理两种平行情况，确保覆盖所有可能的最大三角形。

此方案在 (n \leq 100000) 时能高效运行，符合题目要求。

Go完整代码如下：

package main

import (
	"fmt"
	"math"
)

func maxArea(coords [][]int) int64 {
	calc := func(j int) (res int) {
		minX, maxX := math.MaxInt, 0
		minY := map[int]int{}
		maxY := map[int]int{}
		for _, p := range coords {
			x, y := p[j], p[1-j]
			minX = min(minX, x)
			maxX = max(maxX, x)
			maxY[x] = max(maxY[x], y)
			mn, ok := minY[x]
			if !ok {
				minY[x] = y
			} else {
				minY[x] = min(mn, y)
			}
		}

		for x, y := range minY {
			res = max(res, (maxY[x]-y)*max(maxX-x, x-minX))
		}
		return
	}

	ans := max(calc(0), calc(1))
	if ans == 0 {
		ans = -1
	}
	return int64(ans)
}

func main() {
	coords := [][]int{{1, 1}, {1, 2}, {3, 2}, {3, 3}}
	result := maxArea(coords)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

from typing import List
import math

def max_area(coords: List[List[int]]) -> int:
    def calc(j: int) -> int:
        min_x, max_x = math.inf, 0
        min_y = {}
        max_y = {}
        
        for p in coords:
            x, y = p[j], p[1 - j]
            min_x = min(min_x, x)
            max_x = max(max_x, x)
            max_y[x] = max(max_y.get(x, y), y)
            min_y[x] = min(min_y.get(x, y), y)
        
        res = 0
        for x, y in min_y.items():
            width = max(max_x - x, x - min_x)
            height = max_y[x] - y
            res = max(res, height * width)
        return res
    
    ans = max(calc(0), calc(1))
    return -1 if ans == 0 else ans

# 测试示例
coords = [[1, 1], [1, 2], [3, 2], [3, 3]]
result = max_area(coords)
print(result)  # 输出结果

C++完整代码如下：

#include <iostream>
#include <vector>
#include <map>
#include <climits>
#include <algorithm>
using namespace std;

long long maxArea(vector<vector<int>>& coords) {
    auto calc = [&](int j) -> long long {
        int minX = INT_MAX, maxX = 0;
        map<int, int> minY;
        map<int, int> maxY;

        for (auto& p : coords) {
            int x = p[j];
            int y = p[1 - j];

            minX = min(minX, x);
            maxX = max(maxX, x);

            // 更新最大y值
            if (maxY.find(x) == maxY.end()) {
                maxY[x] = y;
            } else {
                maxY[x] = max(maxY[x], y);
            }

            // 更新最小y值
            if (minY.find(x) == minY.end()) {
                minY[x] = y;
            } else {
                minY[x] = min(minY[x], y);
            }
        }

        long long res = 0;
        for (auto& [x, y] : minY) {
            int width = max(maxX - x, x - minX);
            int height = maxY[x] - y;
            res = max(res, (long long)width * height);
        }
        return res;
    };

    long long ans = max(calc(0), calc(1));
    return (ans == 0) ? -1 : ans;
}

int main() {
    vector<vector<int>> coords = {{1, 1}, {1, 2}, {3, 2}, {3, 3}};
    long long result = maxArea(coords);
    cout << result << endl;  // 输出结果
    return 0;
}