2025-11-29:子序列首尾元素的最大乘积。用go语言,给你一个整数数组 nums 和一个正整数 m。你需要从 nums 中
【摘要】 2025-11-29:子序列首尾元素的最大乘积。用go语言,给你一个整数数组 nums 和一个正整数 m。你需要从 nums 中按原有相对顺序挑出恰好 m 个元素(可以丢弃其它元素),在所有这样的长度为 m 的筛选结果中,计算每个序列第一个元素与最后一个元素的乘积,并返回这些乘积中的最大值。1 <= nums.length <= 100000。-100000 <= nums[i] <= 10...
2025-11-29:子序列首尾元素的最大乘积。用go语言,给你一个整数数组 nums 和一个正整数 m。你需要从 nums 中按原有相对顺序挑出恰好 m 个元素(可以丢弃其它元素),在所有这样的长度为 m 的筛选结果中,计算每个序列第一个元素与最后一个元素的乘积,并返回这些乘积中的最大值。
1 <= nums.length <= 100000。
-100000 <= nums[i] <= 100000。
1 <= m <= nums.length。
输入: nums = [-1,-9,2,3,-2,-3,1], m = 1。
输出: 81。
解释:
子序列 [-9] 的首尾元素乘积最大:-9 * -9 = 81。因此,答案是 81。
题目来自力扣3584。
过程分步描述
-
初始化变量:
- 将答案变量
ans初始化为最小整数值(math.MinInt),用于记录遍历过程中找到的最大乘积。 - 初始化两个变量
mn和mx:mn(最小值跟踪器)初始化为最大整数值(math.MaxInt),用于记录当前可能作为子序列第一个元素的最小值。mx(最大值跟踪器)初始化为最小整数值(math.MinInt),用于记录当前可能作为子序列第一个元素的最大值。
- 这些初始化确保在首次比较时能被正确更新。
- 将答案变量
-
遍历数组,枚举子序列的最后一个元素位置:
- 循环变量
i从索引m-1开始,直到数组末尾(len(nums)-1)。这是因为子序列长度必须为m,最后一个元素的索引至少为m-1(索引从0开始)。 - 对于每个可能的最后一个元素位置
i:
a. 确定当前子序列第一个元素的候选范围:- 对于固定的最后一个元素索引
i,第一个元素的索引j必须满足j <= i - m + 1。这是为了确保在j和i之间有足够的位置(至少m-2个索引)来挑选中间元素,形成长度为m的子序列。
b. 更新第一个元素候选值的最小值mn和最大值mx: - 获取当前第一个元素候选值
y = nums[i - m + 1](即当前候选范围的最右端索引对应的元素)。 - 更新
mn = min(mn, y),使mn始终记录从索引0到当前i - m + 1的所有可能第一个元素的最小值。 - 更新
mx = max(mx, y),使mx始终记录同一范围内的最大值。 - 例如,当
i增大时,mn和mx会累积覆盖更多候选元素,动态维护全局最小和最大值。
c. 计算当前子序列的首尾乘积候选值: - 获取当前最后一个元素的值
x = nums[i]。 - 计算两个关键乘积:
x * mn:最后一个元素与最小可能第一个元素的乘积。x * mx:最后一个元素与最大可能第一个元素的乘积。
- 由于数组元素可能为负数,同时考虑最小值和最大值可以覆盖乘积最大化的场景(例如,两个负数相乘可能得正且很大)。
d. 更新全局最大乘积ans: - 将
ans设置为当前ans、x * mn和x * mx中的最大值。 - 这确保在遍历过程中始终捕获所有可能子序列的首尾乘积最大值。
- 对于固定的最后一个元素索引
- 循环变量
-
返回结果:
- 循环结束后,将
ans转换为int64类型并返回。如果没有任何满足条件的子序列(理论上不会发生,因为m >= 1且数组非空),ans可能保持初始值,但题目保证有解。
- 循环结束后,将
时间和空间复杂度分析
- 时间复杂度:
O(n),其中n是数组nums的长度。代码通过单次遍历数组(从m-1到n-1),每个元素处理一次,操作均为常数时间(比较和算术运算)。枚举最后一个元素时,通过维护mn和mx避免了内部循环,高效覆盖所有可能第一个元素。 - 额外空间复杂度:
O(1)。算法只使用了固定数量的整数变量(如ans、mn、mx、循环索引等),不随输入规模n或m变化而占用额外空间。
关键点说明
- 有效性:代码利用动态维护极值的方法,避免了显式检查所有
O(n^2)可能的子序列组合,显著优化了性能。对于每个最后一个元素,直接使用累积的mn/mx确定最佳第一个元素,无需嵌套循环。 - 处理负数:通过同时跟踪最小值和最大值,确保在元素含负数时也能正确计算最大乘积(例如,负数乘以负数可能得正)。
- 示例验证:以输入
nums = [-1, -9, 2, 3, -2, -3, 1],m = 1为例,当m=1时,子序列仅含一个元素,首尾相同。代码遍历每个元素,计算其平方(即x * x),并通过维护mn/mx捕获最大值(-9)^2 = 81,与题目输出一致。
此方法高效且简洁,适用于大规模数组约束(n <= 100000)。
Go完整代码如下:
package main
import (
"fmt"
"math"
)
func maximumProduct(nums []int, m int) int64 {
ans := math.MinInt
mn, mx := math.MaxInt, math.MinInt
for i := m - 1; i < len(nums); i++ {
// 维护左边 [0,i-m+1] 中的最小值和最大值
y := nums[i-m+1]
mn = min(mn, y)
mx = max(mx, y)
// 枚举右
x := nums[i]
ans = max(ans, x*mn, x*mx)
}
return int64(ans)
}
func main() {
nums := []int{-1, -9, 2, 3, -2, -3, 1}
m := 1
result := maximumProduct(nums, m)
fmt.Println(result)
}
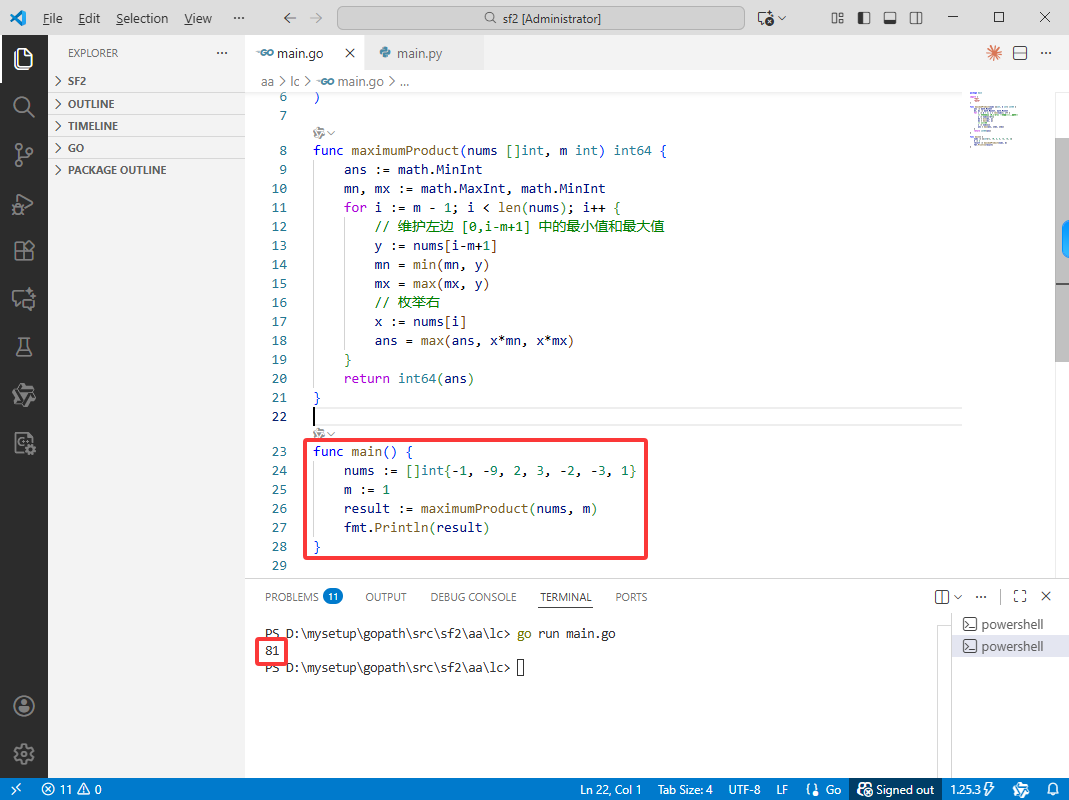
Python完整代码如下:
# -*-coding:utf-8-*-
def maximumProduct(nums, m):
if not nums or m <= 0 or m > len(nums):
return float('-inf')
max_product = float('-inf')
min_val = float('inf')
max_val = float('-inf')
for i in range(m - 1, len(nums)):
# 更新左侧窗口的最小值和最大值
left_val = nums[i - m + 1]
min_val = min(min_val, left_val)
max_val = max(max_val, left_val)
# 计算当前窗口右端点与最小/最大值的乘积
right_val = nums[i]
current_max = max(right_val * min_val, right_val * max_val)
max_product = max(max_product, current_max)
return max_product
# 测试
if __name__ == "__main__":
test_cases = [
([-1, -9, 2, 3, -2, -3, 1], 1),
]
for nums, m in test_cases:
result = maximumProduct(nums, m)
print(f"nums: {nums}, m: {m} -> result: {result}")
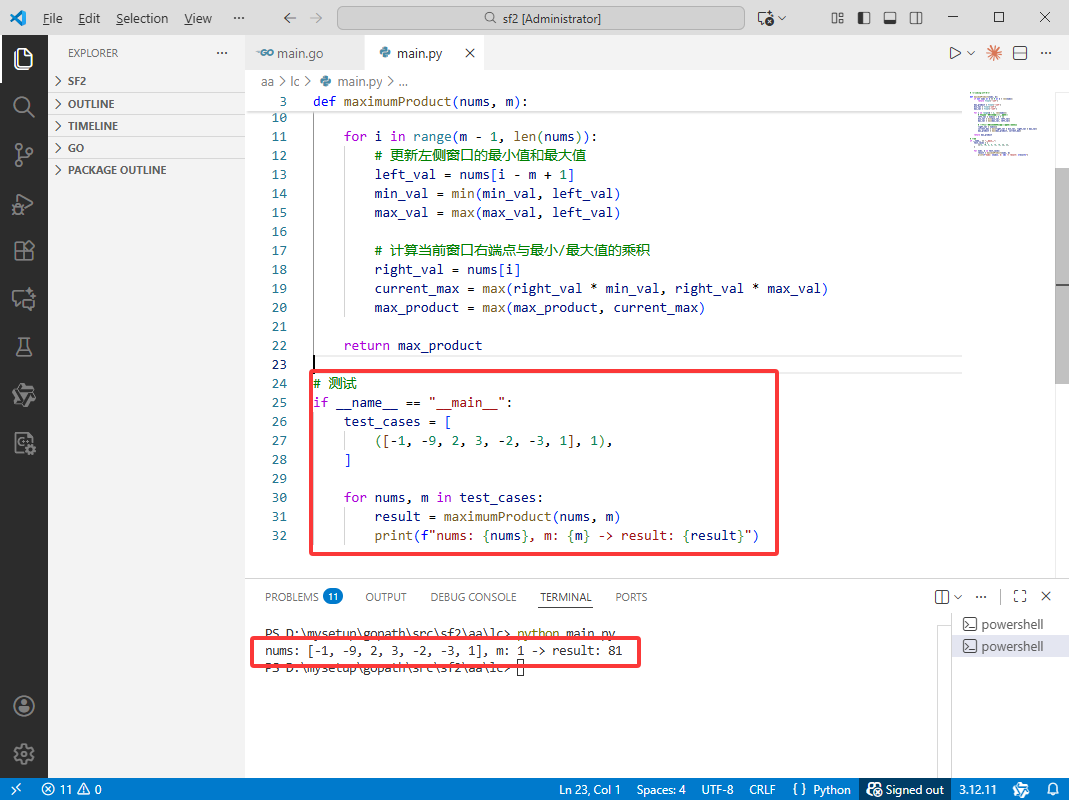
C++完整代码如下:
#include <iostream>
#include <vector>
#include <climits>
#include <algorithm>
using namespace std;
long long maximumProduct(vector<int>& nums, int m) {
long long ans = LLONG_MIN;
int mn = INT_MAX, mx = INT_MIN;
for (int i = m - 1; i < nums.size(); i++) {
// 维护左边 [0,i-m+1] 中的最小值和最大值
int y = nums[i - m + 1];
mn = min(mn, y);
mx = max(mx, y);
// 枚举右
int x = nums[i];
ans = max({ans, (long long)x * mn, (long long)x * mx});
}
return ans;
}
int main() {
vector<int> nums = {-1, -9, 2, 3, -2, -3, 1};
int m = 1;
long long result = maximumProduct(nums, m);
cout << result << endl;
return 0;
}
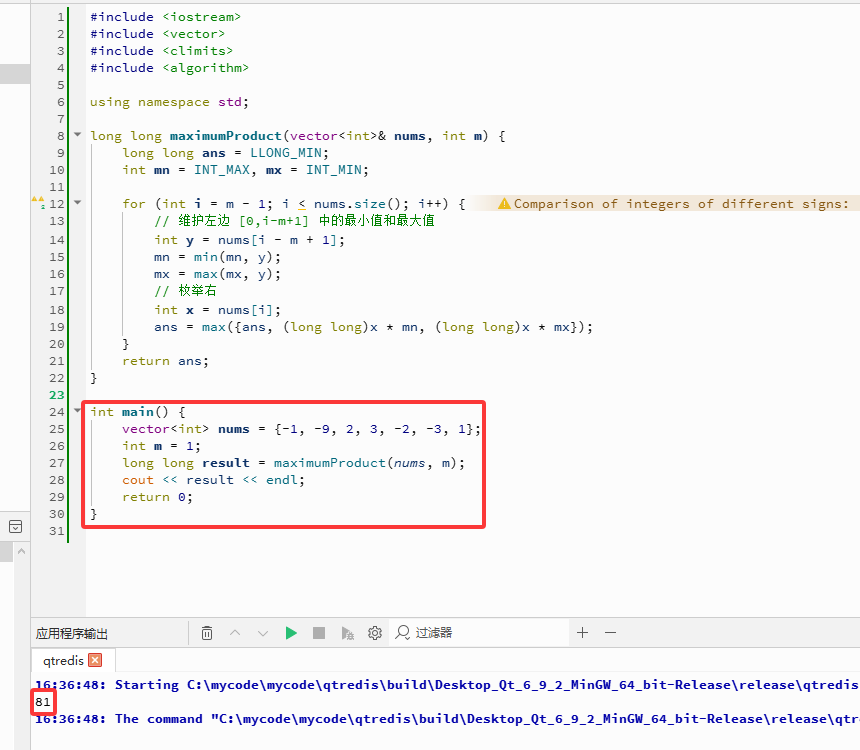
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)