2025-11-28：统计特殊三元组。用go语言，给定一个整数数组 nums。我们把满足 i<j<k（索引从 0 开始）且 nums[i] 和 nums[k] 都等于 nums[j] 的两倍的三个不同索引 (i, j, k) 称为“一组特殊三元组”。要求计算数组中所有这样的三元组数量，并将结果对 1000000007 取模后返回。

3 <= n == nums.length <= 100000。

0 <= nums[i] <= 100000。

输入： nums = [6,3,6]。

输出： 1。

解释：

唯一的特殊三元组是 (i, j, k) = (0, 1, 2)，其中：

nums[0] = 6, nums[1] = 3, nums[2] = 6

nums[0] = nums[1] * 2 = 3 * 2 = 6

nums[2] = nums[1] * 2 = 3 * 2 = 6

题目来自力扣3583。

过程分步说明

1. 初始化阶段
   代码使用了三个映射（map）来动态跟踪计数：

   • cnt1：记录每个数字作为三元组中第一个元素 nums[i] 出现的次数。键是数字本身，值是该数字在遍历过程中作为 nums[i] 的累计次数。
   • cnt12：记录每个数字作为中间值 nums[j] 时，当前已存在的有效 (i, j) 对数量。具体来说，对于给定的 nums[j]，cnt12[nums[j]] 表示之前已遇到多少对 (i, j) 满足 nums[i] = 2 * nums[j] 且 i < j。
   • cnt123：直接统计完整三元组 (i, j, k) 的数量。初始值为 0，最终结果需对 1_000_000_007 取模。

2. 遍历数组并动态更新计数
   代码从左到右遍历数组 nums，将每个元素 x 依次视为三元组中的潜在 k、j 或 i：

   • 步骤一：检查 x 作为 nums[k] 的可能性
     如果 x 是偶数（即 x % 2 == 0），则计算 x / 2 作为候选的 nums[j] 值。此时，若 cnt12 中已存在键 x/2，说明之前已记录过满足 nums[i] = 2 * nums[j] 的 (i, j) 对，且这些对的 nums[j] 正好是 x/2。当前 x 作为 nums[k] 可与这些 (i, j) 组合成完整三元组，因此将 cnt12[x/2] 的值累加到 cnt123 中。
   • 步骤二：更新 x 作为 nums[j] 的计数
     接下来，将 x 视为 nums[j]。需要找到所有满足 nums[i] = 2 * x 且 i < j 的 nums[i]。这些 nums[i] 的数量已记录在 cnt1[2*x] 中（即之前遍历时作为 i 出现的次数）。因此，将 cnt1[2*x] 的值加到 cnt12[x] 中，表示新增了 cnt1[2*x] 个有效的 (i, j) 对。
   • 步骤三：更新 x 作为 nums[i] 的计数
     最后，将 x 视为 nums[i]，简单增加 cnt1[x] 的计数，为后续 j 或 k 的匹配做准备。

3. 最终处理
   遍历完成后，cnt123 即为所有满足条件的三元组总数。返回 cnt123 % 1_000_000_007 以确保结果在模数范围内。

复杂度分析

• 总的时间复杂度：O(n)，其中 n 是数组长度。代码仅对数组进行一次线性遍历，每个元素处理过程中对映射的查询、插入和更新操作均摊时间复杂度为 O(1)（基于哈希映射实现）。
• 总的额外空间复杂度：O(n)。主要来自三个映射 cnt1、cnt12 和 cnt123 的存储。在最坏情况下，映射中的键数量与数组长度 n 成正比（例如所有元素互异时），因此空间复杂度为线性。

补充说明

• 算法的关键洞察：通过单次遍历和巧妙的计数映射，避免了暴力枚举所有三元组（否则复杂度为 O(n³)），实现了高效统计。这种方法类似于动态规划中“用空间换时间”的策略，逐步构建子问题的解。
• 与其他三元组问题的区别：不同于搜索和排序类三元组问题（如三数之和），本题专注于特定算术关系的计数，且数组元素无需排序。

Go完整代码如下：

package main

import (
	"fmt"
)

func specialTriplets(nums []int) (cnt123 int) {
	const mod = 1_000_000_007
	cnt1 := map[int]int{}
	cnt12 := map[int]int{}
	for _, x := range nums {
		if x%2 == 0 {
			cnt123 += cnt12[x/2] // 把 x 当作 nums[k]
		}
		cnt12[x] += cnt1[x*2] // 把 x 当作 nums[j]
		cnt1[x]++             // 把 x 当作 nums[i]
	}
	return cnt123 % mod
}

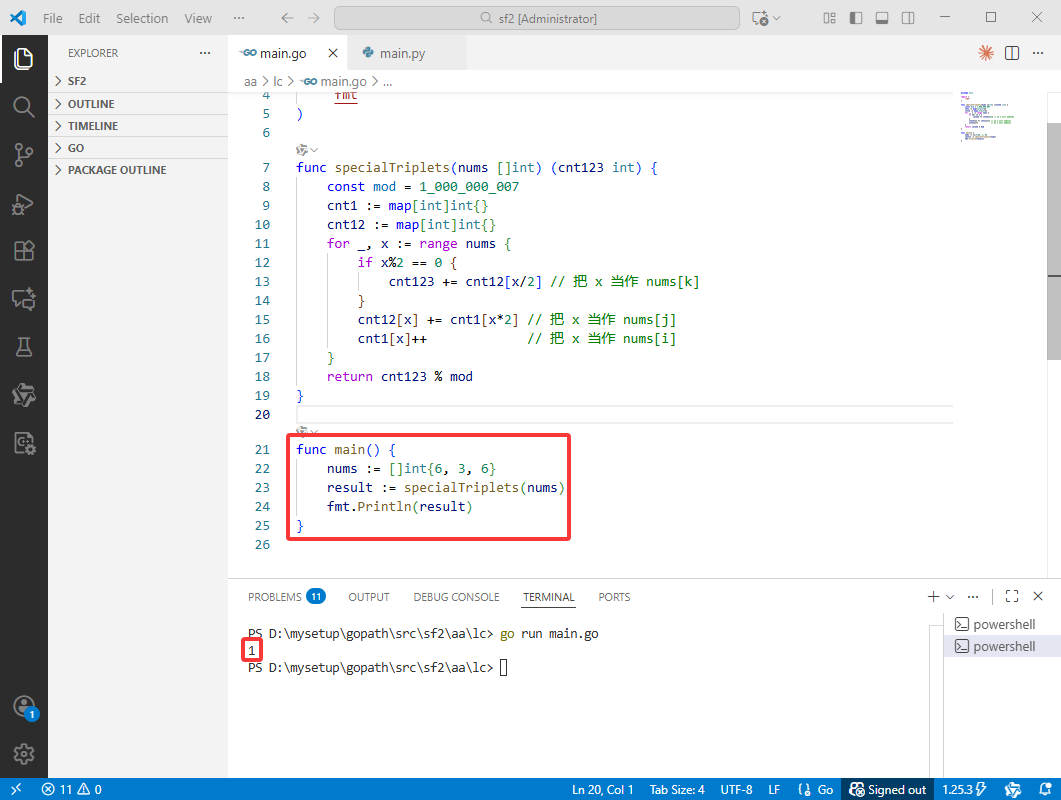
func main() {
	nums := []int{6, 3, 6}
	result := specialTriplets(nums)
	fmt.Println(result)
}

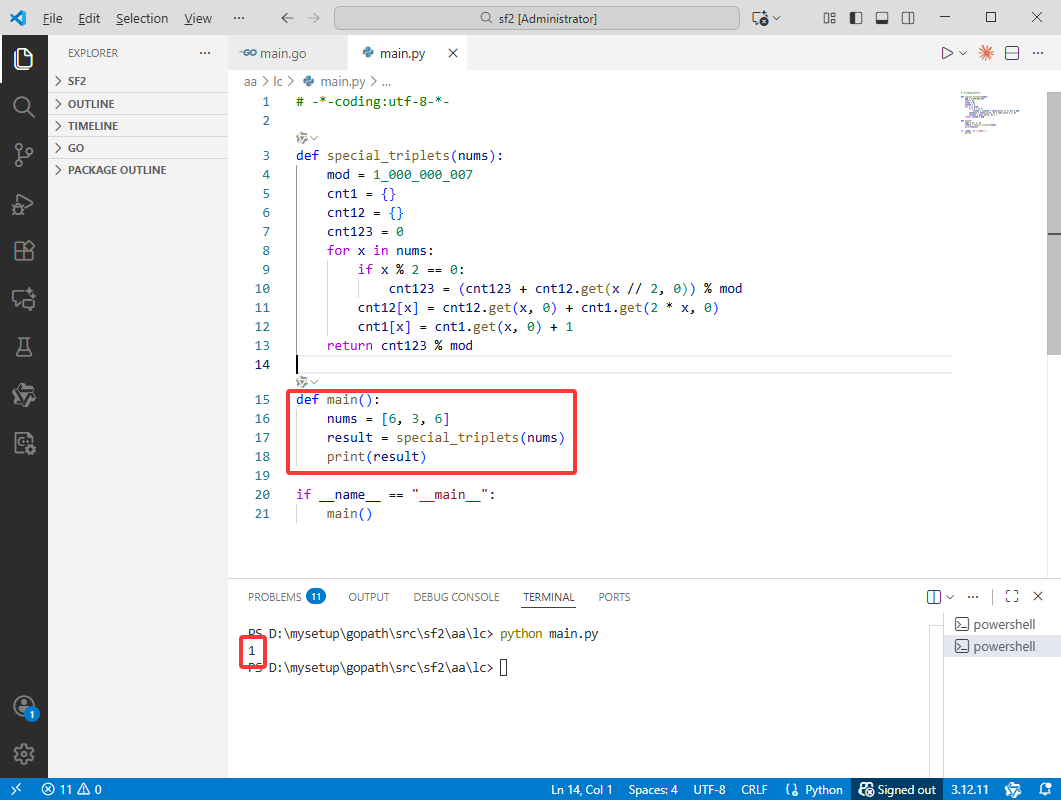
Python完整代码如下：

# -*-coding:utf-8-*-

def special_triplets(nums):
    mod = 1_000_000_007
    cnt1 = {}
    cnt12 = {}
    cnt123 = 0
    for x in nums:
        if x % 2 == 0:
            cnt123 = (cnt123 + cnt12.get(x // 2, 0)) % mod
        cnt12[x] = cnt12.get(x, 0) + cnt1.get(2 * x, 0)
        cnt1[x] = cnt1.get(x, 0) + 1
    return cnt123 % mod

def main():
    nums = [6, 3, 6]
    result = special_triplets(nums)
    print(result)

if __name__ == "__main__":
    main()

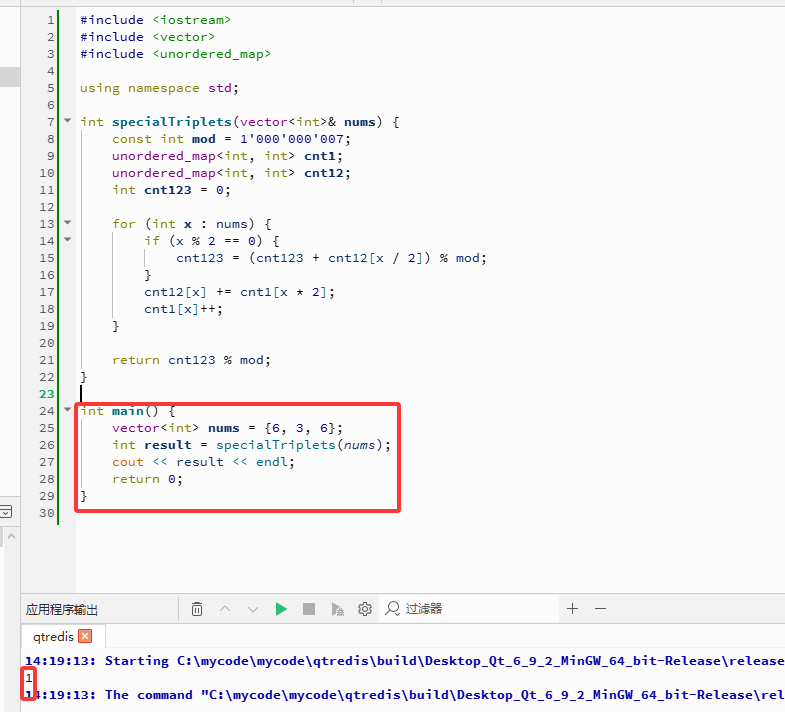
C++完整代码如下：

#include <iostream>
#include <vector>
#include <unordered_map>

using namespace std;

int specialTriplets(vector<int>& nums) {
    const int mod = 1'000'000'007;
    unordered_map<int, int> cnt1;
    unordered_map<int, int> cnt12;
    int cnt123 = 0;

    for (int x : nums) {
        if (x % 2 == 0) {
            cnt123 = (cnt123 + cnt12[x / 2]) % mod;
        }
        cnt12[x] += cnt1[x * 2];
        cnt1[x]++;
    }

    return cnt123 % mod;
}

int main() {
    vector<int> nums = {6, 3, 6};
    int result = specialTriplets(nums);
    cout << result << endl;
    return 0;
}