2025-11-23：数组元素相等转换。用go语言，给出一个长度为 n 的数组 nums，元素仅为 1 或 -1，和一个非负整数 k。

允许你执行不超过 k 次以下变换：选定一个索引 i（0 ≤ i < n−1），把位置 i 和 i+1 的两个数同时取相反数（即把它们的符号都反过来）。

同一个索引可以在不同操作中重复选择。判断是否存在一种不超过 k 步的操作序列，使得操作结束后数组中的所有元素都相同。

如果存在返回 true，否则返回 false。

<= n == nums.length <= 100000。

nums[i] 的值为 -1 或 1。

1 <= k <= n。

输入： nums = [1,-1,1,-1,1], k = 3。

输出： true。

解释：

我们可以通过以下两次操作使数组的所有元素相等：

选择下标 i = 1，将 nums[1] 和 nums[2] 同时乘以 -1。此时 nums = [1,1,-1,-1,1]。

选择下标 i = 2，将 nums[2] 和 nums[3] 同时乘以 -1。此时 nums = [1,1,1,1,1]。

题目来自力扣3576。

🔄 分步骤详细过程

1. 双目标检查

   • 算法首先明确最终的目标：数组中的所有元素必须全部是 1 或者全部是 -1。因此，它会分别针对这两种情况（target = 1 和 target = -1）进行独立的检查。
   • 只要其中任意一种情况能够在给定的操作次数 k 内实现，函数就会返回 true。这是一种常见的解题思路，通过枚举有限的可能结果来简化问题。

2. 贪心遍历与符号传播

   • 对于每一种目标值，算法采用一次从左到右的线性遍历。这个过程模拟了操作对数组元素符号的累积影响。
   • 在遍历过程中，算法维护两个关键状态：
     • left：剩余的可执行操作次数，初始值为 k。
     • mul：一个乘数因子（其值为 1 或 -1），用于表示由于之前位置的操作对当前正在检查的元素造成的累积符号翻转效应。初始值为 1，表示没有累积影响。

3. 处理每个元素

   • 对于数组中的每一个元素 nums[i]，算法计算其当前的有效值 nums[i] * mul。这个有效值反映了在考虑了之前所有操作的影响后，该元素当前“表现”出的符号。
   • 情况一：有效值等于目标值
     • 如果 nums[i] * mul 等于目标值，说明当前位置的元素符号已经是正确的，不需要执行操作。
     • 此时，将 mul 重置为 1。这意味着之前的操作链影响到此结束，下一个元素 nums[i+1] 的符号不会被本次遍历中之前的操作所影响。
   • 情况二：有效值不等于目标值
     • 如果 nums[i] * mul 不等于目标值，说明需要执行一次操作来翻转 nums[i] 和 nums[i+1] 的符号。
     • 首先检查是否满足执行操作的条件：① 剩余操作次数 left 大于 0；② 当前索引 i 不是数组的最后一个元素（因为操作需要同时改变 i 和 i+1 位置）。
     • 如果条件不满足，则说明无法使当前元素匹配目标，本次检查（对于当前目标值）失败。
     • 如果条件满足，则执行以下动作：
       • 剩余操作次数 left 减少 1。
       • 将乘数 mul 设置为 -1。这个操作非常关键：它意味着由于在位置 i 执行了翻转，下一个元素 nums[i+1] 的符号将会被改变。因此，在检查下一个位置时，需要通过乘以 -1 来“补偿”这次操作产生的影响。这个机制模拟了操作效应沿着数组向后传播的过程。

4. 最终判断

   • 如果遍历完所有元素，都没有因为无法匹配而提前返回，则说明可以在 k 次操作内使所有元素变为当前检查的目标值，返回 true。
   • 如果对于两个目标值（1 和 -1）的检查都失败了，则函数返回 false。

⏱️ 复杂度分析

• 总的时间复杂度：算法对数组进行了常数次（2次）完整的遍历。每次遍历的时间复杂度是 O(n)，其中 n 是数组 nums 的长度。因此，总的时间复杂度是 O(n)。
• 总的额外空间复杂度：算法只使用了固定数量的额外变量（如 left, mul, 循环变量 i 等），这些空间开销不随输入数组的大小 n 而变化。因此，总的额外空间复杂度是 O(1)。

Go完整代码如下：

package main

import (
	"fmt"
)

func canMakeEqual(nums []int, k int) bool {
	check := func(target int) bool {
		left := k
		mul := 1
		for i, x := range nums {
			if x*mul == target {
				mul = 1 // 不操作，下一个数不用乘 -1
				continue
			}
			if left == 0 || i == len(nums)-1 {
				return false
			}
			left--
			mul = -1 // 操作，下一个数要乘 -1
		}
		return true
	}
	return check(-1) || check(1)
}

func main() {
	nums := []int{1, -1, 1, -1, 1}
	k := 3
	result := canMakeEqual(nums, k)
	fmt.Println(result)
}

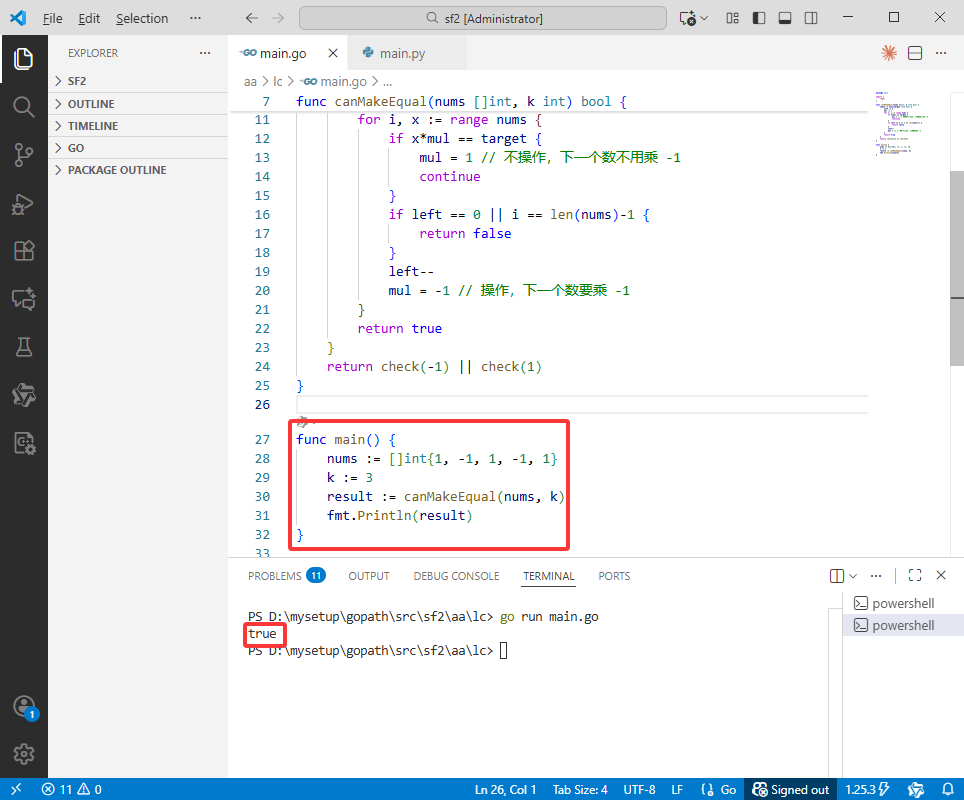
Python完整代码如下：

# -*-coding:utf-8-*-

def canMakeEqual(nums, k):
    def check(target):
        left = k
        mul = 1
        for i, x in enumerate(nums):
            if x * mul == target:
                mul = 1  # 不操作，下一个数不用乘 -1
                continue
            if left == 0 or i == len(nums) - 1:
                return False
            left -= 1
            mul = -1  # 操作，下一个数要乘 -1
        return True
    
    return check(-1) or check(1)

# 测试示例
if __name__ == "__main__":
    nums = [1, -1, 1, -1, 1]
    k = 3
    result = canMakeEqual(nums, k)
    print(result)  # 输出结果

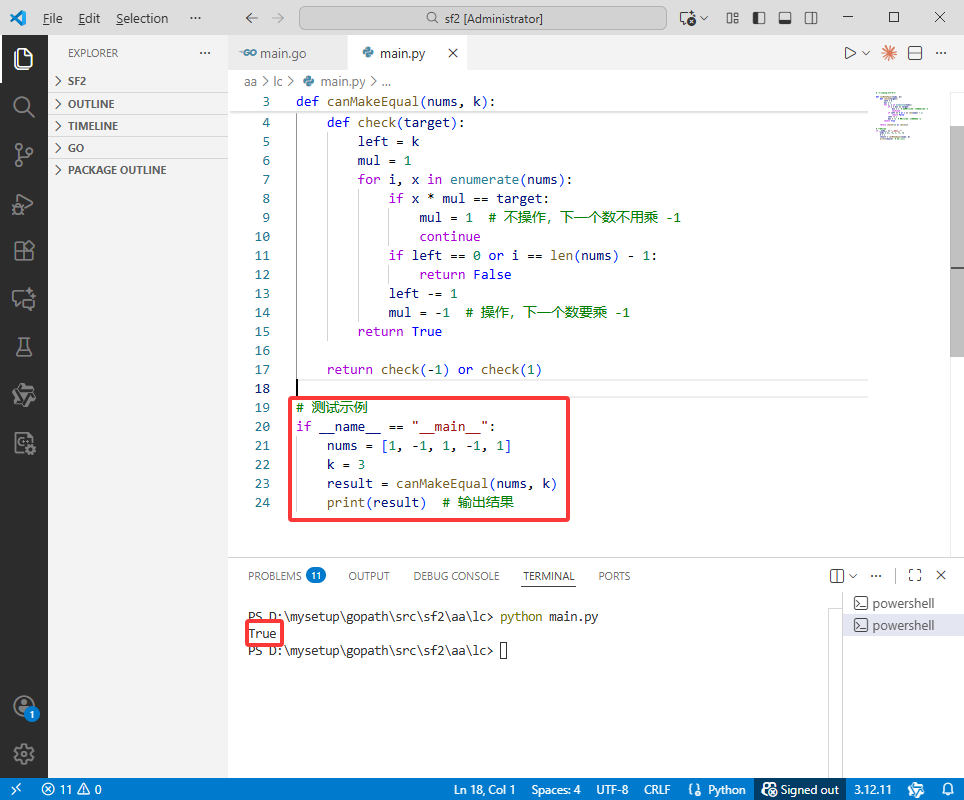
C++完整代码如下：

#include <iostream>
#include <vector>
using namespace std;

bool canMakeEqual(vector<int>& nums, int k) {
    auto check = [&](int target) -> bool {
        int left = k;
        int mul = 1;
        for (int i = 0; i < nums.size(); i++) {
            int x = nums[i];
            if (x * mul == target) {
                mul = 1; // 不操作，下一个数不用乘 -1
                continue;
            }
            if (left == 0 || i == nums.size() - 1) {
                return false;
            }
            left--;
            mul = -1; // 操作，下一个数要乘 -1
        }
        return true;
    };

    return check(-1) || check(1);
}

int main() {
    vector<int> nums = {1, -1, 1, -1, 1};
    int k = 3;
    bool result = canMakeEqual(nums, k);
    cout << boolalpha << result << endl; // 输出结果
    return 0;
}