2025-11-13：折扣价交易股票的最大利润。用go语言，公司有 n 名员工，编号从 1 到 n，编号 1 为 CEO。

present[i] 是第 i 位员工今天买入该员工股票所需的价格；future[i] 是明天卖出该员工股票能得到的期望价格（两个数组长度均为 n，索引从 1 开始）。

hierarchy 给出直接汇报关系：每个元素为一对 [u, v]，表示 u 是 v 的直接上司。

预算 budget 是可用于买入股票的初始资金（只能用这笔钱付款，不能先买后卖再用收益继续买）。

折扣规则：如果某位员工的直接上司也购买了自己的股票，那么该下属在今天买入时价格变为 floor(present[v] / 2)。

每只股票最多买一次。购买后可在明天以对应的 future 价格卖出，单只股票的净收益为 future[i]
减去实际支付的买入价（若为负则可选择不买）。

目标：在不超过初始预算的前提下，选择一组买入决策（同时决定哪些上司也买以触发折扣），使得所有选中股票在明天卖出后获得的总利润最大，并返回该最大利润值。

1 <= n <= 160。

present.length, future.length == n。

1 <= present[i], future[i] <= 50。

hierarchy.length == n - 1。

hierarchy[i] == [ui, vi]。

1 <= ui, vi <= n。

ui != vi。

1 <= budget <= 160。

没有重复的边。

员工 1 是所有员工的直接或间接上司。

输入的图 hierarchy 保证 无环 。

输入： n = 3, present = [4,6,8], future = [7,9,11], hierarchy = [[1,2],[1,3]], budget = 10。

输出： 10。

解释：

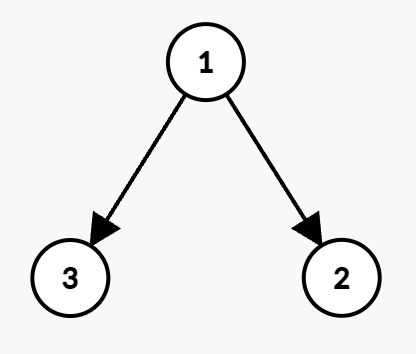
员工 1 以价格 4 购买股票，获得利润 7 - 4 = 3。

员工 3 可获得折扣价 floor(8 / 2) = 4，获得利润 11 - 4 = 7。

员工 1 和员工 3 的总购买成本为 4 + 4 = 8 <= budget，因此最大总利润为 3 + 7 = 10。

题目来自力扣3562。

过程描述

1. 构建员工树结构：

   • 根据输入的hierarchy（直接汇报关系），构建一个树形结构的邻接表g。每个节点代表一名员工，编号从0开始（对应原始编号1到n），其中节点0是CEO（根节点）。每个节点x的邻接表g[x]存储其所有直接下属（子节点）的编号。由于输入保证无环且员工1是所有员工的直接或间接上司，因此构建的树是以0为根的有根树。

2. 递归DFS遍历与状态定义：

   • 定义一个递归函数dfs(x)，用于处理以节点x为根的子树。该函数返回一个包含两个数组的结构[2][]int，每个数组长度为budget + 1：
     • 第一个数组（索引0）表示当x的直接上司不购买股票时，以x为根的子树在不同预算（0到budget）下能获得的最大利润。
     • 第二个数组（索引1）表示当x的直接上司购买股票时，对应子树在不同预算下的最大利润。
   • 初始时，所有利润值被设置为一个极小的负数（math.MinInt / 2），表示不可行状态，但预算为0时利润为0。

3. 合并子节点利润（子树合并）：

   • 对于当前节点x，遍历其每个直接下属（子节点）y：
     • 递归调用dfs(y)，获取子节点y的利润数组fy。fy[0]和fy[1]分别对应y的上司（即x）不买或买股票时y子树的利润。
     • 将每个子节点y的利润合并到x的临时状态数组subF中。合并过程类似分组背包问题：
       • 对于每个可能的预算j（从0到budget），以及分配给子节点y的预算jy（从0到j），计算将jy预算用于y子树所能获得的利润。如果fy[k][jy]为负（表示亏损），则跳过以优化效率。
       • 通过动态规划更新subF[k][j]（其中k表示x的上司状态），取subF[k][j - jy] + fy[k][jy]的最大值，即分配jy预算给y子树后，剩余预算用于其他子树的利润之和。

4. 处理当前节点x的购买决策：

   • 合并所有子节点利润后，得到subF数组，表示x的子树（不包括x本身）的利润。接下来计算x自身的购买决策：
     • 情况1：不购买x的股票：
       • 利润直接继承自subF[0]（因为x不买，其下属无法获得折扣，故使用subF[0]，对应下属的上司不买状态）。
     • 情况2：购买x的股票：
       • 实际成本cost取决于x的直接上司是否购买（即折扣规则）：
         • 如果上司购买（k = 1），成本为floor(present[x] / 2)（即present[x] / 2的整数除）。
         • 如果上司不购买（k = 0），成本为全价present[x]。
       • 利润计算公式为future[x] - cost（卖出价减成本），并加上subF[1]的利润（因为x购买后，其下属可享受折扣，故使用subF[1]，对应下属的上司购买状态）。
       • 对于每个预算j（从cost到budget），更新利润：f[k][j] = max(f[k][j], subF[1][j - cost] + (future[x] - cost))。

5. 根节点处理与结果提取：

   • 从根节点（员工0，即CEO）开始递归调用dfs(0)。由于根节点没有上司，其状态视为上司不购买（即使用k = 0）。
   • 最终，返回dfs(0)[0]数组中的最大值，即在预算范围内能获得的最大总利润。

复杂度分析

• 时间复杂度：算法对每个节点处理一次。对于每个节点x，需要合并其所有子节点的利润，合并过程中需要遍历预算j（0到budget）和子节点预算jy（0到j），因此每个节点的处理时间为O(m × budget²)，其中m是x的子节点数量。由于每个节点仅被处理一次，总时间复杂度为O(n × budget²)。其中n ≤ 160，budget ≤ 160，因此最坏情况下约为160³ = 4,096,000次操作，在合理范围内。
• 额外空间复杂度：主要空间用于存储树结构邻接表（O(n)）和递归DFS的栈空间（O(n)）。此外，每个节点需要两个大小为budget + 1的数组存储状态，因此总空间复杂度为O(n × budget)。代入n和budget的上限，约为O(160 × 160) = O(25,600)。

此方法通过树形DP和背包合并高效地解决了带有折扣规则的股票利润最大化问题，确保在预算约束下找到最优解。

Go完整代码如下：

package main

import (
	"fmt"
	"math"
	"slices"
)

func maxProfit(n int, present []int, future []int, hierarchy [][]int, budget int) int {
	g := make([][]int, n)
	for _, e := range hierarchy {
		x, y := e[0]-1, e[1]-1
		g[x] = append(g[x], y)
	}

	var dfs func(int) [2][]int
	dfs = func(x int) [2][]int {
		// 计算从 x 的所有儿子子树 y 中，能得到的最大利润之和
		subF := [2][]int{make([]int, budget+1), make([]int, budget+1)}
		for i := 1; i <= budget; i++ {
			subF[0][i] = math.MinInt / 2 // 表示不存在对应的花费总和
			subF[1][i] = math.MinInt / 2
		}
		for _, y := range g[x] {
			fy := dfs(y)
			for k, fyk := range fy {
				nf := make([]int, budget+1)
				for i := 1; i <= budget; i++ {
					nf[i] = math.MinInt / 2
				}
				for jy, resY := range fyk {
					if resY < 0 { // 重要优化：物品价值为负数，一定不选
						continue
					}
					for j := jy; j <= budget; j++ {
						nf[j] = max(nf[j], subF[k][j-jy]+resY)
					}
				}
				subF[k] = nf
			}
		}

		f := [2][]int{}
		for k := range 2 {
			// 不买 x，转移来源为 subF[0]，因为对于子树来说，父节点一定不买
			f[k] = slices.Clone(subF[0])
			cost := present[x] / (k + 1)
			// 买 x，转移来源为 subF[1]，因为对于子树来说，父节点一定买
			for j := cost; j <= budget; j++ {
				f[k][j] = max(f[k][j], subF[1][j-cost]+future[x]-cost)
			}
		}
		return f
	}

	return slices.Max(dfs(0)[0])
}

func main() {
	n := 3
	present := []int{4, 6, 8}
	future := []int{7, 9, 11}
	hierarchy := [][]int{{1, 2}, {1, 3}}
	budget := 10
	result := maxProfit(n, present, future, hierarchy, budget)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

import math
from typing import List

def maxProfit(n: int, present: List[int], future: List[int], hierarchy: List[List[int]], budget: int) -> int:
    # 构建邻接表表示的树结构
    g = [[] for _ in range(n)]
    for e in hierarchy:
        x, y = e[0] - 1, e[1] - 1
        g[x].append(y)
    
    def dfs(x: int) -> List[List[int]]:
        # subF[0] 和 subF[1] 分别表示不买和买当前节点时的状态
        subF = [[-10**9] * (budget + 1) for _ in range(2)]
        
        # 初始化：预算为0时利润为0
        for i in range(2):
            subF[i][0] = 0
        
        # 遍历所有子节点
        for y in g[x]:
            fy = dfs(y)
            # 对每个状态（0: 不买, 1: 买）
            for k in range(2):
                nf = [-10**9] * (budget + 1)
                nf[0] = 0
                
                # 遍历子节点的所有可能预算分配
                for jy in range(budget + 1):
                    resY = fy[k][jy]
                    if resY < 0:  # 重要优化：利润为负，一定不选
                        continue
                    # 更新当前预算下的最大利润
                    for j in range(jy, budget + 1):
                        if subF[k][j - jy] >= 0:
                            nf[j] = max(nf[j], subF[k][j - jy] + resY)
                
                subF[k] = nf
        
        # 计算当前节点的最终状态
        f = [[-10**9] * (budget + 1) for _ in range(2)]
        
        for k in range(2):
            # 不买当前节点：从子节点状态0转移
            f[k] = subF[0][:]
            
            # 买当前节点：从子节点状态1转移
            cost = present[x] // (k + 1)
            for j in range(cost, budget + 1):
                if subF[1][j - cost] >= 0:
                    profit = future[x] - cost
                    f[k][j] = max(f[k][j], subF[1][j - cost] + profit)
        
        return f
    
    result = dfs(0)
    return max(result[0])

def main():
    n = 3
    present = [4, 6, 8]
    future = [7, 9, 11]
    hierarchy = [[1, 2], [1, 3]]
    budget = 10
    result = maxProfit(n, present, future, hierarchy, budget)
    print(result)

if __name__ == "__main__":
    main()

C++完整代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
#include <limits>

using namespace std;

const int NEG_INF = numeric_limits<int>::min() / 2; // 相当于 math.MinInt / 2

int n_global, budget_global;
vector<int> present_global, future_global;
vector<vector<int>> g_global;

// DFS 返回两个 dp 数组：
// first = 父节点不买的情况下本节点子树的最优值
// second = 父节点买的情况下本节点子树的最优值
pair<vector<int>, vector<int>> dfs(int x) {
    // 初始化 subF[0] 和 subF[1]
    vector<int> subF0(budget_global + 1, NEG_INF);
    vector<int> subF1(budget_global + 1, NEG_INF);
    subF0[0] = 0;
    subF1[0] = 0;

    // 遍历所有孩子
    for (int y : g_global[x]) {
        auto fy = dfs(y);
        for (int k = 0; k <= 1; k++) {
            vector<int> nf(budget_global + 1, NEG_INF);
            const vector<int>& fyk = (k == 0 ? fy.first : fy.second);
            for (int jy = 0; jy <= budget_global; jy++) {
                int resY = fyk[jy];
                if (resY < 0) continue; // 负值不选
                for (int j = jy; j <= budget_global; j++) {
                    if (k == 0) {
                        nf[j] = max(nf[j], subF0[j - jy] + resY);
                    } else {
                        nf[j] = max(nf[j], subF1[j - jy] + resY);
                    }
                }
            }
            if (k == 0) subF0 = nf;
            else subF1 = nf;
        }
    }

    // f[0] 和 f[1] 分别对应 dfs 返回的两个向量
    vector<int> f0 = subF0;
    vector<int> f1 = subF0; // 克隆 subF0

    for (int k = 0; k <= 1; k++) {
        int cost = present_global[x] / (k + 1);
        for (int j = cost; j <= budget_global; j++) {
            if (subF1[j - cost] > NEG_INF / 2) { // 有效状态
                int profit = future_global[x] - cost;
                if (k == 0) {
                    f0[j] = max(f0[j], subF1[j - cost] + profit);
                } else {
                    f1[j] = max(f1[j], subF1[j - cost] + profit);
                }
            }
        }
    }

    return {f0, f1};
}

int maxProfit(int n, const vector<int>& present, const vector<int>& future,
              const vector<pair<int,int>>& hierarchy, int budget) {
    g_global.assign(n, {});
    for (auto &e : hierarchy) {
        int x = e.first - 1;
        int y = e.second - 1;
        g_global[x].push_back(y);
    }
    n_global = n;
    budget_global = budget;
    present_global = present;
    future_global = future;

    auto f = dfs(0);
    return *max_element(f.first.begin(), f.first.end());
}

int main() {
    int n = 3;
    vector<int> present = {4, 6, 8};
    vector<int> future = {7, 9, 11};
    vector<pair<int,int>> hierarchy = {{1, 2}, {1, 3}};
    int budget = 10;

    int result = maxProfit(n, present, future, hierarchy, budget);
    cout << result << endl; // 输出与 Go 程序一致
    return 0;
}