2025-11-10：给边赋权值的方案数Ⅱ。用go语言，给一棵以节点 1 为根的无向树，共 n 个节点，边集由长度为 n−1 的数组 edges 给出（edges[i] = [ui, vi] 表示 ui 与 vi 之间有条边）。起初每条边的权重为 0，你可以把任意边的权重改为 1 或 2。

对于一次查询 queries[i] = [ui, vi]，只看 ui 到 vi 这条唯一路径上的边（忽略树上其它边），统计把这些边的权重从 {1,2} 中选择，使得这条路径上所有边权重之和为奇数的不同赋值方案数。对每个查询都返回这样的方案数，结果对 1000000007 取模。

补充说明：若路径上有 m 条边，则答案为 2^{m-1}（对 1000000007 取模），因为每条边独立取 1 或 2，和的奇偶只取决于取 1 的边数，恰好有一半的赋值使和为奇数。

2 <= n <= 100000。

edges.length == n - 1。

edges[i] == [ui, vi]。

1 <= queries.length <= 100000。

queries[i] == [ui, vi]。

1 <= ui, vi <= n。

edges 表示一棵合法的树。

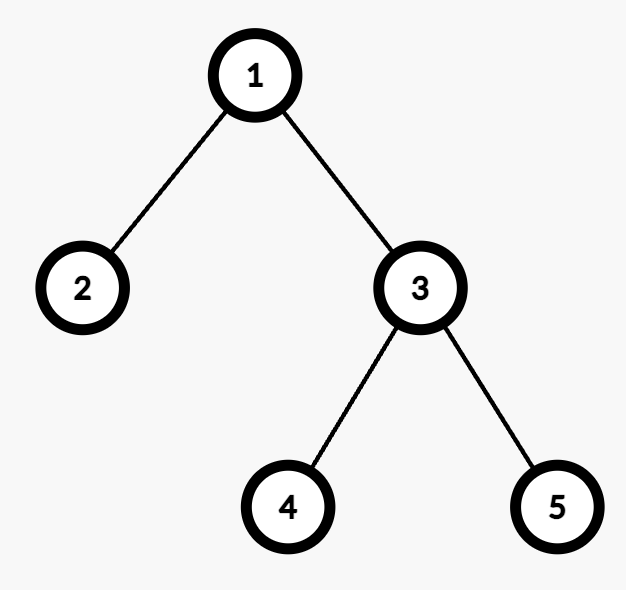
输入： edges = [[1,2],[1,3],[3,4],[3,5]], queries = [[1,4],[3,4],[2,5]]。

输出： [2,1,4]。

解释：

查询 [1,4]：路径为两条边（1 → 3 和 3 → 4），(1,2) 或 (2,1) 的组合会使代价为奇数，共 2 种。

查询 [3,4]：路径为一条边（3 → 4），仅权重为 1 时代价为奇数，共 1 种。

查询 [2,5]：路径为三条边（2 → 1 → 3 → 5），组合 (1,2,2)、(2,1,2)、(2,2,1)、(1,1,1) 均为奇数代价，共 4 种。

题目来自力扣3559。

解决过程

1. 预处理2的幂次

代码首先预处理了一个数组 pow2，其中 pow2[i] 存储了 (2^i \mod 1,000,000,007) 的值。这是为了后续快速计算方案数，因为每个查询的答案可以表示为 (2^{m-1})，其中 (m) 是路径上的边数。

2. 构建树结构

根据输入的边数组 edges，构建树的邻接表表示 g。每个节点都有一个列表存储其相邻节点，建立无向图结构以便后续遍历。

3. 深度优先搜索与预处理父节点信息

• 执行DFS从根节点（节点0，即题目中的节点1）开始遍历整棵树，计算每个节点的深度 dep。
• 同时构建倍增数组 pa，其中 pa[x][i] 存储节点 x 的第 (2^i) 级祖先节点。这为后续快速计算LCA（最近公共祖先）做准备。

4. 完善倍增数组

通过动态规划填充完整的倍增数组 pa：对于每个节点 x 和每个层级 i，pa[x][i+1] = pa[pa[x][i]][i]。这样可以在对数时间内查询任意节点的任意级祖先。

5. 实现LCA查询功能

包含三个关键函数：

• uptoDep(x, d): 将节点 x 提升到指定深度 d 的祖先节点。
• getLCA(x, y): 找到两个节点的最近公共祖先。首先将较深的节点提升到同一深度，然后同时向上跳跃直到找到LCA。
• getDis(x, y): 计算两节点间的距离（边数），公式为 dep[x] + dep[y] - 2*dep[lca]。

6. 处理查询

对于每个查询 [ui, vi]：

• 如果起点终点相同（路径边数m=0），答案为0。
• 否则计算两节点间的距离（边数）m，答案即为 pow2[m-1]。这是因为在m条边中，需要选择奇数条边赋值为1，这样的选择方案数正好是 (2^{m-1})。

复杂度分析

时间复杂度

• 预处理阶段:
  • DFS遍历: O(n)
  • 倍增数组构建: O(n log n)
• 查询处理:
  • 每个查询的LCA计算: O(log n)
  • k个查询总计: O(k log n)
• 总时间复杂度: O(n log n + k log n)

空间复杂度

• 邻接表: O(n)
• 深度数组: O(n)
• 倍增数组: O(n log n)
• 总空间复杂度: O(n log n)

这种基于LCA的解决方案能够高效处理大规模树上的路径查询问题。

Go完整代码如下：

package main

import (
	"fmt"
	"math/bits"
)

const mod = 1_000_000_007

var pow2 = [1e5]int{1}

func init() {
	// 预处理 2 的幂
	for i := 1; i < len(pow2); i++ {
		pow2[i] = pow2[i-1] * 2 % mod
	}
}

func assignEdgeWeights(edges [][]int, queries [][]int) []int {
	n := len(edges) + 1
	g := make([][]int, n)
	for _, e := range edges {
		x, y := e[0]-1, e[1]-1
		g[x] = append(g[x], y)
		g[y] = append(g[y], x)
	}

	const mx = 17
	pa := make([][mx]int, n)
	dep := make([]int, n)
	var dfs func(int, int)
	dfs = func(x, p int) {
		pa[x][0] = p
		for _, y := range g[x] {
			if y != p {
				dep[y] = dep[x] + 1
				dfs(y, x)
			}
		}
	}
	dfs(0, -1)
	for i := range mx - 1 {
		for x := range pa {
			if p := pa[x][i]; p != -1 {
				pa[x][i+1] = pa[p][i]
			} else {
				pa[x][i+1] = -1
			}
		}
	}
	uptoDep := func(x, d int) int {
		for k := uint(dep[x] - d); k > 0; k &= k - 1 {
			x = pa[x][bits.TrailingZeros(k)]
		}
		return x
	}
	getLCA := func(x, y int) int {
		if dep[x] > dep[y] {
			x, y = y, x
		}
		y = uptoDep(y, dep[x])
		if y == x {
			return x
		}
		for i := mx - 1; i >= 0; i-- {
			if pv, pw := pa[x][i], pa[y][i]; pv != pw {
				x, y = pv, pw
			}
		}
		return pa[x][0]
	}
	getDis := func(x, y int) int { return dep[x] + dep[y] - dep[getLCA(x, y)]*2 }

	ans := make([]int, len(queries))
	for i, q := range queries {
		if q[0] != q[1] {
			ans[i] = pow2[getDis(q[0]-1, q[1]-1)-1]
		}
	}
	return ans
}

func main() {
	edges := [][]int{{1, 2}, {1, 3}, {3, 4}, {3, 5}}
	queries := [][]int{{1, 4}, {3, 4}, {2, 5}}
	result := assignEdgeWeights(edges, queries)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

import sys
sys.setrecursionlimit(300000)
MOD = 1_000_000_007

class TreeLCA:
    def __init__(self, n, edges):
        self.n = n
        self.g = [[] for _ in range(n)]
        for x, y in edges:
            self.g[x].append(y)
            self.g[y].append(x)
        
        # 预处理2的幂
        self.pow2 = [1] * (n + 1)
        for i in range(1, n + 1):
            self.pow2[i] = self.pow2[i-1] * 2 % MOD
        
        # LCA相关数组
        self.mx = 17  # 2^17 > 1e5
        self.pa = [[-1] * self.mx for _ in range(n)]
        self.dep = [0] * n
        
        # DFS预处理
        self.dfs(0, -1)
        
        # 倍增预处理
        for i in range(self.mx - 1):
            for x in range(n):
                if self.pa[x][i] != -1:
                    self.pa[x][i+1] = self.pa[self.pa[x][i]][i]
                else:
                    self.pa[x][i+1] = -1
    
    def dfs(self, x, p):
        self.pa[x][0] = p
        for y in self.g[x]:
            if y != p:
                self.dep[y] = self.dep[x] + 1
                self.dfs(y, x)
    
    def upto_dep(self, x, d):
        """将节点x向上移动到深度d的位置"""
        k = self.dep[x] - d
        while k > 0:
            i = k & -k
            x = self.pa[x][i.bit_length() - 1]
            k -= i
        return x
    
    def get_lca(self, x, y):
        """获取x和y的最近公共祖先"""
        if self.dep[x] > self.dep[y]:
            x, y = y, x
        y = self.upto_dep(y, self.dep[x])
        if y == x:
            return x
        
        for i in range(self.mx - 1, -1, -1):
            if self.pa[x][i] != self.pa[y][i]:
                x = self.pa[x][i]
                y = self.pa[y][i]
        return self.pa[x][0]
    
    def get_dis(self, x, y):
        """获取x和y之间的距离"""
        lca = self.get_lca(x, y)
        return self.dep[x] + self.dep[y] - 2 * self.dep[lca]

def assign_edge_weights(edges, queries):
    n = len(edges) + 1
    # 将节点编号从1-based转换为0-based
    converted_edges = [[x-1, y-1] for x, y in edges]
    
    tree = TreeLCA(n, converted_edges)
    
    ans = []
    for q in queries:
        u, v = q[0]-1, q[1]-1
        if u == v:
            ans.append(0)
        else:
            dis = tree.get_dis(u, v)
            ans.append(tree.pow2[dis - 1])
    
    return ans

def main():
    edges = [[1, 2], [1, 3], [3, 4], [3, 5]]
    queries = [[1, 4], [3, 4], [2, 5]]
    result = assign_edge_weights(edges, queries)
    print(result)

if __name__ == "__main__":
    main()

C++完整代码如下：

#include <iostream>
#include <vector>
#include <array>
#include <algorithm>

using namespace std;

const int MOD = 1000000007;
const int MX = 17;           // 最大二进制跳跃深度
const int NMAX = 100000;     // 最大节点数（用于 pow2 预处理）

vector<int> pow2(NMAX, 1);   // 存储 2^k % MOD
vector<vector<int>> g;       // 邻接表
vector<array<int, MX>> pa;   // 父节点表
vector<int> dep;             // 节点深度

// 初始化 pow2 数组
void init_pow2() {
    for (int i = 1; i < NMAX; i++) {
        pow2[i] = (1LL * pow2[i - 1] * 2) % MOD;
    }
}

// DFS 建立父节点表和深度
void dfs(int x, int p) {
    pa[x][0] = p;
    for (int y : g[x]) {
        if (y != p) {
            dep[y] = dep[x] + 1;
            dfs(y, x);
        }
    }
}

// 跳到目标深度
int uptoDep(int x, int d) {
    int k = dep[x] - d;
    while (k > 0) {
        int t = __builtin_ctz(k); // 求最低位 1 的位置（MinGW 支持）
        x = pa[x][t];
        k &= (k - 1);
    }
    return x;
}

// 求 LCA
int getLCA(int x, int y) {
    if (dep[x] > dep[y]) swap(x, y);
    y = uptoDep(y, dep[x]);
    if (x == y) return x;
    for (int i = MX - 1; i >= 0; i--) {
        if (pa[x][i] != pa[y][i]) {
            x = pa[x][i];
            y = pa[y][i];
        }
    }
    return pa[x][0];
}

// 求两点距离
int getDis(int x, int y) {
    int lca = getLCA(x, y);
    return dep[x] + dep[y] - dep[lca] * 2;
}

// 主计算函数
vector<int> assignEdgeWeights(const vector<pair<int,int>> &edges,
                              const vector<pair<int,int>> &queries) {
    int n = edges.size() + 1;
    g.assign(n, {});
    pa.assign(n, {});
    dep.assign(n, 0);

    // 建树
    for (auto &e : edges) {
        int x = e.first - 1;
        int y = e.second - 1;
        g[x].push_back(y);
        g[y].push_back(x);
    }

    // DFS 建立父节点表
    dfs(0, -1);

    // 预处理二进制跳跃表
    for (int j = 1; j < MX; j++) {
        for (int i = 0; i < n; i++) {
            if (pa[i][j-1] != -1)
                pa[i][j] = pa[pa[i][j-1]][j-1];
            else
                pa[i][j] = -1;
        }
    }

    vector<int> ans(queries.size());
    for (size_t i = 0; i < queries.size(); i++) {
        int u = queries[i].first - 1;
        int v = queries[i].second - 1;
        if (u != v) {
            ans[i] = pow2[getDis(u, v) - 1];
        } else {
            ans[i] = 0;
        }
    }
    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    init_pow2();

    vector<pair<int,int>> edges = {{1,2},{1,3},{3,4},{3,5}};
    vector<pair<int,int>> queries = {{1,4},{3,4},{2,5}};

    vector<int> result = assignEdgeWeights(edges, queries);

    for (int val : result) {
        cout << val << " ";
    }
    cout << "\n";

    return 0;
}