2025-11-09：给边赋权值的方案数Ⅰ。用go语言，给定一棵以节点 1 为根的无向树，共 n 个节点，边由长度为 n−1 的数组 edges 给出（每个元素 [u,v] 表示 u 与 v 之间有一条边）。起初所有边的权重为 0，但你可以把每条边设为权值 1 或 2。

任选一个与根节点 1 距离最大的节点 x（即最远的节点）。只看从节点 1 到该节点 x 的那条简单路径（路径之外的边不参与计数），统计有多少种将该路径上每条边的权值设为 1 或 2 的方法，使得从 1 到 x 的边权总和为奇数。

结果要求对 1000000007 取模后输出。

2 <= n <= 100000。

edges.length == n - 1。

edges[i] == [ui, vi]。

1 <= ui, vi <= n。

edges 表示一棵合法的树。

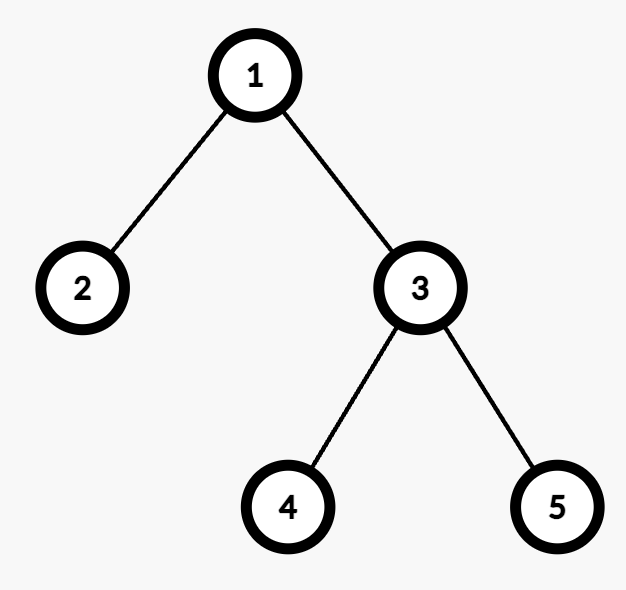
输入： edges = [[1,2],[1,3],[3,4],[3,5]]。

输出： 2。

解释：

最大深度为 2，节点 4 和节点 5 都在该深度，可以选择任意一个。

例如，从节点 1 到节点 4 的路径包括两条边（1 → 3 和 3 → 4）。

将两条边赋权为 (1,2) 或 (2,1) 会使代价为奇数，因此合法赋值方式有 2 种。

题目来自力扣3558。

问题分析过程

这个问题要求计算在树结构中，从根节点到最深叶子节点的路径上，通过给边赋权值1或2，使得路径总权值为奇数的方案数。以下是详细的分步分析：

1. 构建树结构

首先需要根据输入的边数组构建树的邻接表表示。由于树是无向的，每条边需要在两个节点的邻接表中都添加对方节点，从而形成完整的连通图结构。

2. 计算最大深度

通过深度优先搜索（DFS）从根节点（节点1）开始遍历整棵树，计算每个节点的深度（到根节点的距离）。在DFS过程中，维护当前深度信息，递归访问每个未访问过的子节点（避免回溯到父节点），最终得到整棵树的最大深度k。

3. 确定路径边数

从根节点到最深节点x的路径边数等于最大深度k（因为深度是从根节点开始计算的节点层数，边数比深度少1）。因此实际需要赋权的边数为n = k-1。

4. 分析权值赋值方案

路径总权值为奇数的条件等价于路径上权值为1的边必须有奇数条（因为每条边权值只能是1或2，而2不会改变总和的奇偶性）。问题转化为：在n条边中选择奇数条边赋权为1，其余赋权为2。

5. 计算方案数

组合数学结论：从n条边中选择奇数条边的方案总数为2^(n-1)。这可以通过二项式定理证明：选择奇数个元素的方案数等于2^(n-1)。

6. 快速幂取模

由于n可能很大（最大99999），直接计算2^(n-1)会溢出。使用快速幂算法，在O(log n)时间内完成模幂运算，结果对1,000,000,007取模。

复杂度分析

时间复杂度：O(n)

• 构建邻接表：O(n)，需要处理n-1条边
• DFS遍历：O(n)，每个节点访问一次
• 快速幂计算：O(log n)，相对于线性可忽略
• 总体以DFS为主导，故为O(n)

空间复杂度：O(n)

• 邻接表存储：O(n)，存储n个节点的邻接关系
• DFS递归栈：最坏情况O(n)（当树退化为链时）
• 其他变量：O(1)
• 总体空间消耗与节点数n成正比

这个解决方案高效地结合了树遍历和组合数学，通过一次DFS确定关键路径长度，再利用数学结论直接计算结果，避免了枚举所有可能的权值分配方案。

Go完整代码如下：

package main

import (
	"fmt"
)

func assignEdgeWeights(edges [][]int) int {
	n := len(edges) + 1
	g := make([][]int, n+1)
	for _, e := range edges {
		x, y := e[0], e[1]
		g[x] = append(g[x], y)
		g[y] = append(g[y], x)
	}

	var dfs func(int, int) int
	dfs = func(x, fa int) (d int) {
		for _, y := range g[x] {
			if y != fa { // 不递归到父节点
				d = max(d, dfs(y, x)+1)
			}
		}
		return
	}

	k := dfs(1, 0)
	return pow(2, k-1)
}

func pow(x, n int) int {
	const mod = 1_000_000_007
	res := 1
	for ; n > 0; n /= 2 {
		if n%2 > 0 {
			res = res * x % mod
		}
		x = x * x % mod
	}
	return res
}

func main() {
	edges := [][]int{{1, 2}, {1, 3}, {3, 4}, {3, 5}}
	result := assignEdgeWeights(edges)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

from typing import List

def assignEdgeWeights(edges: List[List[int]]) -> int:
    n = len(edges) + 1
    g = [[] for _ in range(n + 1)]
    for e in edges:
        x, y = e[0], e[1]
        g[x].append(y)
        g[y].append(x)
    
    def dfs(x: int, fa: int) -> int:
        d = 0
        for y in g[x]:
            if y != fa:  # 不递归到父节点
                d = max(d, dfs(y, x) + 1)
        return d
    
    k = dfs(1, 0)
    return pow(2, k - 1)

def main():
    edges = [[1, 2], [1, 3], [3, 4], [3, 5]]
    result = assignEdgeWeights(edges)
    print(result)

if __name__ == "__main__":
    main()

C++完整代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>

using namespace std;

int pow_mod(int x, int n, int mod) {
    long long res = 1;
    long long base = x;
    while (n > 0) {
        if (n % 2 == 1) {
            res = (res * base) % mod;
        }
        base = (base * base) % mod;
        n /= 2;
    }
    return res;
}

int assignEdgeWeights(vector<vector<int>>& edges) {
    int n = edges.size() + 1;
    vector<vector<int>> g(n + 1);
    for (auto& e : edges) {
        int x = e[0], y = e[1];
        g[x].push_back(y);
        g[y].push_back(x);
    }
    
    function<int(int, int)> dfs = [&](int x, int fa) -> int {
        int d = 0;
        for (int y : g[x]) {
            if (y != fa) { // 不递归到父节点
                d = max(d, dfs(y, x) + 1);
            }
        }
        return d;
    };
    
    int k = dfs(1, 0);
    return pow_mod(2, k - 1, 1000000007);
}

int main() {
    vector<vector<int>> edges = {{1, 2}, {1, 3}, {3, 4}, {3, 5}};
    int result = assignEdgeWeights(edges);
    cout << result << endl;
    return 0;
}