2025-10-27：K 条边路径的最大边权和。用go语言，给定一个有向无环图（节点编号为 0 到 n−1），图的边用一个二维数组 edges 表示，其中每个元素 edges[i] = [u_i, v_i, w_i] 表示从 u_i 指向 v_i 的一条边，权重为 w_i。还给出两个整数 k 和 t。

要求找出一条满足下列条件的路径：

• 路径恰好包含 k 条边；

• 路径上所有边的权重之和小于 t（不能等于 t）；

在满足以上条件的所有路径中，选择边权和最大的那一条，并返回该最大和。如果不存在任何符合条件的路径，则返回 -1。

1 <= n <= 300。

0 <= edges.length <= 300。

edges[i] = [ui, vi, wi]。

0 <= ui, vi < n。

ui != vi。

1 <= wi <= 10。

0 <= k <= 300。

1 <= t <= 600。

输入图是 有向无环图（DAG）。

不存在重复的边。

输入: n = 3, edges = [[0,1,1],[1,2,2]], k = 2, t = 4。

输出: 3。

解释:

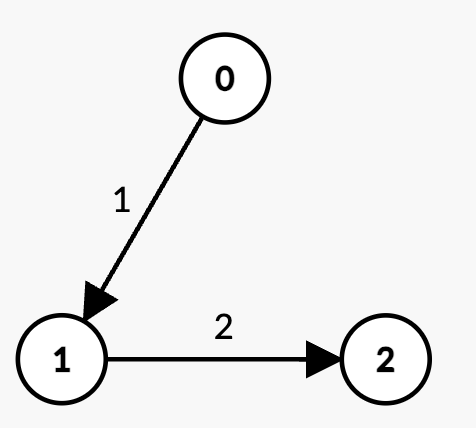
唯一包含 k = 2 条边的路径是 0 -> 1 -> 2，其权重和为 1 + 2 = 3 < t。

因此，最大可能的边权和为 3。

题目来自力扣3544。

🔄 动态规划状态设计

我们定义一个二维 DP 数组 f[i][x]，其含义如下：

• i：表示路径已经走过的边数。
• x：表示当前路径到达的节点编号。
• f[i][x]：这是一个 big.Int，它作为一个位掩码（Bit Mask）。这个整数中的每一个二进制位代表一个可能的路径权重和。如果某个权重和 s 是可达的，那么从节点 x 出发，经过恰好 i 条边能够达到这个权重和 s，则 f[i][x] 的第 s 位会被设置为 1。

这种设计巧妙地利用了位图来压缩表示所有可能的路径和，避免了显式地存储每一个数值。

🧩 算法步骤详解

1. 初始化

   • 首先检查节点数 n 是否小于等于边数 k。如果是，直接返回 -1，因为无法形成 k 条边的路径。
   • 创建 DP 表 f，大小为 (k+1) * n，并初始化为 0。
   • 对于 f[0][x]，即所有经过 0 条边到达节点 x 的状态。我们将所有 f[0][x] 的第0位设置为 1。这表示从任何节点本身出发（不经过任何边），路径和是 0，这是一个合法的起点状态。

2. 状态转移：逐边扩展路径
   这是算法的核心循环。我们遍历边数 i 从 0 到 k-1，对于每个状态 f[i][x]，我们检查所有从节点 x 出发的边 (x, y, wt)。

   • 核心操作：对于 f[i][x] 中每一个已置位的权重和 s（即存在一条到 x 的 i 边路径，和为 s），我们可以通过加上当前边的权重 wt，得到一条到 y 的 i+1 边路径，其新权重和为 s + wt。
   • 位运算实现：这个转移通过位运算高效完成。将 f[i][x] 这个位掩码左移 wt 位，相当于将所有已存在的路径和都增加了 wt。然后，使用 按位或（OR） 操作将这个新的状态合并到 f[i+1][y] 中，表示这些新的路径和也是可达的。
   • 约束处理：为了确保路径和严格小于 t，我们创建了一个掩码 mask = (1 << t) - 1。在左移后，通过按位与（AND） 操作与这个掩码进行运算。这样可以过滤掉所有大于等于 t 的路径和（因为它们会移位到第 t 位及更高位，而被掩码截断），只保留我们关心的部分。

3. 提取最终结果
   在所有状态转移完成后，我们检查 f[k][x]，即所有恰好包含 k 条边且终点为任意节点 x 的路径状态。

   • 我们遍历 f[k][x] 中的每一个 big.Int。
   • 利用 big.Int 的 BitLen() 方法，可以找到这个位掩码中最高位被置1的位置。这个位置减 1（因为位数从0开始计算）就代表了所有可达路径中的最大权重和。
   • 如果所有 f[k][x] 都是 0（BitLen() 返回 0），说明没有符合条件的路径，返回 -1。

⏱️ 复杂度分析

• 时间复杂度：该算法的时间复杂度主要由三重循环决定：

  1. 外层循环遍历边数，从 0 到 k-1，共 k 次。
  2. 中层循环遍历所有边，共 E 次（E 为边的数量）。
  3. 内层操作是 big.Int 的位运算（左移、按位与、按位或），这些操作的时间复杂度与 big.Int 的位数（大致与 t 成正比）有关。
     因此，总的时间复杂度为 O(k * E * t)。考虑到题目中 n, k, E 的最大值均为 300，t 的最大值为 600，这个复杂度在可接受范围内。

• 空间复杂度：空间开销主要用于存储 DP 表 f。表的大小为 (k+1) * n，每个元素是一个 big.Int，其占用的空间与 t 成正比（因为需要表示 0 到 t-1 位）。因此，总的空间复杂度为 O(k * n * t)。

💎 核心思路总结

这个方法的高明之处在于：

1. 状态压缩：使用一个整数的二进制位来标记大量离散的路径和是否可达，极大节省了空间。
2. 位运算批量处理：通过左移和按位操作，一次性完成一整批路径状态的转移，提升了效率。
3. 利用DAG无环特性：由于图是无环的，按边数进行动态规划可以保证状态转移的正确性，不会出现无限循环。

希望这个分步详解能帮助你透彻地理解这个算法的原理和实现。

Go完整代码如下：

package main

import (
	"fmt"
	"math/big"
)

func maxWeight(n int, edges [][]int, k int, t int) int {
	if n <= k {
		return -1
	}

	f := make([][]*big.Int, k+1)
	for i := range f {
		f[i] = make([]*big.Int, n)
		for j := range f[i] {
			f[i][j] = big.NewInt(0)
		}
	}
	for i := range f[0] {
		f[0][i] = big.NewInt(1)
	}

	p := new(big.Int)
	mask := new(big.Int).Sub(p.Lsh(big.NewInt(1), uint(t)), big.NewInt(1))
	for i, fi := range f[:k] {
		for _, e := range edges {
			x, y, wt := e[0], e[1], e[2]
			if fi[x].Sign() != 0 {
				shifted := p.And(p.Lsh(fi[x], uint(wt)), mask)
				f[i+1][y].Or(f[i+1][y], shifted)
			}
		}
	}

	ans := 0
	for _, bi := range f[k] {
		ans = max(ans, bi.BitLen())
	}
	return ans - 1
}

func main() {
	n := 3
	edges := [][]int{{0, 1, 1}, {1, 2, 2}}
	k := 2
	t := 4
	result := maxWeight(n, edges, k, t)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

def maxWeight(n, edges, k, t):
    if n <= k:
        return -1
    
    # 初始化DP数组，f[i][j]表示经过i条边到达节点j的权重状态
    f = [[0] * n for _ in range(k + 1)]
    
    # 初始化：经过0条边到达任何节点的权重为1（二进制表示）
    for i in range(n):
        f[0][i] = 1
    
    # 创建掩码用于限制位数
    mask = (1 << t) - 1
    
    # 动态规划
    for i in range(k):
        for edge in edges:
            x, y, wt = edge
            if f[i][x] != 0:
                # 左移权重位并与掩码取AND，然后与目标状态取OR
                shifted = (f[i][x] << wt) & mask
                f[i + 1][y] |= shifted
    
    # 寻找最大权重（最高位的位置）
    ans = 0
    for state in f[k]:
        if state == 0:
            continue
        # 计算二进制位数并减1得到最大权重
        bit_len = state.bit_length()
        ans = max(ans, bit_len - 1)
    
    return ans

def main():
    n = 3
    edges = [[0, 1, 1], [1, 2, 2]]
    k = 2
    t = 4
    result = maxWeight(n, edges, k, t)
    print(result)

if __name__ == "__main__":
    main()