2025-10-26：将所有元素变为 0 的最少操作次数。用go语言，给定一个长度为 n 的非负整数序列 nums。

每次操作你可以选取一个连续的区间 [i, j]，并将该区间内值等于该区间最小值的所有元素改为 0。

可以进行任意次这样的操作（也可以不做），目标是把数组中所有元素都变为 0。

请计算完成这一目标所需的最少操作次数。

1 <= n == nums.length <= 100000。

0 <= nums[i] <= 100000。

输入: nums = [1,2,1,2,1,2]。

输出: 4。

解释:

选择子数组 [0,5]（即 [1,2,1,2,1,2]），最小非负整数是 1。将所有 1 设为 0，结果为 [0,2,0,2,0,2]。

选择子数组 [1,1]（即 [2]），将 2 设为 0，结果为 [0,0,0,2,0,2]。

选择子数组 [3,3]（即 [2]），将 2 设为 0，结果为 [0,0,0,0,0,2]。

选择子数组 [5,5]（即 [2]），将 2 设为 0，结果为 [0,0,0,0,0,0]。

因此，最少操作次数为 4。

题目来自力扣3542。

算法思路（单调栈 + 贪心）

这个解法采用单调栈思想，一次遍历数组，并利用“相邻相同元素可以在同一次操作中删除”的性质来减少操作次数。

步骤描述

1. 初始化

   • 使用 st 作为单调栈（这里直接复用 nums 的前部分空间来节省内存，即原地修改）。
   • ans 记录操作次数，初始为 0。

2. 遍历数组元素
   对于每一个元素 x = nums[i]：

   • 情况 A：x 比栈顶元素小
     如果 x < st[len(st)-1]，说明栈顶元素在后续不会再成为某个区间的最小值（因为 x 更小，会先被处理），所以需要先单独处理栈顶元素。
     弹出栈顶元素，并且 ans++（表示需要一次操作来清除这个值）。
     重复此过程，直到栈为空或者 x >= st[len(st)-1]。

   • 情况 B：x 与栈顶元素相同
     如果 x == st[len(st)-1]，那么 x 可以和栈顶元素在同一次操作中一起被清除（因为它们值相同，可以在某个包含它们的区间内一次操作置 0），因此 x 不入栈。
     这样避免了重复计数操作。

   • 情况 C：x 大于栈顶元素或栈为空
     如果栈为空，或者 x > st[len(st)-1]，则 x 入栈。

3. 遍历结束后的处理
   栈中剩下的元素是非严格递增的（因为我们在遍历时已经去掉了比当前元素大的栈顶元素，并且相同的不入栈）。
   每个栈中元素都需要一次操作来清除，所以操作次数还要加上 len(st)。

4. 特殊情况：栈底是 0
   如果栈的第一个元素是 0，那么 0 不需要操作，所以 ans--（因为 0 本来就不需要清除，但之前统计操作次数时可能多算了一次）。

5. 最终答案
   ans + len(st) 就是最少操作次数。

以 nums = [1,2,1,2,1,2] 为例

初始：st = [], ans = 0

• x=1：栈空，入栈 → st = [1]
• x=2：2 > 1，入栈 → st = [1,2]
• x=1：1 < 2，弹出 2，ans++（=1），栈变 [1]；
  现在 1 == 1（与栈顶相同），所以 1 不入栈（它们可以在同一次操作中清除） → st = [1]
• x=2：2 > 1，入栈 → st = [1,2]
• x=1：1 < 2，弹出 2，ans++（=2），栈变 [1]；
  栈顶 1 == 1，所以 1 不入栈 → st = [1]
• x=2：2 > 1，入栈 → st = [1,2]

遍历结束：
st = [1,2]，ans = 2
最终操作次数 = ans + len(st) = 2 + 2 = 4
栈底 st[0] = 1 不是 0，所以不减。

输出：4

时间复杂度

• 每个元素最多入栈一次、出栈一次，所以时间复杂度是 O(n)。

空间复杂度

• 除了输入数组外，只用了几个变量，栈是原地复用 nums 的前部空间，所以额外空间复杂度是 O(1)。

总结
该算法通过单调栈维护一个非严格递增序列，并在遍历时利用“相同值可一次清除”的性质，高效地统计了最少操作次数，时间和空间复杂度都很优。

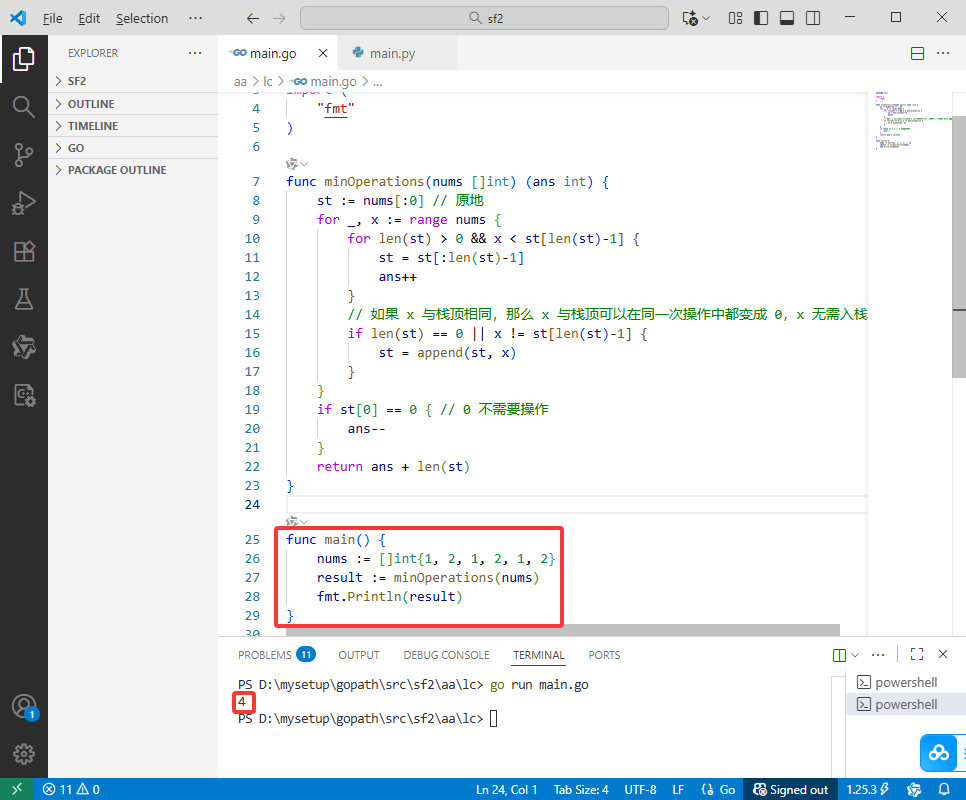
Go完整代码如下：

package main

import (
	"fmt"
)

func minOperations(nums []int) (ans int) {
	st := nums[:0] // 原地
	for _, x := range nums {
		for len(st) > 0 && x < st[len(st)-1] {
			st = st[:len(st)-1]
			ans++
		}
		// 如果 x 与栈顶相同，那么 x 与栈顶可以在同一次操作中都变成 0，x 无需入栈
		if len(st) == 0 || x != st[len(st)-1] {
			st = append(st, x)
		}
	}
	if st[0] == 0 { // 0 不需要操作
		ans--
	}
	return ans + len(st)
}

func main() {
	nums := []int{1, 2, 1, 2, 1, 2}
	result := minOperations(nums)
	fmt.Println(result)
}

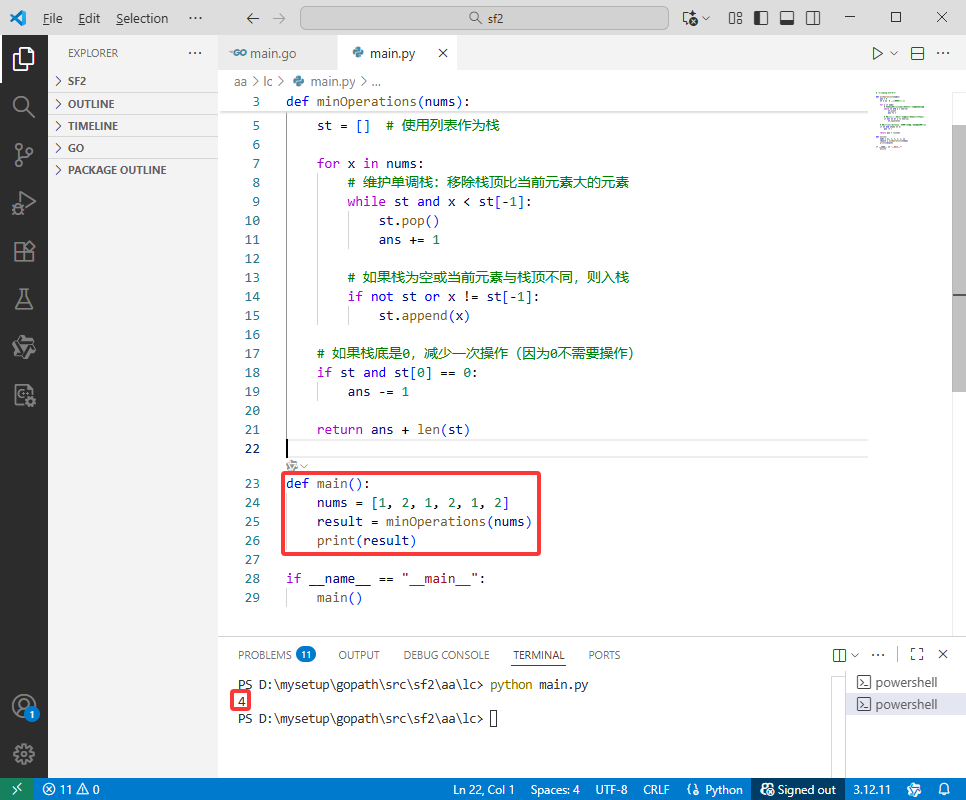
Python完整代码如下：

# -*-coding:utf-8-*-

def minOperations(nums):
    ans = 0
    st = []  # 使用列表作为栈
    
    for x in nums:
        # 维护单调栈：移除栈顶比当前元素大的元素
        while st and x < st[-1]:
            st.pop()
            ans += 1
        
        # 如果栈为空或当前元素与栈顶不同，则入栈
        if not st or x != st[-1]:
            st.append(x)
    
    # 如果栈底是0，减少一次操作（因为0不需要操作）
    if st and st[0] == 0:
        ans -= 1
    
    return ans + len(st)

def main():
    nums = [1, 2, 1, 2, 1, 2]
    result = minOperations(nums)
    print(result)

if __name__ == "__main__":
    main()