2025-10-22：填充特殊网格。用go语言，给定非负整数 N，要求构造一个边长为 $2^N$ 的方阵，用 0 到 $2^{2N}-1$ 这 $2^{2N}$ 个整数恰好一次地填满整个矩阵。把矩阵沿中线分成四个等大的子方阵（左上、右上、左下、右下），需要满足：

• 右上子方阵内的任意元素都小于右下子方阵内的任意元素；

• 右下子方阵内的任意元素都小于左下子方阵内的任意元素；

• 左下子方阵内的任意元素都小于左上子方阵内的任意元素；

• 并且这四个子方阵本身也要满足同样的性质（对更小尺寸继续递归）。

当 N=0（即 1×1 方格）时，条件自洽。输出满足上述所有条件的 $2^N × 2^N$ 方阵。
0 <= N <= 10。

输入： N = 2。

输出： [[15,12,3,0],[14,13,2,1],[11,8,7,4],[10,9,6,5]]。

解释：

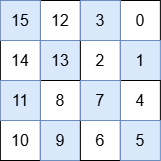
每个象限的数字如下：

右上角：3, 0, 2, 1

右下角：7, 4, 6, 5

左下角：11, 8, 10, 9

左上角：15, 12, 14, 13

max(3, 0, 2, 1) < min(7, 4, 6, 5)

max(7, 4, 6, 5) < min(11, 8, 10, 9)

max(11, 8, 10, 9) < min(15, 12, 14, 13)

这满足前三个要求。此外，每个象限也是一个特殊网格。因此，这是一个特殊网格。

题目来自力扣3537。

分步骤描述填充特殊网格的过程

填充特殊网格的过程基于分治策略和递归实现，核心思想是将大网格不断划分为更小的子网格，并按照特定顺序填充数字，以确保满足题目中的大小关系条件。以下是详细步骤：

1. 初始化阶段：

   • 创建一个大小为 (2^N \times 2^N) 的二维矩阵（方阵），所有元素初始值可设为0或占位符。
   • 初始化一个全局计数器 val（起始值为0），用于生成待填充的数字（从0到 (2^{2N}-1)）。

2. 递归填充函数的设计：

   • 定义递归函数 dfs，参数包括当前处理的子网格（通过行、列边界隐式定义）和当前层级的列偏移量 l（用于定位子网格的起始列）。
   • 终止条件：当当前子网格大小为 (1 \times 1)（即仅一个单元格）时，将计数器 val 的值填入该单元格，并执行 val++。
   • 递归划分：若子网格大小大于 (1 \times 1)，则计算当前网格边长的一半 (m = \text{len}(a) / 2)，将网格划分为四个等大的象限。

3. 递归填充顺序（关键步骤）：

   • 按特定顺序递归处理四个象限，确保填充后满足“右上 < 右下 < 左下 < 左上”的约束：
     • 第一步：填充右上象限
       对右上子网格（行范围：当前网格的前 m 行，列范围：从 l + m 开始的右半部分）递归调用 dfs。
     • 第二步：填充右下象限
       对右下子网格（行范围：后 m 行，列范围：从 l + m 开始的右半部分）递归调用 dfs。
     • 第三步：填充左下象限
       对左下子网格（行范围：后 m 行，列范围：从 l 开始的左半部分）递归调用 dfs。
     • 第四步：填充左上象限
       对左上子网格（行范围：前 m 行，列范围：从 l 开始的左半部分）递归调用 dfs。
   • 为什么此顺序有效：全局计数器 val 从0开始递增。先填充的象限获得较小的数字，后填充的获得较大的数字。因此，右上象限数字最小，右下次之，左下较大，左上最大，自然满足大小关系。每个象限内部继续递归应用相同规则，保证递归性质。

4. 填充示例（以 (N=2) 为例）：

   • 初始网格为 (4 \times 4)，第一次划分后 (m=2)。
   • 填充顺序：
     1. 右上象限（行0-1, 列2-3）填充数字0-3。
     2. 右下象限（行2-3, 列2-3）填充数字4-7。
     3. 左下象限（行2-3, 列0-1）填充数字8-11。
     4. 左上象限（行0-1, 列0-1）填充数字12-15。
   • 最终矩阵如题目示例所示，每个象限内数字也递归满足相同条件。

5. 终止与回溯：

   • 递归最终到达 (1 \times 1) 网格时直接赋值，无需进一步划分。
   • 所有递归调用完成后，矩阵填充结束。

时间复杂度和空间复杂度分析

• 时间复杂度：(O(4^N))
  算法需填充整个 (2^N \times 2^N) 网格的每个单元格，总单元格数为 (2^{2N} = 4^N)。每个单元格仅被访问一次并赋值，因此时间复杂度为 (O(4^N))。

• 额外空间复杂度：(O(N))

  • 主要来自递归调用栈的深度。每次递归将网格尺寸减半，递归深度为 (N)（因为 (2^N) 需经过 (N) 次划分才能到达 (1 \times 1)）。每层递归使用常数空间存储参数（如边界信息），因此栈空间复杂度为 (O(N))。
  • 全局计数器 val 占用 (O(1)) 空间。
  • 注意：输出矩阵本身占 (O(4^N)) 空间，但此为问题要求，不计入“额外”空间。

Go完整代码如下：

package main

import (
	"fmt"
)

func specialGrid(n int) [][]int {
	val := 0
	var dfs func([][]int, int)
	dfs = func(a [][]int, l int) {
		if len(a) == 1 {
			a[0][l] = val
			val++
			return
		}
		m := len(a) / 2
		dfs(a[:m], l+m)
		dfs(a[m:], l+m)
		dfs(a[m:], l)
		dfs(a[:m], l)
	}

	a := make([][]int, 1<<n)
	for i := range a {
		a[i] = make([]int, 1<<n)
	}
	dfs(a, 0)
	return a
}

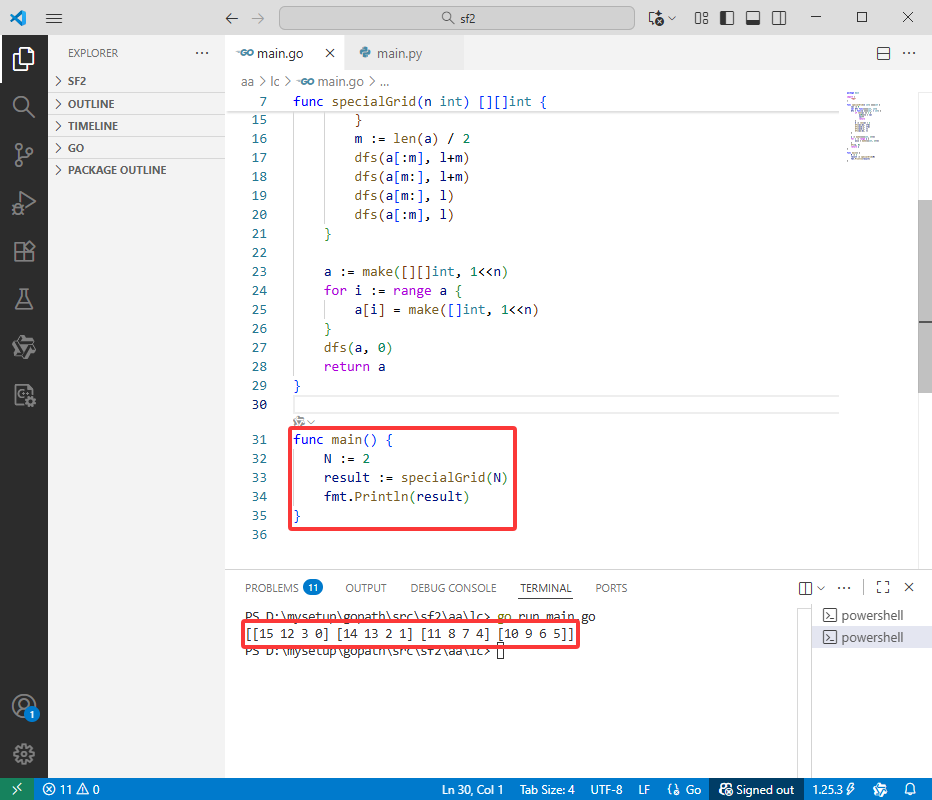
func main() {
	N := 2
	result := specialGrid(N)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

def special_grid(n):
    val = [0]  # 使用列表来模拟引用传递，以便在递归中修改
    
    def dfs(a, l):
        if len(a) == 1:
            a[0][l] = val[0]
            val[0] += 1
            return
        
        m = len(a) // 2
        dfs(a[:m], l + m)  # 右上
        dfs(a[m:], l + m)  # 右下  
        dfs(a[m:], l)      # 左下
        dfs(a[:m], l)      # 左上
    
    size = 1 << n
    a = [[0] * size for _ in range(size)]
    dfs(a, 0)
    return a

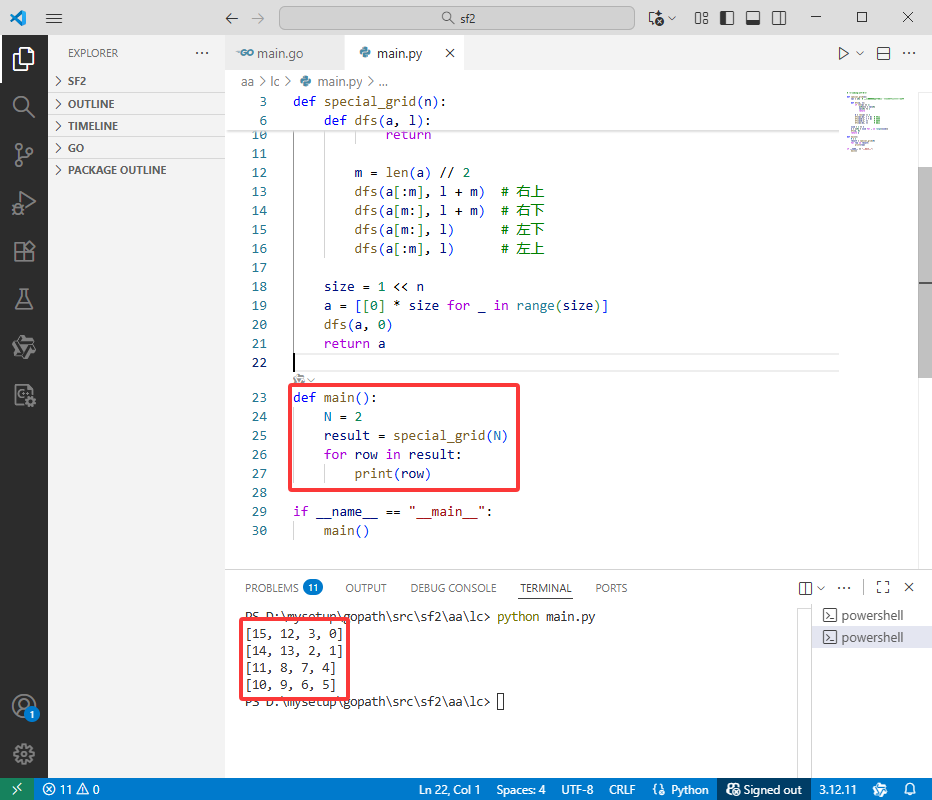
def main():
    N = 2
    result = special_grid(N)
    for row in result:
        print(row)

if __name__ == "__main__":
    main()