2025-10-17：统计被覆盖的建筑。用go语言，给定一个正整数 n，表示一个 n×n 的格子城市；同时给出一个数组 buildings，每个元素 buildings[i] = [x,y] 表示在坐标 (x,y) 处有一座建筑，且这些坐标互不重复。

如果某座建筑在它的上、下、左、右这四个方向上，沿各自的直线上至少还能找到另一座建筑，则称该建筑为“满足条件”。

要求返回满足该条件的建筑总数。

输入：正整数 n 和二维数组 buildings（坐标均为整数，通常落在 0 到 n−1 之间，且无重复）。

输出：一个整数，表示满足上述四个方向均有建筑这一条件的建筑数量。

2 <= n <= 100000。

1 <= buildings.length <= 100000。

buildings[i] = [x, y]。

1 <= x, y <= n。

buildings 中所有坐标均 唯一 。

输入: n = 3, buildings = [[1,1],[1,2],[2,1],[2,2]]。

输出: 0。

解释:

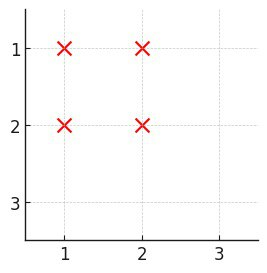
没有任何一个建筑在每个方向上都有至少一个建筑。

题目来自力扣3531。

解决步骤

1. 数据结构初始化

• 创建两个数组 row 和 col，长度均为 n+1（索引 1 到 n）。
• row[y] 存储行 y 上所有建筑的 x 坐标的最小值和最大值。
• col[x] 存储列 x 上所有建筑的 y 坐标的最小值和最大值。
• 初始时，每个 row[y].min 和 col[x].min 设为最大整数（表示尚未找到建筑），每个 row[y].max 和 col[x].max 设为最小整数（或 0，但后续会被覆盖）。

2. 收集每行和每列的信息

• 遍历所有建筑 (x, y)：
  • 更新 row[y].min 为 min(row[y].min, x)。
  • 更新 row[y].max 为 max(row[y].max, x)。
  • 更新 col[x].min 为 min(col[x].min, y)。
  • 更新 col[x].max 为 max(col[x].max, y)。
• 这样，row[y] 记录了行 y 上最左和最右建筑的 x 坐标，col[x] 记录了列 x 上最上和最下建筑的 y 坐标。

3. 判断每个建筑是否满足条件

• 再次遍历所有建筑 (x, y)：
  • 检查行条件：row[y].min < x < row[y].max 是否成立。如果成立，说明在该行上，存在比 x 小的建筑（在左边）和比 x 大的建筑（在右边）。
  • 检查列条件：col[x].min < y < col[x].max 是否成立。如果成立，说明在该列上，存在比 y 小的建筑（在上边）和比 y 大的建筑（在下边）。
  • 如果行条件和列条件同时成立，则该建筑满足“四个方向均有建筑”的条件，计数加一。

4. 返回结果

• 返回满足条件的建筑总数。

示例说明

对于输入 n=3, buildings=[[1,1],[1,2],[2,1],[2,2]]：

• 行 1：建筑 x=1 和 x=2 → min=1, max=2。
• 行 2：建筑 x=1 和 x=2 → min=1, max=2。
• 列 1：建筑 y=1 和 y=2 → min=1, max=2。
• 列 2：建筑 y=1 和 y=2 → min=1, max=2。

检查每个建筑：

• (1,1)：行 1 中 x=1 不是 min<x<max（x=1 等于 min），不满足行条件。
• (1,2)：行 2 中 x=1 等于 min，不满足行条件。
• (2,1)：行 1 中 x=2 等于 max，不满足行条件。
• (2,2)：行 2 中 x=2 等于 max，不满足行条件。

因此结果为 0。

复杂度分析

时间复杂度

• 初始化 row 和 col 数组：O(n)。
• 遍历所有建筑更新 row 和 col：O(k)，其中 k = len(buildings)。
• 再次遍历所有建筑检查条件：O(k)。
• 总时间复杂度：O(n + k)。由于 k 最多为 100000，n 最多为 100000，这是线性的，可以接受。

空间复杂度

• row 和 col 数组各需要 O(n) 空间。
• 总额外空间复杂度：O(n)。

总结：
该算法通过记录每行和每列的最小/最大坐标，高效地判断每个建筑是否在四个方向上都有其他建筑，时间复杂度 O(n+k)，空间复杂度 O(n)。

Go完整代码如下：

package main

import (
	"fmt"
	"math"
)

func countCoveredBuildings(n int, buildings [][]int) (ans int) {
	type pair struct{ min, max int }
	row := make([]pair, n+1)
	col := make([]pair, n+1)
	for i := 1; i <= n; i++ {
		row[i].min = math.MaxInt
		col[i].min = math.MaxInt
	}

	add := func(m []pair, x, y int) {
		m[y].min = min(m[y].min, x)
		m[y].max = max(m[y].max, x)
	}
	isInner := func(m []pair, x, y int) bool {
		return m[y].min < x && x < m[y].max
	}

	for _, p := range buildings {
		x, y := p[0], p[1]
		add(row, x, y) // x 加到 row[y] 中
		add(col, y, x) // y 加到 col[x] 中
	}

	for _, p := range buildings {
		x, y := p[0], p[1]
		if isInner(row, x, y) && isInner(col, y, x) {
			ans++
		}
	}
	return
}

func main() {
	n := 3
	buildings := [][]int{{1, 1}, {1, 2}, {2, 1}, {2, 2}}
	result := countCoveredBuildings(n, buildings)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

def countCoveredBuildings(n, buildings):
    class Pair:
        def __init__(self):
            self.min = float('inf')
            self.max = float('-inf')
    
    row = [Pair() for _ in range(n+1)]
    col = [Pair() for _ in range(n+1)]
    
    def add(m, x, y):
        m[y].min = min(m[y].min, x)
        m[y].max = max(m[y].max, x)
    
    def is_inner(m, x, y):
        return m[y].min < x < m[y].max
    
    for p in buildings:
        x, y = p[0], p[1]
        add(row, x, y)  # x 加到 row[y] 中
        add(col, y, x)  # y 加到 col[x] 中
    
    ans = 0
    for p in buildings:
        x, y = p[0], p[1]
        if is_inner(row, x, y) and is_inner(col, y, x):
            ans += 1
    
    return ans

def main():
    n = 3
    buildings = [[1, 1], [1, 2], [2, 1], [2, 2]]
    result = countCoveredBuildings(n, buildings)
    print(result)

if __name__ == "__main__":
    main()