2025-10-14:单位转换Ⅰ。用go语言,有 n 种度量单位,编号为 0 到 n−1。 输入一个长度为 n−1 的二维数组
2025-10-14:单位转换Ⅰ。用go语言,有 n 种度量单位,编号为 0 到 n−1。
输入一个长度为 n−1 的二维数组 conversions,每一项表示一种单位与另一种单位之间的换算关系:某个源单位等于若干个目标单位。
请你求出一个长度为 n 的数组 baseUnitConversion,其中 baseUnitConversion[i] 表示 1 个类型 0 的单位等于多少个类型 i 的单位。
由于数值可能很大,结果对 1000000007 取模后返回。
2 <= n <= 100000。
conversions.length == n - 1。
0 <= sourceUniti, targetUniti < n。
1 <= conversionFactori <= 1000000000。
保证单位 0 可以通过 唯一 的转换路径(不需要反向转换)转换为任何其他单位。
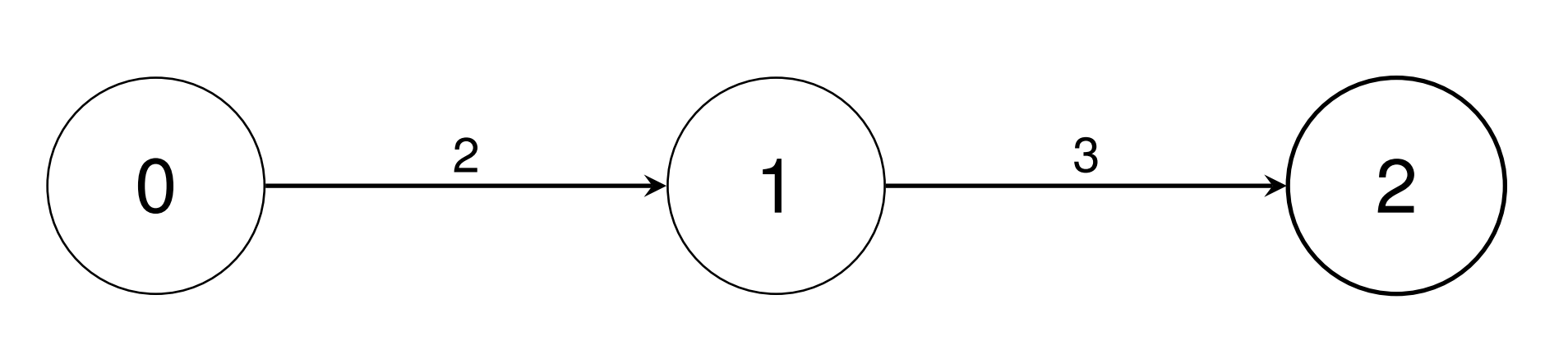
输入: conversions = [[0,1,2],[1,2,3]]。
输出: [1,2,6]。
解释:
使用 conversions[0]:将一个 0 类型单位转换为 2 个 1 类型单位。
使用 conversions[0] 和 conversions[1] 将一个 0 类型单位转换为 6 个 2 类型单位。
题目来自力扣3528。
🔄 步骤分析
-
构建有向图
程序首先需要将给出的换算关系转换成一种便于遍历的数据结构。每个换算关系[源单位, 目标单位, 换算因子]可以理解为从“源单位”节点指向“目标单位”节点的一条有向边,边的权重就是“换算因子”。这里使用邻接表来存储这个图,这是一种非常高效且节省空间的表示方法 。具体来说,会创建一个长度为n(单位数量)的切片g,其中g[x]是一个列表,存储所有从单位x出发的边(包括目标单位和换算因子)。- 例如,对于输入
conversions = [[0,1,2],[1,2,3]],构建的图如下:g[0]包含一条边:指向单位1,因子为2。g[1]包含一条边:指向单位2,因子为3。g[2]是一个空列表。
- 例如,对于输入
-
执行深度优先搜索(DFS)
已知单位0是基准单位,所以baseUnitConversion[0] = 1(1个单位0等于1个自己)。目标是计算出单位0到其他所有单位的累积换算因子。由于转换路径唯一,从单位0出发到任意单位只有一条路径,这非常适合使用深度优先搜索(DFS) 来遍历整棵树 。- 算法从一个递归的DFS函数开始,参数是当前访问的单位节点
x和从单位0到x的当前累积换算因子mul。 - 在访问节点
x时,直接将当前累积因子mul存入结果数组ans[x]。这表示1个单位0等于mul个单位x。 - 然后,递归地访问
x的所有出边指向的邻居节点(即在图中所有由单位x直接转换得到的单位)。对于每条指向邻居y且换算因子为w的边,新的累积因子是mul * w。因为从0到y的因子等于从0到x的因子(mul)乘以从x到y的因子(w)。 - 为了防止整数溢出,每次乘法运算后都对结果取模(
1_000_000_007)。
- 算法从一个递归的DFS函数开始,参数是当前访问的单位节点
-
启动遍历并返回结果
遍历从根节点(单位0)开始,初始累积因子为1。DFS会递归地访问所有与单位0连通的单位节点。当整个DFS遍历完成后,结果数组ans中就存储了所有单位相对于单位0的换算因子。
🧮 复杂度分析
-
时间复杂度:O(n)
整个算法主要包含两个部分:构建图和DFS遍历。- 构建图:需要处理
n-1条边,每条边被添加到邻接表中的操作是常数时间,所以时间复杂度是 O(n)。 - DFS遍历:每个节点仅被访问一次,每条边也被访问一次。因为图是一棵树,边数就是
n-1,所以遍历的时间复杂度也是 O(n)。 - 因此,总的时间复杂度是 O(n)。
- 构建图:需要处理
-
额外空间复杂度:O(n)
算法消耗的额外空间主要包括:- 图的邻接表 (
g):存储n个节点和n-1条边,空间复杂度为 O(n)。 - 结果数组 (
ans):长度为n,空间复杂度为 O(n)。 - DFS的递归调用栈:在最坏情况下(图退化成一条链),递归深度为
n,空间复杂度为 O(n)。 - 因此,总的额外空间复杂度是 O(n)。
- 图的邻接表 (
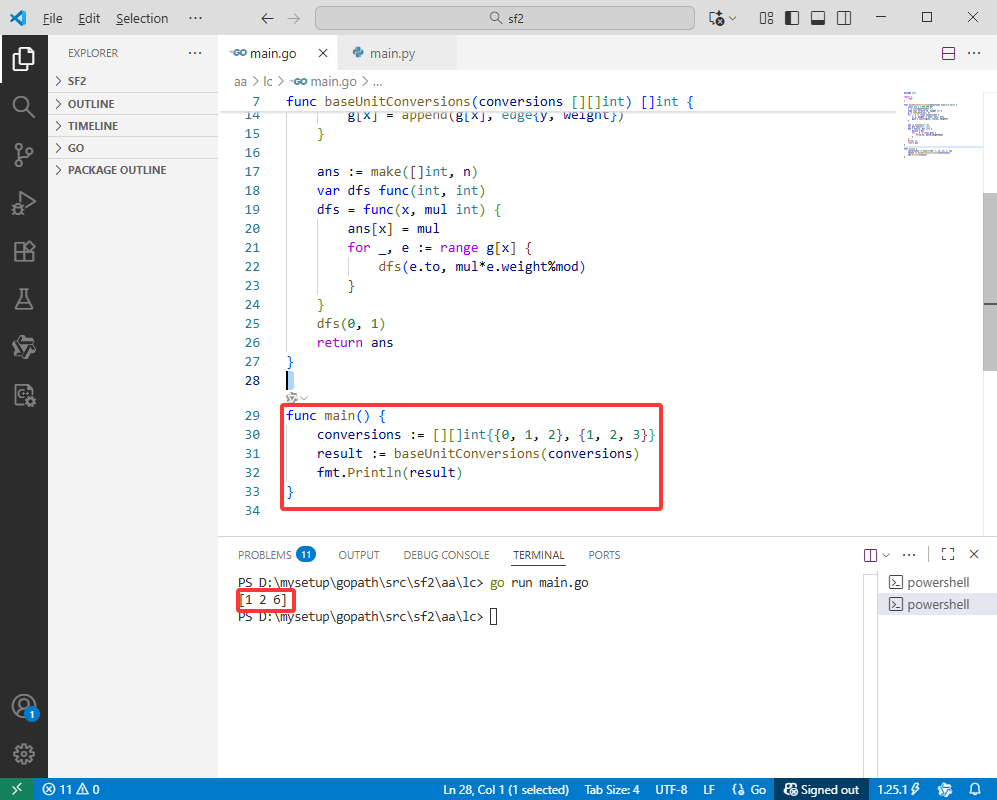
Go完整代码如下:
package main
import (
"fmt"
)
func baseUnitConversions(conversions [][]int) []int {
const mod = 1_000_000_007
n := len(conversions) + 1
type edge struct{ to, weight int }
g := make([][]edge, n)
for _, e := range conversions {
x, y, weight := e[0], e[1], e[2]
g[x] = append(g[x], edge{y, weight})
}
ans := make([]int, n)
var dfs func(int, int)
dfs = func(x, mul int) {
ans[x] = mul
for _, e := range g[x] {
dfs(e.to, mul*e.weight%mod)
}
}
dfs(0, 1)
return ans
}
func main() {
conversions := [][]int{{0, 1, 2}, {1, 2, 3}}
result := baseUnitConversions(conversions)
fmt.Println(result)
}
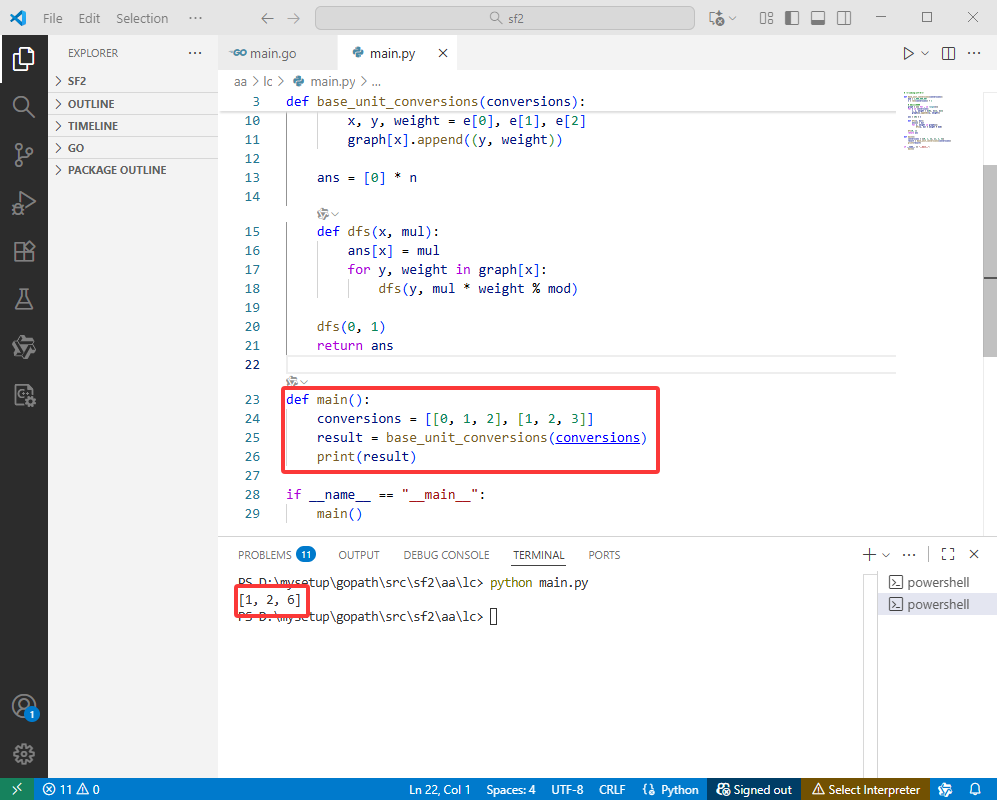
Python完整代码如下:
# -*-coding:utf-8-*-
def base_unit_conversions(conversions):
mod = 1_000_000_007
n = len(conversions) + 1
# 构建邻接表
graph = [[] for _ in range(n)]
for e in conversions:
x, y, weight = e[0], e[1], e[2]
graph[x].append((y, weight))
ans = [0] * n
def dfs(x, mul):
ans[x] = mul
for y, weight in graph[x]:
dfs(y, mul * weight % mod)
dfs(0, 1)
return ans
def main():
conversions = [[0, 1, 2], [1, 2, 3]]
result = base_unit_conversions(conversions)
print(result)
if __name__ == "__main__":
main()
- 点赞
- 收藏
- 关注作者


评论(0)