2025-10-06：最小回文排列Ⅱ。用go语言，给定一个本身就是回文的字符串 s 和一个整数 k。把 s 的字符重新排列，找出所有不同且仍然是回文的字符串，并按字典序从小到大排序。返回这个有序序列中的第 k 个字符串；如果这样的不同回文排列不足 k 个，则返回空字符串。

术语说明（便于理解）：

• 回文：从左到右读与从右到左读相同的字符串。

• 排列：对原字符串中字符位置进行重新组合得到的新字符串。

• 唯一性：不同的重排如果生成了相同的回文结果，只计为一个。

• 字典序比较：逐位比较字符，首个不同处字符较小的一侧字典序更小；若一个字符串是另一个的前缀，则更短的那个更小。

1 <= s.length <= 10000。

s 由小写英文字母组成。

保证 s 是回文字符串。

1 <= k <= 1000000。

输入： s = “abba”, k = 2。

输出： “baab”。

解释：

“abba” 的两个不同的回文排列是 “abba” 和 “baab”。

按字典序，“abba” 位于 “baab” 之前。由于 k = 2，输出为 “baab”。

题目来自力扣3518。

解决过程

1. 预处理字符频率统计

• 计算字符串长度 n 和中间位置 mid = n/2
• 创建一个长度为26的数组 counts 来统计左半部分每个字符的出现次数
• 只遍历左半部分字符（索引 0 到 mid-1），统计每个字符的频率

2. 可行性检查

• 调用 perm 函数计算左半部分所有可能的排列数量
• 如果排列数量小于 k，说明没有足够的回文排列，直接返回空字符串

3. 构造左半部分字符串

这是核心的贪心构造过程：

• 从左到右逐个位置确定字符
• 对于每个位置，按字典序从 ‘a’ 到 ‘z’ 尝试每个可能的字符：
  • 如果该字符在 counts 中还有剩余次数，暂时选择它
  • 计算选择当前字符后，剩余位置的所有排列数量：
    • 从 counts 中减少当前字符的计数
    • 调用 perm 计算剩余字符的排列数
  • 如果排列数 >= k：确定选择当前字符，继续处理下一个位置
  • 如果排列数 < k：恢复字符计数，k 减去这个排列数，尝试下一个字符

4. 构建完整回文

• 左半部分构造完成后：
  • 如果是奇数长度字符串，在中间添加原字符串中间位置的字符
  • 将左半部分反转后拼接到右侧，形成完整的回文

辅助函数说明

perm 函数

计算给定字符频率下的排列数：

• 输入：剩余位置数 total，字符频率数组 counts，阈值 k
• 计算多重集合的排列数公式：total! / (count1! × count2! × ...)
• 使用组合数相乘的方式计算，避免直接计算阶乘的溢出
• 如果中间结果超过 k，提前返回最大值（优化）

comb 函数

计算组合数 C(n, m)：

• 使用公式：C(n, m) = n×(n-1)×…×(n-m+1) / m!
• 采用迭代计算，每次乘一个数除一个数，避免大数运算
• 如果中间结果超过 k，提前返回最大值

示例分析

对于 s = "abba", k = 2：

• 左半部分字符：‘a’, ‘b’，频率：a:1, b:1
• 可能的左半部分排列：[“ab”, “ba”]
• 对应完整回文：[“abba”, “baab”]
• 第2个是 “baab”

复杂度分析

时间复杂度

• 字符频率统计：O(n)
• 可行性检查：O(26 × n) 最坏情况
• 构造过程：每个位置最多尝试26个字符，每次尝试需要计算排列数，最坏 O(26² × n)
• 总体：O(26² × n) = O(676n) ≈ O(n)（因为26是常数）

额外空间复杂度

• 字符频率数组：O(26) = O(1)
• 字符串构建器：O(n)
• 递归调用栈：O(1)（没有递归）
• 总体：O(n)（主要用于存储结果字符串）

这个算法通过贪心构造和组合数学计算，高效地找到了第k小的回文排列。

Go完整代码如下：

package main

import (
	"fmt"
	"math"
	"strings"
)

func smallestPalindrome(s string, k int) string {
	n := len(s)
	mid := n / 2
	counts := make([]int, 26)

	for i := 0; i < mid; i++ {
		c := s[i]
		counts[c-'a']++
	}

	if perm(mid, counts, k) < k {
		return ""
	}

	var sb strings.Builder
	for i := 0; i < mid; i++ {
		flag := false
		for c := 'a'; c <= 'z' && !flag; c++ {
			index := int(c - 'a')
			if counts[index] == 0 {
				continue
			}

			counts[index]--
			permutations := perm(mid-i-1, counts, k)
			if permutations >= k {
				sb.WriteByte(byte(c))
				flag = true
			} else {
				counts[index]++
				k -= permutations
			}
		}
	}

	if n%2 != 0 {
		sb.WriteByte(s[mid])
	}

	// Build the right half by reversing the left half
	leftStr := sb.String()
	sb.Reset()
	sb.WriteString(leftStr)

	// Append the reversed left half
	for i := len(leftStr) - 1; i >= 0; i-- {
		if n%2 != 0 && i == len(leftStr)-1 {
			continue // Skip the middle character in odd length case
		}
		sb.WriteByte(leftStr[i])
	}

	return sb.String()
}

func perm(total int, counts []int, k int) int {
	permutations := int64(1)
	for _, count := range counts {
		if count == 0 {
			continue
		}
		combVal := comb(total, count, k)
		if int64(combVal) > int64(k) {
			return math.MaxInt32
		}
		permutations *= int64(combVal)
		if permutations > int64(k) {
			return math.MaxInt32
		}
		total -= count
	}
	return int(permutations)
}

func comb(n, m, k int) int {
	if m > n-m {
		m = n - m
	}
	combinations := int64(1)
	for i, j := n, 1; j <= m; i, j = i-1, j+1 {
		combinations = combinations * int64(i) / int64(j)
		if combinations > int64(k) {
			return math.MaxInt32
		}
	}
	return int(combinations)
}

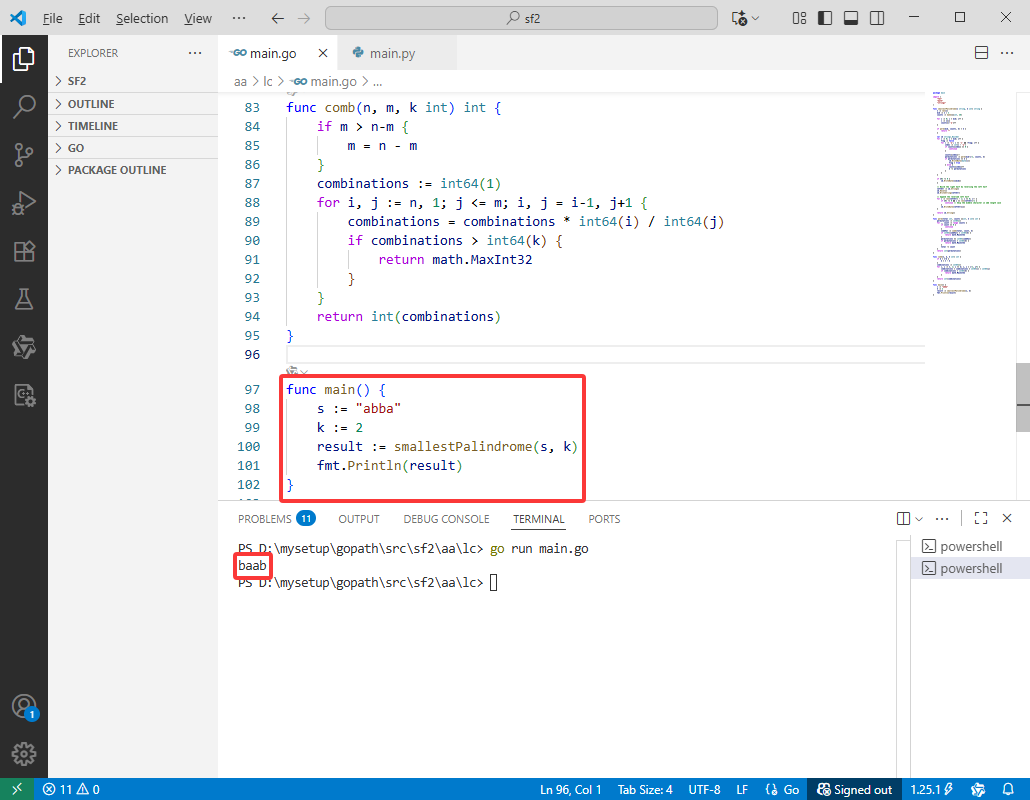
func main() {
	s := "abba"
	k := 2
	result := smallestPalindrome(s, k)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

import math

def smallestPalindrome(s: str, k: int) -> str:
    n = len(s)
    mid = n // 2
    counts = [0] * 26
    
    for i in range(mid):
        c = s[i]
        counts[ord(c) - ord('a')] += 1
    
    if perm(mid, counts, k) < k:
        return ""
    
    sb = []
    for i in range(mid):
        flag = False
        for c in range(ord('a'), ord('z') + 1):
            if flag:
                break
            index = c - ord('a')
            if counts[index] == 0:
                continue
            
            counts[index] -= 1
            permutations = perm(mid - i - 1, counts, k)
            if permutations >= k:
                sb.append(chr(c))
                flag = True
            else:
                counts[index] += 1
                k -= permutations
    
    if n % 2 != 0:
        sb.append(s[mid])
    
    # Build the complete palindrome
    left_str = ''.join(sb)
    if n % 2 != 0:
        # For odd length, the middle character is already included
        right_str = left_str[-2::-1]  # Reverse excluding the middle character
    else:
        right_str = left_str[::-1]  # Reverse the entire left half
    
    return left_str + right_str

def perm(total: int, counts: list, k: int) -> int:
    permutations = 1
    for count in counts:
        if count == 0:
            continue
        comb_val = comb(total, count, k)
        if comb_val > k:
            return math.inf
        permutations *= comb_val
        if permutations > k:
            return math.inf
        total -= count
    return permutations

def comb(n: int, m: int, k: int) -> int:
    m = min(m, n - m)
    combinations = 1
    i, j = n, 1
    while j <= m:
        combinations = combinations * i // j
        if combinations > k:
            return math.inf
        i -= 1
        j += 1
    return combinations

# Test
if __name__ == "__main__":
    s = "abba"
    k = 2
    result = smallestPalindrome(s, k)
    print(result)