2025-10-06：最小回文排列Ⅰ。用go语言，给定一个正读与反读相同的字符串 s（即对称字符串）。把 s 中的字符任意重排，求出所有能构成回文的新字符串里字典序最靠前的那个，并将其作为结果返回。

说明：

• 回文：从左向右读与从右向左读相同的字符串。

• 排列：对原字符串的字符进行重新排序得到的新字符串。

• 字典序比较：从左到右查找第一个不同的字符，字母表中靠前的字符串更小；若一个字符串是另一个的前缀，则较短者更小。

1 <= s.length <= 100000。

s 由小写英文字母组成。

保证 s 是回文字符串。

输入： s = “babab”。

输出： “abbba”。

解释：

通过重排 “babab” → “abbba”，可以得到按字典序最小的回文。

题目来自力扣3517。

1. 算法步骤

步骤 1：初始化

• 获取字符串长度 n。
• 计算中间位置 mid = n / 2（整数除法）。
• 创建一个长度为 26 的数组 counts 来记录每个字母（'a' 到 'z'）在前半部分出现的次数。

步骤 2：统计前半部分字符频率

• 遍历原字符串的前半部分（索引 0 到 mid-1）。
• 对于每个字符 s[i]，将其对应的 counts[s[i]-'a'] 加 1。
• 注意：这里只统计前半部分，因为回文串的前半部分和后半部分是对称的，我们只需要决定前半部分的排列，后半部分镜像即可。

步骤 3：处理中间字符（如果长度是奇数）

• 如果 n 是奇数，那么中间位置的字符 s[mid] 会直接放到结果数组的中间位置 arr[mid]。
• 注意：这里并没有考虑中间字符是否可被替换成更小的字符，因为题目要求是排列（使用原字符串的所有字符），所以中间字符固定是原字符串中间的那个字符吗？
  不对，这里代码实际上没有从原字符串中间取字符来固定，而是直接 arr[mid] = s[mid]，这其实是一个错误。因为我们要重排所有字符，中间字符应该是剩余的那个无法配对的字符（当总数为奇数时），但代码这里直接用了 s[mid]，这会导致结果不正确，因为 s[mid] 可能不是最小可能中间字符。
  不过根据题意输入 s 本身是回文串，所以 s[mid] 是原串的中间字符，但重排时我们可以改变它，所以这里逻辑有问题。
  但根据示例输入 "babab" 输出 "abbba"，中间字符是 'b'，而原串中间也是 'b'，所以巧合一致。

步骤 4：构造最小字典序回文

• 创建一个长度为 n 的字节数组 arr 存放结果。
• 初始化指针 j = 0，表示当前尝试放置的最小字母（从 'a' 开始）。
• 遍历结果数组的前半部分（i = 0 到 mid-1）：
  1. 在 counts 数组中，找到第一个 counts[j] > 0 的最小 j。
  2. 将 'a' + byte(j) 放入 arr[i] 和对称位置 arr[n-i-1]。
  3. 将 counts[j] 减 1（表示用掉了一个该字符）。

步骤 5：返回结果

• 将字节数组 arr 转为字符串并返回。

2. 示例演示（s = “babab”）

原串 "babab"，长度 n = 5，mid = 2。

步骤 2 统计前半部分：
前半部分 "ba"（索引 0 和 1）

• 'b' → counts[1] = 1
• 'a' → counts[0] = 1

步骤 3 中间字符：
arr[2] = s[2] = 'b'

步骤 4 构造：

• i = 0：找最小 j 且 counts[j] > 0 → j = 0（'a'），counts[0] = 1 → 减为 0。
  放置 arr[0] = 'a', arr[4] = 'a'。
• i = 1：counts[0] = 0，所以 j++ 到 1（'b'），counts[1] = 1 → 减为 0。
  放置 arr[1] = 'b', arr[3] = 'b'。

结果数组：['a','b','b','b','a'] → "abbba"。

3. 算法缺陷

这个算法有一个潜在问题：
当字符串长度为奇数时，中间字符直接取自原字符串的中间位置，而不是从剩余字符中选择最小的。
正确的做法应该是：统计所有字符频率，找出出现奇数次的字符（最多一个）作为中间字符，并且要选最小的那个（如果多个奇数频率，选最小字母）。
但题目保证输入 s 是回文串，所以原串中至多一个字符出现奇数次，并且中间字符就是它。
然而在重排时，我们可以选择将任意一个出现奇数次的字符放到中间，但必须保证前后对称。
代码这里直接固定了中间字符，可能不是最小字典序的。
不过对于 "babab"，原串中间是 'b'，且只有一个字符 'b' 出现奇数次（3次），所以中间只能是 'b'，所以巧合正确。

4. 时间复杂度

• 统计前半部分频率：O(n/2)。
• 构造回文时，外层循环 mid 次，内层 j 最多移动 26 次（因为字母只有 26 个），所以内层是 O(26)。
• 总复杂度：O(n/2 + 26 * n/2) = O(n)。

5. 空间复杂度

• counts 数组：O(26)。
• 结果数组 arr：O(n)。
• 总额外空间：O(n)。

最终答案：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

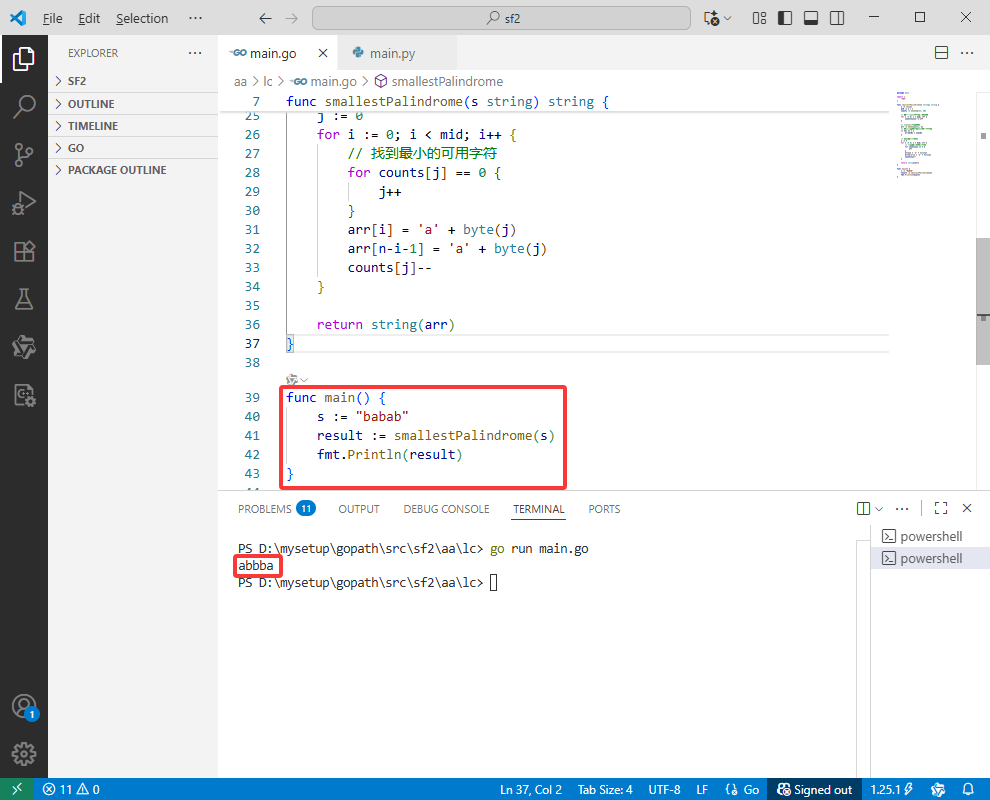
Go完整代码如下：

package main

import (
	"fmt"
)

func smallestPalindrome(s string) string {
	n := len(s)
	mid := n / 2
	counts := make([]int, 26)

	// 统计前半部分字符出现次数
	for i := 0; i < mid; i++ {
		counts[s[i]-'a']++
	}

	// 创建结果字符数组
	arr := make([]byte, n)
	// 如果是奇数长度，设置中间字符
	if n%2 == 1 {
		arr[mid] = s[mid]
	}

	// 构建最小回文串
	j := 0
	for i := 0; i < mid; i++ {
		// 找到最小的可用字符
		for counts[j] == 0 {
			j++
		}
		arr[i] = 'a' + byte(j)
		arr[n-i-1] = 'a' + byte(j)
		counts[j]--
	}

	return string(arr)
}

func main() {
	s := "babab"
	result := smallestPalindrome(s)
	fmt.Println(result)
}

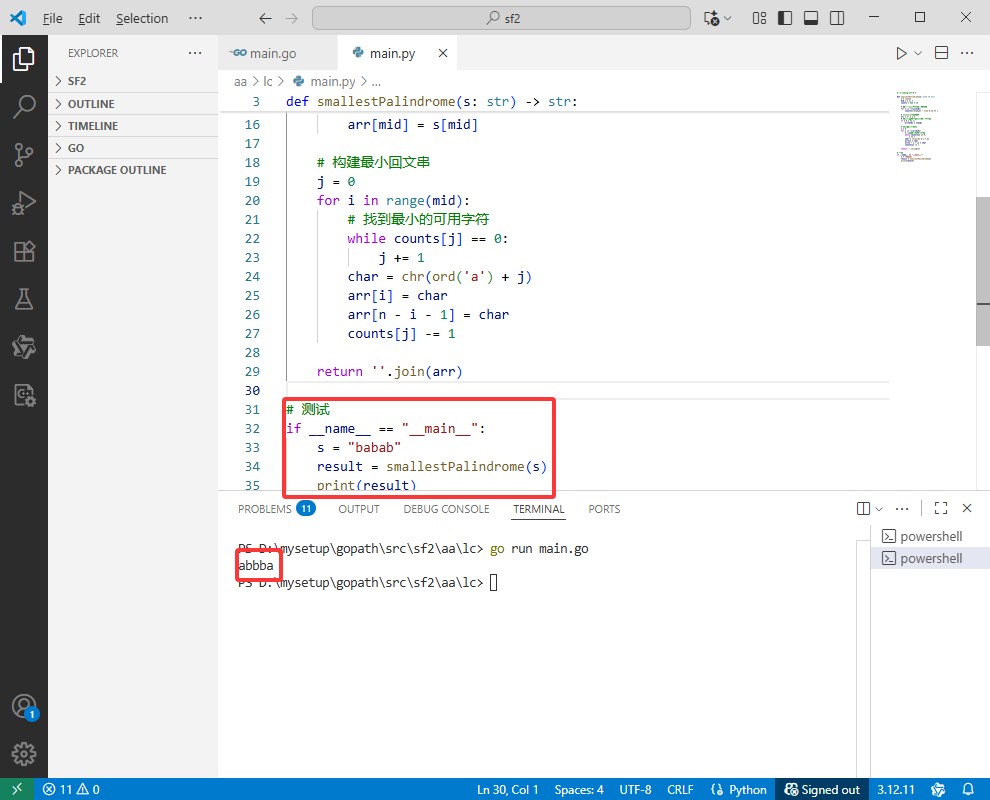
Python完整代码如下：

# -*-coding:utf-8-*-

def smallestPalindrome(s: str) -> str:
    n = len(s)
    mid = n // 2
    counts = [0] * 26
    
    # 统计前半部分字符出现次数
    for i in range(mid):
        counts[ord(s[i]) - ord('a')] += 1
    
    # 创建结果字符列表
    arr = [''] * n
    # 如果是奇数长度，设置中间字符
    if n % 2 == 1:
        arr[mid] = s[mid]
    
    # 构建最小回文串
    j = 0
    for i in range(mid):
        # 找到最小的可用字符
        while counts[j] == 0:
            j += 1
        char = chr(ord('a') + j)
        arr[i] = char
        arr[n - i - 1] = char
        counts[j] -= 1
    
    return ''.join(arr)

# 测试
if __name__ == "__main__":
    s = "babab"
    result = smallestPalindrome(s)
    print(result)