2025-07-28:最长特殊路径。用go语言,你有一棵无向树,节点编号从0到n-1,根节点是0。树的结构由一个长度为n-1的二
2025-07-28:最长特殊路径。用go语言,你有一棵无向树,节点编号从0到n-1,根节点是0。树的结构由一个长度为n-1的二维数组edges给出,其中每个元素edges[i] = [ui, vi, lengthi]表示节点ui和节点vi之间有一条边,边的长度为lengthi。同时,有一个整型数组nums,其中nums[i]代表节点i对应的数值。
定义“特殊路径”为:沿着树中从祖先节点到其后代节点的路径,该路径上所有经过的节点的值都不相同。这个路径可以是单个节点,即起点和终点相同。
现在需要你返回一个包含两个元素的数组result:
-
result[0]表示所有特殊路径中长度最长的路径的长度;
-
result[1]表示在所有最长特殊路径中,节点数量最少的那个路径的节点数目。
换句话说,就是找出树中满足节点值互异且自上而下的路径中,最长的路径长度,以及这样的最长路径中节点数目最少是多少。
2 <= n <= 5 * 10000。
edges.length == n - 1。
edges[i].length == 3。
0 <= ui, vi < n。
1 <= lengthi <= 1000。
nums.length == n。
0 <= nums[i] <= 5 * 10000。
输入保证 edges 表示一棵合法的树。
输入:edges = [[0,1,2],[1,2,3],[1,3,5],[1,4,4],[2,5,6]], nums = [2,1,2,1,3,1]。
输出:[6,2]。
解释:
下图中,nums 所代表节点的值用对应颜色表示。
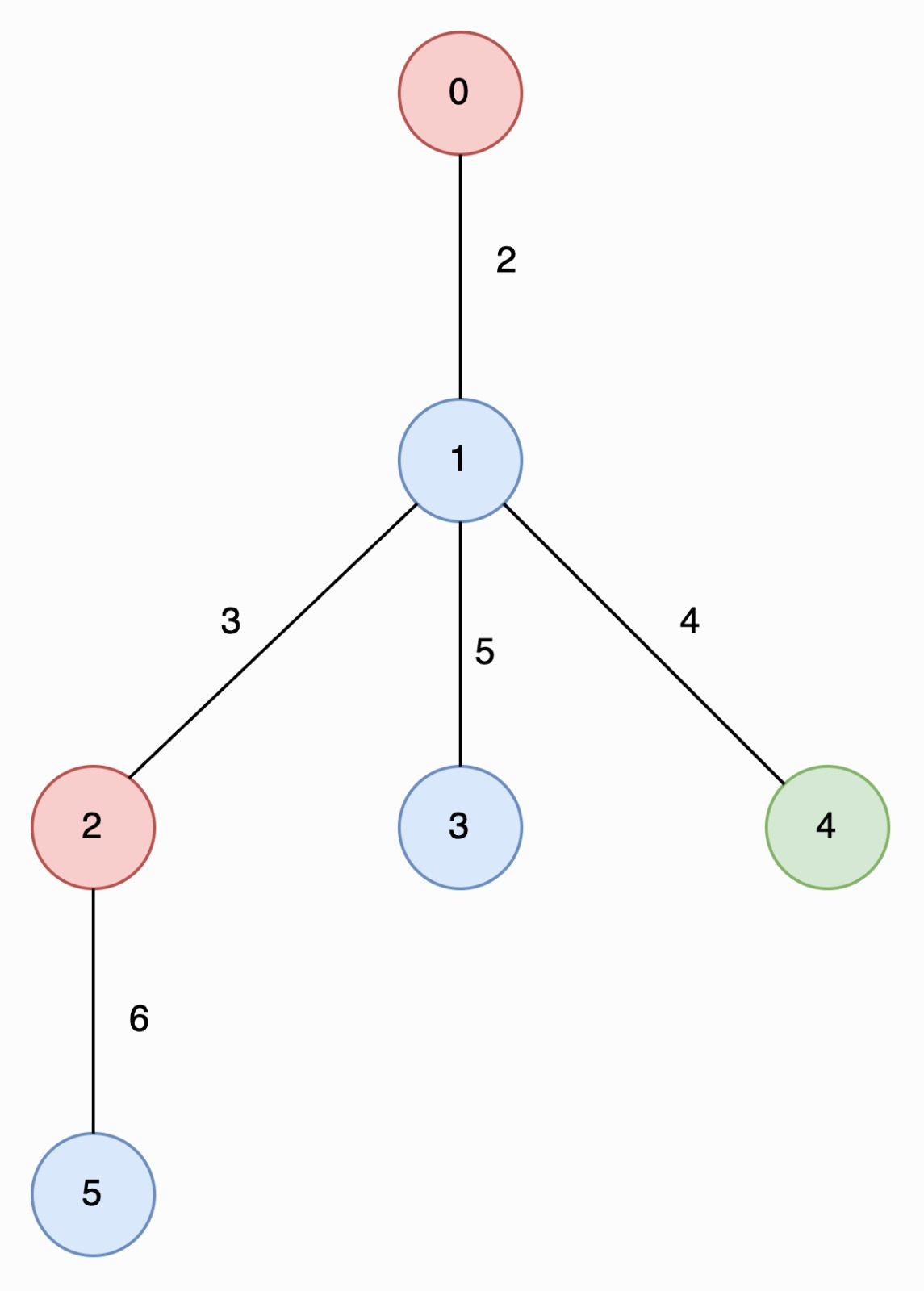
最长特殊路径为 2 -> 5 和 0 -> 1 -> 4 ,两条路径的长度都为 6 。所有特殊路径里,节点数最少的路径含有 2 个节点。
题目来自力扣3425。
代码详细执行流程(分步骤)
1. 构建图结构
- 输入 edges 和 nums。
- 用邻接表存储树结构,类型为
[][]edge,其中edge包含目标节点to及边权weight。 - 遍历 edges,将每条无向边存入两个端点的邻接表。
2. 初始化全局变量
maxLen:记录当前发现的最长路径长度,初始为 -1(因为权重全为正)。minNodes:记录在所有最长路径中,路径节点数最少的值。dis:维护当前遍历路径的累计距离,栈结构,dis[0]=0代表根节点深度 0 的距离。lastDepth:一个 map,key 为节点值(颜色),value 记录该值最后一次出现的深度索引(+1的偏移,防止默认值冲突)。
3. 定义递归 DFS 函数
-
参数:
- 当前节点
x。 - 父节点
fa,防止回溯访问父节点形成回路。 topDepth,当前特殊路径的起始节点深度,用来判断与颜色重复情况。
- 当前节点
-
DFS 步骤:
a. 取当前节点的颜色
color = nums[x]。b. 从
lastDepth中取出该颜色的上一次出现深度oldDepth。c. 更新路径“起点深度”
topDepth = max(topDepth, oldDepth),保证当前路径上不出现重复颜色(如果出现颜色重复,更新topDepth表示当前特殊路径起始点后移)。d. 计算当前路径长度:
length = dis[len(dis)-1] - dis[topDepth](利用dis维护的距离差)。e. 计算当前路径节点数:
nodes = len(dis) - topDepth。f. 若当前路径长度
length大于maxLen,更新maxLen = length,并更新minNodes = nodes。g. 若路径长度等于
maxLen,且当前节点数nodes少于minNodes,则更新minNodes = nodes。h. 将当前节点颜色出现在当前深度
len(dis),更新lastDepth[color] = len(dis)。i. 遍历所有邻居节点
y,排除父节点fa:- 将边权加到
dis中(dis = append(dis, dis[len(dis)-1]+edge.weight))。 - 递归调用 DFS。
- 恢复
dis回退。
j. 恢复当前颜色状态,即
lastDepth[color] = oldDepth,确保同色节点在不同分支的独立性。 - 将边权加到
4. 开始 DFS
- 从根节点 0 出发,以
fa = -1和初始topDepth = 0调用 DFS。
5. DFS 遍历完成
- 返回
[maxLen, minNodes]。
代码中关键技巧点及思路
- 利用
lastDepth记录颜色最后一次出现的位置深度,避免当前路径上的颜色重复,从而确定特殊路径的“起点”。 dis维护路径权重和的前缀和,通过差值直接获得任意区间路径长度。- 通过 DFS 遍历整棵树,尝试每条以祖先到后代的路径。
- 路径长度和节点数的更新条件确保符合题目最优路径要求。
- 额外注意恢复现场(路径距离和颜色深度),保证 DFS 状态正确。
时间复杂度分析
- 图中有 n 个节点,n-1 条边。
- DFS 遍历每个节点和每条边只访问一次,复杂度是 O(n)。
lastDepthmap 访问和更新操作均为 O(1)(基于哈希)。- 流程中无重复计算,保存距离的前缀和使用切片操作均摊 O(1)。
- 故总时间复杂度为 O(n)。
空间复杂度分析
- 存储邻接表需要 O(n) 空间。
- 数组
nums使用 O(n)。 - 递归栈深度最坏 O(n)。
dis最多储存树深度,最坏 O(n)。lastDepthmap 中颜色键最多为 n(节点个数),使用 O(n)。- 总空间复杂度为 O(n)。
总结
| 方面 | 复杂度 |
|---|---|
| 时间复杂度 | O(n) |
| 额外空间复杂度 | O(n) |
该算法对大规模树结构(节点数可达 5 万)也具有良好的性能。
Go完整代码如下:
package main
import (
"fmt"
)
func longestSpecialPath(edges [][]int, nums []int) []int {
type edge struct{ to, weight int }
g := make([][]edge, len(nums))
for _, e := range edges {
x, y, w := e[0], e[1], e[2]
g[x] = append(g[x], edge{y, w})
g[y] = append(g[y], edge{x, w})
}
maxLen := -1
minNodes := 0
dis := []int{0}
// 颜色 -> 该颜色最近一次出现的深度 +1,注意这里已经 +1 了
lastDepth := map[int]int{}
var dfs func(int, int, int)
dfs = func(x, fa, topDepth int) {
color := nums[x]
oldDepth := lastDepth[color]
topDepth = max(topDepth, oldDepth)
length := dis[len(dis)-1] - dis[topDepth]
nodes := len(dis) - topDepth
if length > maxLen || length == maxLen && nodes < minNodes {
maxLen = length
minNodes = nodes
}
lastDepth[color] = len(dis)
for _, e := range g[x] {
y := e.to
if y != fa { // 避免访问父节点
dis = append(dis, dis[len(dis)-1]+e.weight)
dfs(y, x, topDepth)
dis = dis[:len(dis)-1] // 恢复现场
}
}
lastDepth[color] = oldDepth // 恢复现场
}
dfs(0, -1, 0)
return []int{maxLen, minNodes}
}
func main() {
edges := [][]int{{0, 1, 2}, {1, 2, 3}, {1, 3, 5}, {1, 4, 4}, {2, 5, 6}}
nums := []int{2, 1, 2, 1, 3, 1}
result := longestSpecialPath(edges, nums)
fmt.Println(result)
}
Python完整代码如下:
# -*-coding:utf-8-*-
from typing import List
def longestSpecialPath(edges: List[List[int]], nums: List[int]) -> List[int]:
n = len(nums)
g = [[] for _ in range(n)]
for x, y, w in edges:
g[x].append((y, w))
g[y].append((x, w))
maxLen = -1
minNodes = 0
dis = [0]
lastDepth = {}
def dfs(x: int, fa: int, topDepth: int):
nonlocal maxLen, minNodes
color = nums[x]
oldDepth = lastDepth.get(color, 0)
topDepth = max(topDepth, oldDepth)
length = dis[-1] - dis[topDepth]
nodes = len(dis) - topDepth
if length > maxLen or (length == maxLen and nodes < minNodes):
maxLen = length
minNodes = nodes
lastDepth[color] = len(dis)
for y, w in g[x]:
if y != fa:
dis.append(dis[-1] + w)
dfs(y, x, topDepth)
dis.pop()
if oldDepth == 0:
lastDepth.pop(color, None)
else:
lastDepth[color] = oldDepth
dfs(0, -1, 0)
return [maxLen, minNodes]
# 测试
edges = [[0, 1, 2], [1, 2, 3], [1, 3, 5], [1, 4, 4], [2, 5, 6]]
nums = [2, 1, 2, 1, 3, 1]
result = longestSpecialPath(edges, nums)
print(result)
- 点赞
- 收藏
- 关注作者


评论(0)