2025-07-27：将数组变相同的最小代价。用go语言，你有两个长度均为 n 的整型数组 arr 和 brr，还有一个整数 k。你可以对 arr 进行以下两种操作，次数不限：

1. 将 arr 分成若干连续的子数组，然后按照任意顺序重新排列，这个操作的代价是 k。

2. 选择 arr 中的任意一个元素，并将该元素增加或减少一个正整数 x，代价为 x。

请你计算并返回将 arr 变成 brr 所需的最小总代价。

说明：子数组指数组中一段连续且非空的元素序列。

1 <= arr.length == brr.length <= 100000。

0 <= k <= 2 * 10000000000。

-100000 <= arr[i] <= 100000。

-100000<= brr[i] <= 100000。

输入：arr = [-7,9,5], brr = [7,-2,-5], k = 2。

输出：13。

解释：

将 arr 分割成两个连续子数组：[-7] 和 [9, 5] 然后将它们重新排列成 [9, 5, -7] ，代价为 2 。

将 arr[0] 减小 2 ，数组变为 [7, 5, -7] ，操作代价为 2 。

将 arr[1] 减小 7 ，数组变为 [7, -2, -7] ，操作代价为 7 。

将 arr[2] 增加 2 ，数组变为 [7, -2, -5] ，操作代价为 2 。

将两个数组变相等的总代价为 2 + 2 + 7 + 2 = 13 。

题目来自力扣3424。

大体步骤如下：

1. 计算不进行子数组重排操作时的代价（r1）

• 直接计算将 arr 中每个元素变为对应的 brr 元素所需的操作代价，即对每个 i，计算 |arr[i] - brr[i]|。
• 将所有差的绝对值相加，得到总代价 r1。
• 这里的意思是，没有使用操作1，即没有重排子数组，仅通过增减元素的值来变换。

2. 计算进行一次重排操作后的代价（r2）

• 对两个数组分别进行排序。排序的目的是将两个数组的元素尽量一一对应，减少单元素调整代价。
• 将 arr 和 brr 都排序后，逐一计算排序后数组对应元素的差值的绝对值之和。
• 再加上一次进行子数组重排操作的代价 k。
• 这里的思路是：尽管重排代价较大，但排序后每个元素差距减小，整体调整代价可能更低。

3. 比较两种方案，选取代价最小的

• 比较不重排情况下的代价 r1 和重排一次情况下的代价 r2。
• 返回较小者作为结果，表示最小所需总代价。

核心思路解析（用题目示例解释）

• 原始 arr = [-7, 9, 5]，brr = [7, -2, -5]， k = 2。
• 直接对应调整差价代价大：| -7-7 | + |9+2| + |5+5| = 14 + 11 + 10 = 35 （其实代码算的r1不是35，是更精确的,看上面代码和题目描述，r1 = sum of abs(arr[i] - brr[i])）
• 对两个数组排序后：
  • arr排序后: [-7, 5, 9]
  • brr排序后: [-5, -2, 7]
• 调整代价为：| -7+5 | + |5+2| + |9-7| = 2 + 7 + 2 = 11 + k = 2，得到13
• 13比不重排调整代价低，最终选择带一次重排的方案。

总结步骤（详细）

1. 直接一步步调整：

   • 遍历数组索引 i。
   • 计算 arr[i] 调整到 brr[i] 的代价为 abs(arr[i] - brr[i])。
   • 累加所有 i 的代价，得到 r1。

2. 尝试子数组重新排列操作：

   • 对 arr 进行从小到大排序。
   • 对 brr 进行从小到大排序。
   • 遍历 i，计算排序后的 arr[i] 调整到 brr[i] 的代价。
   • 将所有差值代价相加，再加上子数组重新排列操作代价 k，得到 r2。

3. 取最小代价：

   • 比较 r1 和 r2，选择较小值作为最小总代价。

复杂度分析

• 时间复杂度：

  • 计算差值代价是 O(n)。
  • 对两个数组排序的时间复杂度是 O(n log n)。
  • 所以总时间复杂度是 O(n log n)。

• 空间复杂度：

  • 排序通常在原数组上进行，不申请额外大数组。
  • 代码中只使用了固定的辅助变量。
  • 所以空间复杂度为 O(1) 或考虑语言排序算法额外栈空间，最坏也为 O(log n)。

Go完整代码如下：

package main

import (
	"fmt"
	"sort"
)

func minCost(arr []int, brr []int, k int64) int64 {
	var r1 int64 = 0
	var r2 int64 = k
	n := len(arr)

	for i := 0; i < n; i++ {
		r1 += int64(abs(arr[i] - brr[i]))
	}

	// 对 arr 和 brr 排序后计算
	sort.Ints(arr)
	sort.Ints(brr)
	for i := 0; i < n; i++ {
		r2 += int64(abs(arr[i] - brr[i]))
	}

	if r1 < r2 {
		return r1
	}
	return r2
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

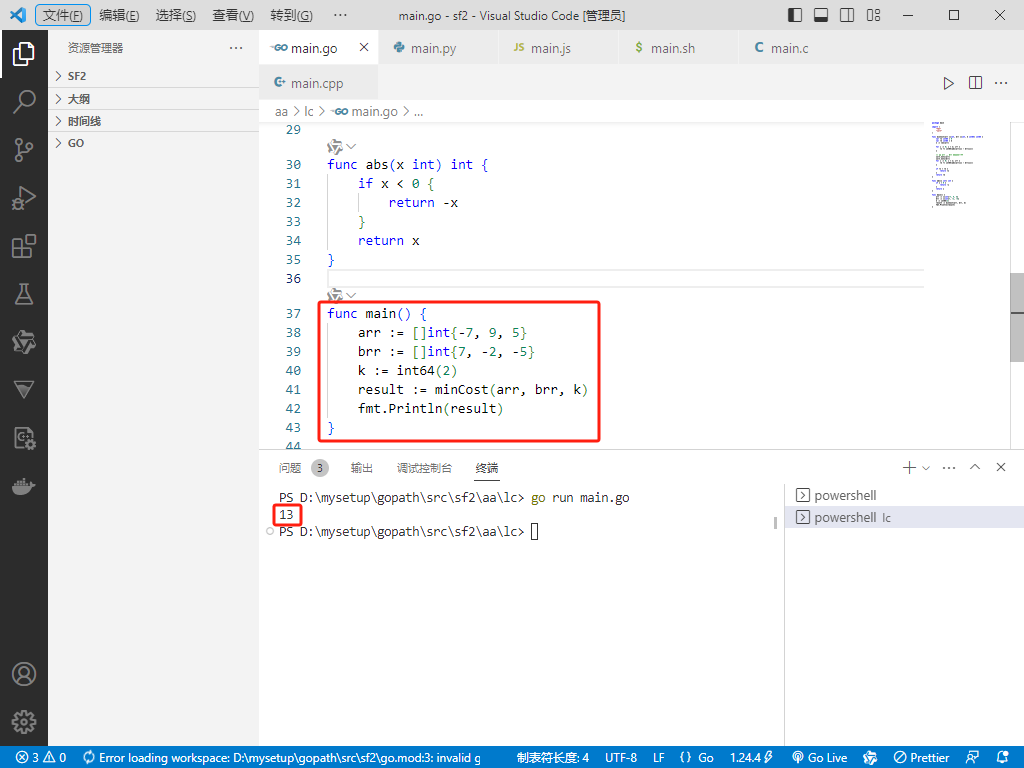
func main() {
	arr := []int{-7, 9, 5}
	brr := []int{7, -2, -5}
	k := int64(2)
	result := minCost(arr, brr, k)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

def min_cost(arr, brr, k):
    r1 = 0
    r2 = k
    n = len(arr)

    for i in range(n):
        r1 += abs(arr[i] - brr[i])

    arr_sorted = sorted(arr)
    brr_sorted = sorted(brr)
    for i in range(n):
        r2 += abs(arr_sorted[i] - brr_sorted[i])

    return min(r1, r2)


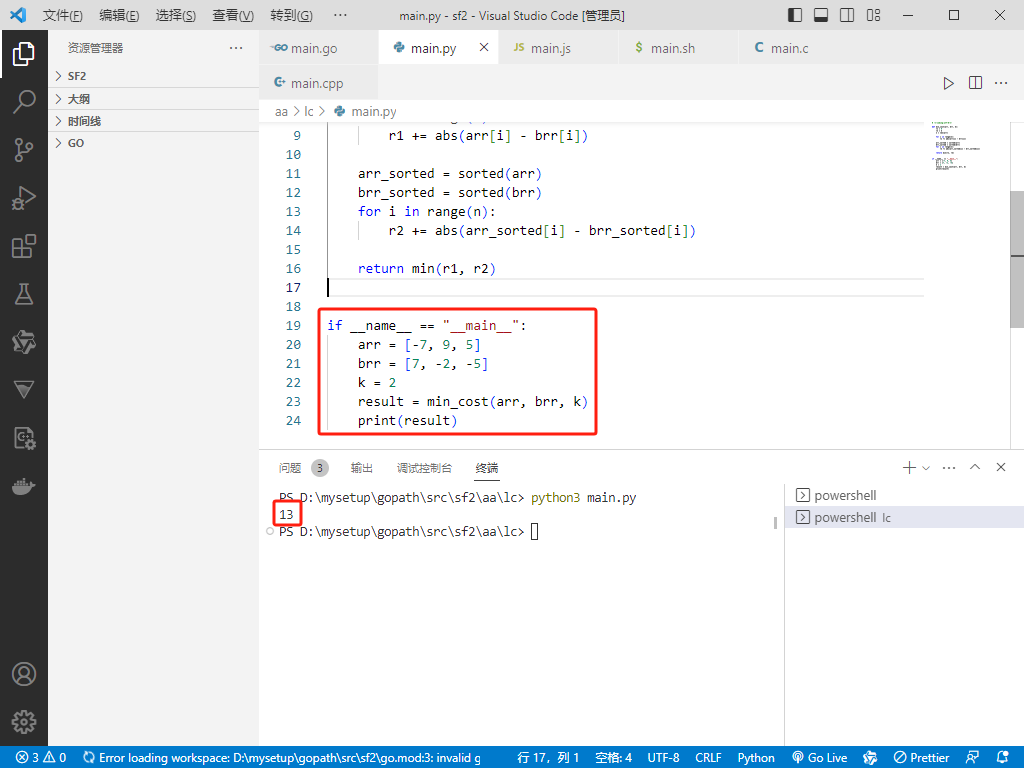
if __name__ == "__main__":
    arr = [-7, 9, 5]
    brr = [7, -2, -5]
    k = 2
    result = min_cost(arr, brr, k)
    print(result)