2025-07-24：图的最大边权的最小值。用go语言，你有一个包含 n 个节点（编号 0 到 n-1）的有向带权图，图中边的信息用二维数组 edges 表示，其中 edges[i] = [Ai, Bi, Wi] 意味着存在一条从节点 Ai 到节点 Bi 的边，权重为 Wi。

现在的任务是删除部分边（也可以不删）使得满足以下要求：

1. 图中除了节点 0 外，所有其他节点都能通过剩余的边到达节点 0。

2. 剩余边中最大的边权尽可能地小。

3. 每个节点的出边数量最多为 threshold 条。

你需要返回满足以上条件时，剩余边中最大边权的最小可能值；如果无法满足，则返回 -1。

2 <= n <= 100000。

1 <= threshold <= n - 1。

1 <= edges.length <= min(105, n * (n - 1) / 2)。

edges[i].length == 3。

0 <= Ai, Bi < n。

Ai != Bi。

1 <= Wi <= 1000000。

一对节点之间 可能 会有多条边，但它们的权值互不相同。

输入：n = 5, edges = [[1,0,1],[2,0,2],[3,0,1],[4,3,1],[2,1,1]], threshold = 2。

输出：1。

解释：

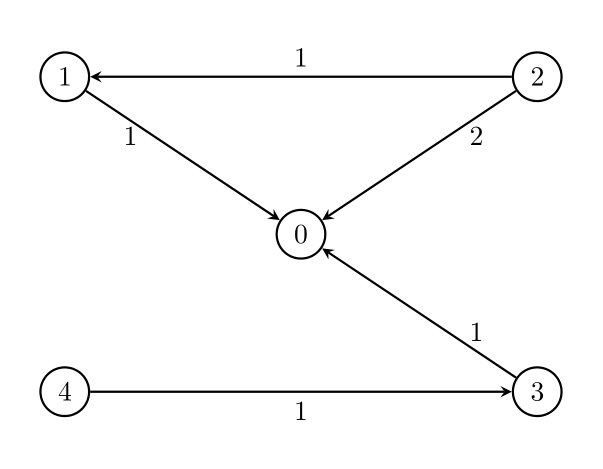
删除边 2 -> 0 。剩余边中的最大值为 1 。

题目来自力扣3419。

示例分析

输入：

• n = 5
• edges = [[1,0,1],[2,0,2],[3,0,1],[4,3,1],[2,1,1]]
• threshold = 2

初始图：

• 1 -> 0 (w=1)
• 2 -> 0 (w=2)
• 3 -> 0 (w=1)
• 4 -> 3 (w=1)
• 2 -> 1 (w=1)

目标是让所有节点（1, 2, 3, 4）都能到达 0，且每个节点的出边不超过 2，同时最大边权尽可能小。

解决思路

1. 反向图构建：为了便于计算从其他节点到 0 的路径，可以将原图反向。即，将边 Ai -> Bi 转换为 Bi -> Ai。这样，问题转化为从 0 出发是否能到达所有其他节点（即“反向可达性”）。

   • 反向图：
     • 0 -> 1 (w=1)
     • 0 -> 2 (w=2)
     • 0 -> 3 (w=1)
     • 3 -> 4 (w=1)
     • 1 -> 2 (w=1)

2. Dijkstra 算法的变种：我们需要找到从 0 到其他所有节点的路径，使得路径上的最大边权尽可能小。这与 Dijkstra 算法类似，但传统的 Dijkstra 是求最短路径（边权和最小），而这里是求路径上的最大边权最小。

   • 使用优先队列（最小堆），存储 (当前路径的最大边权, 节点)。
   • 初始化时，0 的最大边权为 0，其他节点为 ∞。
   • 每次从堆中取出最大边权最小的节点，松弛其邻边。

3. 出度限制：每个节点的出边数量不能超过 threshold。因此，在反向图中，我们需要确保每个节点的“入边”数量（即原图中的出边数量）不超过 threshold。

   • 在反向图中，Ai 的“出边”对应原图中 Ai 的“入边”，因此不需要限制。
   • 实际上，反向图中“出边”的限制需要对应原图中“入边”的限制，但题目限制的是原图中的“出边”数量。因此需要更复杂的处理。
   • 可能需要动态限制每个节点在原图中的出边数量。

4. 边选择策略：

   • 对于每个节点，选择 threshold 条最小的边，以确保最大边权最小。
   • 在反向图中，从 0 出发，优先选择较小的边，以确保路径的最大边权最小。

具体步骤

1. 构建反向图：

   • 将原图的边反向，得到反向图 g。g[y] 包含所有从 y 出发的边 (x, w)，对应原图中的 x -> y 的边 w。

2. Dijkstra 变种：

   • 初始化距离数组 dis，dis[0] = 0，其他为 ∞。
   • 使用最小堆，按路径的最大边权排序。
   • 从 0 开始，遍历邻边 (x, w)，更新 dis[x] 为 max(dis[y], w) 的最小值。

3. 出度限制：

   • 在原图中，限制每个节点的出边数量不超过 threshold。
   • 在反向图中，这对应于限制每个节点的“入边”数量。但反向图的“出边”对应原图的“入边”，因此需要确保原图的“出边”数量不超过 threshold。
   • 可能需要为每个节点维护一个“出边”列表，并选择最小的 threshold 条边。

4. 验证可达性：

   • 检查 dis 数组，确保所有节点都有有限的最大边权（即可达）。
   • 如果存在 dis[x] == ∞，则返回 -1。

5. 计算最大边权：

   • 返回 dis 数组中的最大值。

示例的具体执行

反向图：

• 0: [(1,1), (2,2), (3,1)]
• 1: [(2,1)]
• 3: [(4,1)]
• 2: []
• 4: []

Dijkstra 过程：

1. 初始堆：[(0, 0)]，dis = [0, ∞, ∞, ∞, ∞]。
2. 弹出 (0, 0)，松弛邻边：
   • (1,1)：dis[1] = max(0,1)=1，堆：[(1,1)]。
   • (2,2)：dis[2] = max(0,2)=2，堆：[(1,1), (2,2)]。
   • (3,1)：dis[3] = max(0,1)=1，堆：[(1,1), (1,3), (2,2)]。
3. 弹出 (1,1)，松弛邻边 (2,1)：
   • dis[2] = max(1,1)=1（比之前的 2 更优），堆：[(1,3), (1,2), (2,2)]。
4. 弹出 (1,3)，松弛邻边 (4,1)：
   • dis[4] = max(1,1)=1，堆：[(1,2), (1,4), (2,2)]。
5. 弹出 (1,2)，无邻边。
6. 弹出 (1,4)，无邻边。
7. 弹出 (2,2)，无邻边。

最终 dis = [0, 1, 1, 1, 1]，最大值为 1。

出度限制的处理

在原图中：

• 节点 0：出边 []（不需要限制）。
• 节点 1：出边 [0]（数量 1 <= 2）。
• 节点 2：出边 [0, 1]（数量 2 <= 2）。
• 节点 3：出边 [0, 4]（数量 2 <= 2）。
• 节点 4：出边 []（数量 0 <= 2）。

满足出度限制。

时间复杂度

1. 构建反向图：O(E)，其中 E 是边的数量。
2. Dijkstra 变种：
   • 每个节点和边最多被处理一次。
   • 堆操作的时间复杂度为 O(E log V)，其中 V 是节点数量。
3. 出度限制：
   • 可能需要为每个节点排序邻边，最坏 O(E log E)。
   • 但通常可以合并到 Dijkstra 的过程中。

总时间复杂度：O(E log V)。

空间复杂度

1. 反向图：O(E)。
2. 距离数组：O(V)。
3. 堆：O(V)。

总空间复杂度：O(E + V)。

总结

1. 构建反向图。
2. 使用 Dijkstra 变种计算从 0 到其他节点的路径的最大边权的最小值。
3. 确保原图中每个节点的出边数量不超过 threshold。
4. 检查所有节点是否可达，返回最大边权的最小值或 -1。

时间：O(E log V)，空间：O(E + V)。

Go完整代码如下：

package main

import (
	"container/heap"
	"fmt"
	"math"
	"slices"
)

func minMaxWeight(n int, edges [][]int, _ int) int {
	if len(edges) < n-1 {
		return -1
	}

	type edge struct{ to, w int }
	g := make([][]edge, n)
	for _, e := range edges {
		x, y, w := e[0], e[1], e[2]
		g[y] = append(g[y], edge{x, w})
	}

	dis := make([]int, n)
	for i := range dis {
		dis[i] = math.MaxInt
	}
	dis[0] = 0
	h := hp{{}}
	for len(h) > 0 {
		p := heap.Pop(&h).(pair)
		x := p.x
		d := p.dis
		if d > dis[x] {
			continue
		}
		for _, e := range g[x] {
			y := e.to
			newD := max(d, e.w)
			if newD < dis[y] {
				dis[y] = newD
				heap.Push(&h, pair{newD, y})
			}
		}
	}

	ans := slices.Max(dis)
	if ans == math.MaxInt {
		return -1
	}
	return ans
}

type pair struct{ dis, x int } // 路径最大边权, 节点编号
type hp []pair

func (h hp) Len() int           { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].dis < h[j].dis }
func (h hp) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v any)        { *h = append(*h, v.(pair)) }
func (h *hp) Pop() (v any)      { a := *h; *h, v = a[:len(a)-1], a[len(a)-1]; return }

func main() {
	n := 5
	edges := [][]int{{1, 0, 1}, {2, 0, 2}, {3, 0, 1}, {4, 3, 1}, {2, 1, 1}}
	threshold := 2
	result := minMaxWeight(n, edges, threshold)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

import heapq
import math

def min_max_weight(n, edges, threshold):
    # 边数量不足以连接所有节点，直接返回 -1
    if len(edges) < n - 1:
        return -1

    # 建立反向图：因为要求所有节点能到达0，方便从0开始跑反向边
    g = [[] for _ in range(n)]
    for x, y, w in edges:
        g[y].append((x, w))

    # 距离数组，dis[i]表示从节点0到i路径上边权最大值的最小可能值
    dis = [math.inf] * n
    dis[0] = 0

    # 优先队列，存放(pair(当前路径最大边权，节点))
    h = [(0, 0)]

    while h:
        cur_max, x = heapq.heappop(h)
        if cur_max > dis[x]:
            continue
        for y, w in g[x]:
            # 到节点y路径中的最大边权 = 当前路径最大边权和w的最大值
            new_max = max(cur_max, w)
            if new_max < dis[y]:
                dis[y] = new_max
                heapq.heappush(h, (new_max, y))

    ans = max(dis)
    if ans == math.inf:
        return -1
    return ans


if __name__ == "__main__":
    n = 5
    edges = [[1, 0, 1], [2, 0, 2], [3, 0, 1], [4, 3, 1], [2, 1, 1]]
    threshold = 2
    result = min_max_weight(n, edges, threshold)
    print(result)