2025-07-18：最长乘积等价子数组。用go语言，给定一个只包含正整数的数组 nums。
定义：如果一个数组 arr 满足所有元素的乘积等于该数组最大公约数（GCD）与最小公倍数（LCM）的乘积，即

prod(arr) = gcd(arr) * lcm(arr)，

则称该数组为“乘积等价数组”。

请你找出 nums 中最长的满足上述条件的连续子数组的长度。

2 <= nums.length <= 100。

1 <= nums[i] <= 10。

输入： nums = [1,2,1,2,1,1,1]。

输出： 5。

解释：

最长的乘积等价子数组是 [1, 2, 1, 1, 1]，其中 prod([1, 2, 1, 1, 1]) = 2， gcd([1, 2, 1, 1, 1]) = 1，以及 lcm([1, 2, 1, 1, 1]) = 2。

题目来自力扣3411。

分步骤描述过程

给定代码的目标是找出最长的连续子数组，满足子数组所有元素的乘积等于该子数组的最大公约数（GCD）与最小公倍数（LCM）的乘积。数组元素均为正整数，且长度在 2 到 100 之间，元素值在 1 到 10 之间。

1. 初始化：

   • ans 初始化为 2，因为任意长度为 2 的子数组都满足条件（两数恒等式：(a \times b = \text{GCD}(a,b) \times \text{LCM}(a,b))），且题目要求最长长度至少为 2。
   • mul 初始化为 1，表示当前窗口内元素的乘积（初始为空窗口）。
   • left 初始化为 0，表示滑动窗口的左边界。

2. 滑动窗口遍历（右指针 right 从 0 开始遍历数组）：

   • 当前元素处理：取 nums[right] 作为当前元素 x。
   • 窗口调整（内层循环）：
     • 计算当前乘积 mul 与 x 的最大公约数（GCD）。
     • 如果 gcd(mul, x) > 1，表示 x 与窗口内某元素有公因子（即不互质），需要缩小窗口：
       • 将 nums[left] 从 mul 中移除（mul /= nums[left]）。
       • 左指针 left 右移一位。
       • 重复此过程，直到 gcd(mul, x) == 1（即 x 与窗口内剩余元素互质）。
   • 加入新元素：将 x 乘入 mul（mul *= x），此时窗口 [left, right] 内所有元素两两互质。
   • 更新答案：计算当前窗口长度 right - left + 1，用其更新 ans 的最大值。

3. 结果返回：

   • 遍历结束后，返回 ans 作为最长满足条件的子数组长度。

关键点说明

• 窗口性质：窗口内元素始终保持两两互质。加入新元素时，通过移除左侧元素确保新元素与窗口内所有元素互质。
• 条件满足：
  • 长度为 1 的子数组：只有元素 1 满足（(1 = \text{GCD}(1) \times \text{LCM}(1))），但代码中窗口长度至少为 2（ans 初始为 2，且单个元素 1 不会更新最大长度）。
  • 长度为 2 的子数组：任意两数均满足（恒等式），但非互质数对（如 [2,4]）会被窗口拆开，不过 ans=2 已覆盖最小长度。
  • 长度 ≥3 的子数组：必须两两互质（如 [1,2,1,1,1]），窗口会捕获此类情况。
• 溢出问题：代码使用 mul 存储乘积，当窗口较长时可能溢出（如 100 个 10 的乘积远超 int64 范围），导致 GCD 计算错误。但题目元素值小（1-10），且分析基于给定代码逻辑。

复杂度分析

• 时间复杂度：(O(n))，其中 (n) 是数组长度。
  • 外层循环遍历每个元素一次（(O(n))）。
  • 内层循环中，每个元素最多被加入和移除一次（均摊 (O(1))）。
  • GCD 计算可视为常数时间（元素值小，最大 10）。
• 额外空间复杂度：(O(1))。
  • 仅使用常数个变量（ans, mul, left, 循环变量等）。

示例执行（nums = [1,2,1,2,1,1,1]）

• 窗口变化与 ans 更新：
  • [1] → ans=max(2,1)=2
  • [1,2] → ans=2（互质，长度 2）
  • [1,2,1] → ans=3（互质）
  • 加入第 4 个元素 2：不互质，移除左侧直到窗口为 [2]（移除 1），再形成 [2,2] → 因不互质，移除第一个 2，最终窗口 [2] → 加入 2 后窗口为 [2] → ans 仍为 3。
  • 后续加入 1 形成 [2,1] → [2,1,1]（ans=3）→ [2,1,1,1]（ans=4）→ [2,1,1,1,1]（ans=5）。
• 输出 5（对应子数组 [1,2,1,1,1]，索引 2 到 6）。

最终，时间复杂度为 (O(n))，额外空间复杂度为 (O(1))。但实际应用中需处理溢出问题（如改用质因数计数）。

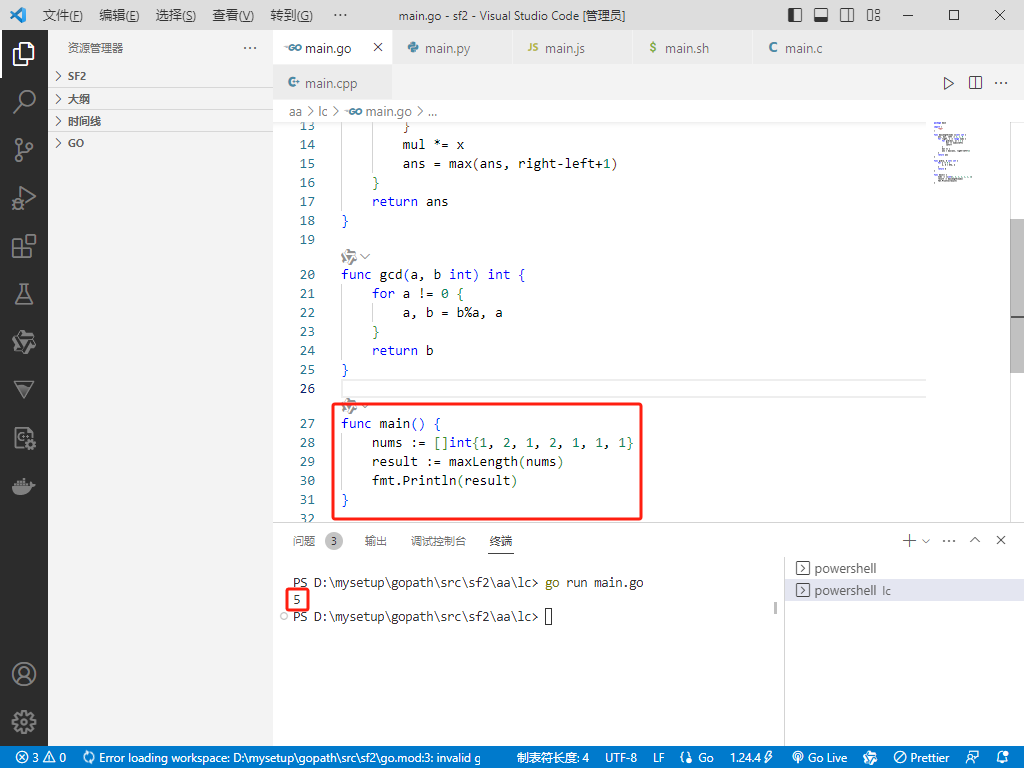
Go完整代码如下：

package main

import (
	"fmt"
)

func maxLength(nums []int) int {
	ans, mul, left := 2, 1, 0
	for right, x := range nums {
		for gcd(mul, x) > 1 {
			mul /= nums[left]
			left++
		}
		mul *= x
		ans = max(ans, right-left+1)
	}
	return ans
}

func gcd(a, b int) int {
	for a != 0 {
		a, b = b%a, a
	}
	return b
}

func main() {
	nums := []int{1, 2, 1, 2, 1, 1, 1}
	result := maxLength(nums)
	fmt.Println(result)
}

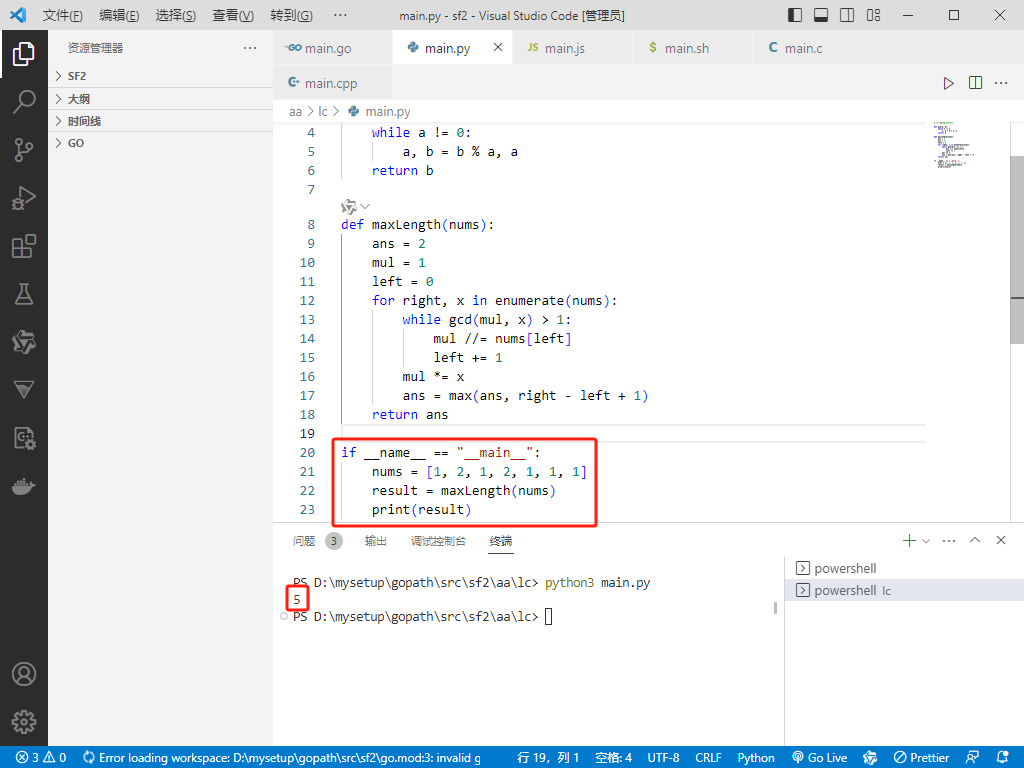
Python完整代码如下：

# -*-coding:utf-8-*-

def gcd(a, b):
    while a != 0:
        a, b = b % a, a
    return b

def maxLength(nums):
    ans = 2
    mul = 1
    left = 0
    for right, x in enumerate(nums):
        while gcd(mul, x) > 1:
            mul //= nums[left]
            left += 1
        mul *= x
        ans = max(ans, right - left + 1)
    return ans

if __name__ == "__main__":
    nums = [1, 2, 1, 2, 1, 1, 1]
    result = maxLength(nums)
    print(result)