2025-07-17：删除所有值为某个元素后的最大子数组和。用go语言，给定一个整数数组 nums，你可以进行以下操作最多一次：

• 选择数组中某个整数 X。

• 删除数组中所有值为 X 的元素，但删除后数组不能为空。

请你计算并返回，在执行上述操作后，所有可能得到的数组中的最大子数组和。

1 <= nums.length <= 100000。

-1000000 <= nums[i] <= 1000000。

输入：nums = [-3,2,-2,-1,3,-2,3]。

输出：7。

解释：

我们执行至多一次操作后可以得到以下数组：

原数组是 nums = [-3, 2, -2, -1, 3, -2, 3] 。最大子数组和为 3 + (-2) + 3 = 4 。

删除所有 X = -3 后得到 nums = [2, -2, -1, 3, -2, 3] 。最大子数组和为 3 + (-2) + 3 = 4 。

删除所有 X = -2 后得到 nums = [-3, 2, -1, 3, 3] 。最大子数组和为 2 + (-1) + 3 + 3 = 7 。

删除所有 X = -1 后得到 nums = [-3, 2, -2, 3, -2, 3] 。最大子数组和为 3 + (-2) + 3 = 4 。

删除所有 X = 3 后得到 nums = [-3, 2, -2, -1, -2] 。最大子数组和为 2 。

输出为 max(4, 4, 7, 4, 2) = 7 。

题目来自力扣3410。

示例分析

以 nums = [-3, 2, -2, -1, 3, -2, 3] 为例：

1. 不删除任何元素（原数组）：
   • 最大子数组和：3 + (-2) + 3 = 4。
2. 删除所有 X = -3：
   • 新数组：[2, -2, -1, 3, -2, 3]。
   • 最大子数组和：3 + (-2) + 3 = 4。
3. 删除所有 X = -2：
   • 新数组：[-3, 2, -1, 3, 3]。
   • 最大子数组和：2 + (-1) + 3 + 3 = 7。
4. 删除所有 X = -1：
   • 新数组：[-3, 2, -2, 3, -2, 3]。
   • 最大子数组和：3 + (-2) + 3 = 4。
5. 删除所有 X = 3：
   • 新数组：[-3, 2, -2, -1, -2]。
   • 最大子数组和：2。
     最终结果为 max(4, 4, 7, 4, 2) = 7。

解题思路

关键观察

1. 最大子数组和问题：

   • 经典的最大子数组和问题可以用 Kadane 算法 在 (O(n)) 时间内解决。
   • 但本题允许删除所有 X 后求最大子数组和，因此需要更高效的方法。

2. 删除 X 的影响：

   • 删除 X 会移除数组中所有等于 X 的元素。
   • 我们需要计算删除每个可能的 X 后的最大子数组和，并取最大值。

3. 优化思路：

   • 直接枚举所有可能的 X 并重新计算最大子数组和的时间复杂度为 (O(n^2))，对于 (n \leq 10^5) 不可行。
   • 需要一种方法在 (O(n)) 或 (O(n \log n)) 时间内解决问题。

分步过程

1. 预处理：

   • 统计所有可能的 X（即数组中所有不同的元素）。
   • 对于每个 X，记录其在数组中的位置。

2. 计算原数组的最大子数组和：

   • 用 Kadane 算法计算不删除任何元素时的最大子数组和 originalMax。

3. 计算删除每个 X 后的最大子数组和：

   • 对于每个 X，删除所有 X 后，数组会被分割成若干段。
   • 我们需要在这些段中计算最大子数组和。
   • 可以通过 前缀和 + 动态规划 的方法高效计算：
     • 维护 prefixMax 和 suffixMax 数组，分别表示从前往后和从后往前的最大子数组和。
     • 删除 X 后，数组被分割为多个不连续的段，最大子数组和可能是：
       • 某一段的内部子数组和。
       • 跨越多个段的子数组和（如果中间被删除的 X 是负数）。

4. 合并结果：

   • 对于每个 X，计算删除 X 后的最大子数组和 currentMax。
   • 最终结果为 max(originalMax, max(currentMax for all X))。

时间复杂度

1. 统计所有 X：
   • (O(n)) 时间遍历数组，用哈希表记录所有不同的 X。
2. 计算原数组的最大子数组和：
   • Kadane 算法，(O(n)) 时间。
3. 计算删除每个 X 后的最大子数组和：
   • 预处理 prefixMax 和 suffixMax 数组，(O(n)) 时间。
   • 对于每个 X，计算分割后的最大子数组和：
     • 每个 X 的处理时间为 (O(k))，其中 k 是该 X 的出现次数。
     • 所有 X 的总处理时间为 (O(n))（因为每个元素最多被处理一次）。
4. 总时间复杂度：
   • (O(n))（统计 X + Kadane + 预处理 + 处理所有 X）。

空间复杂度

1. 哈希表存储 X 的位置：
   • 最坏情况下需要 (O(n)) 空间（所有元素不同）。
2. prefixMax 和 suffixMax 数组：
   • 各需要 (O(n)) 空间。
3. 总空间复杂度：
   • (O(n))。

最终答案

• 时间复杂度：(O(n))。
• 空间复杂度：(O(n))。

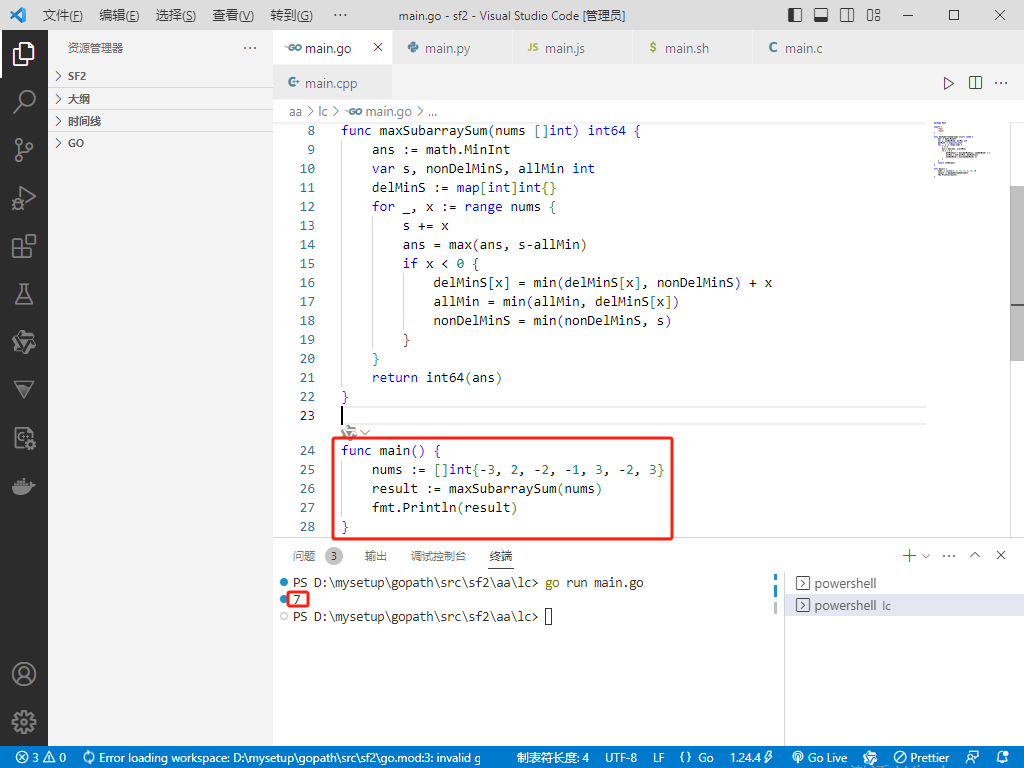
Go完整代码如下：

package main

import (
	"fmt"
	"math"
)

func maxSubarraySum(nums []int) int64 {
	ans := math.MinInt
	var s, nonDelMinS, allMin int
	delMinS := map[int]int{}
	for _, x := range nums {
		s += x
		ans = max(ans, s-allMin)
		if x < 0 {
			delMinS[x] = min(delMinS[x], nonDelMinS) + x
			allMin = min(allMin, delMinS[x])
			nonDelMinS = min(nonDelMinS, s)
		}
	}
	return int64(ans)
}

func main() {
	nums := []int{-3, 2, -2, -1, 3, -2, 3}
	result := maxSubarraySum(nums)
	fmt.Println(result)
}

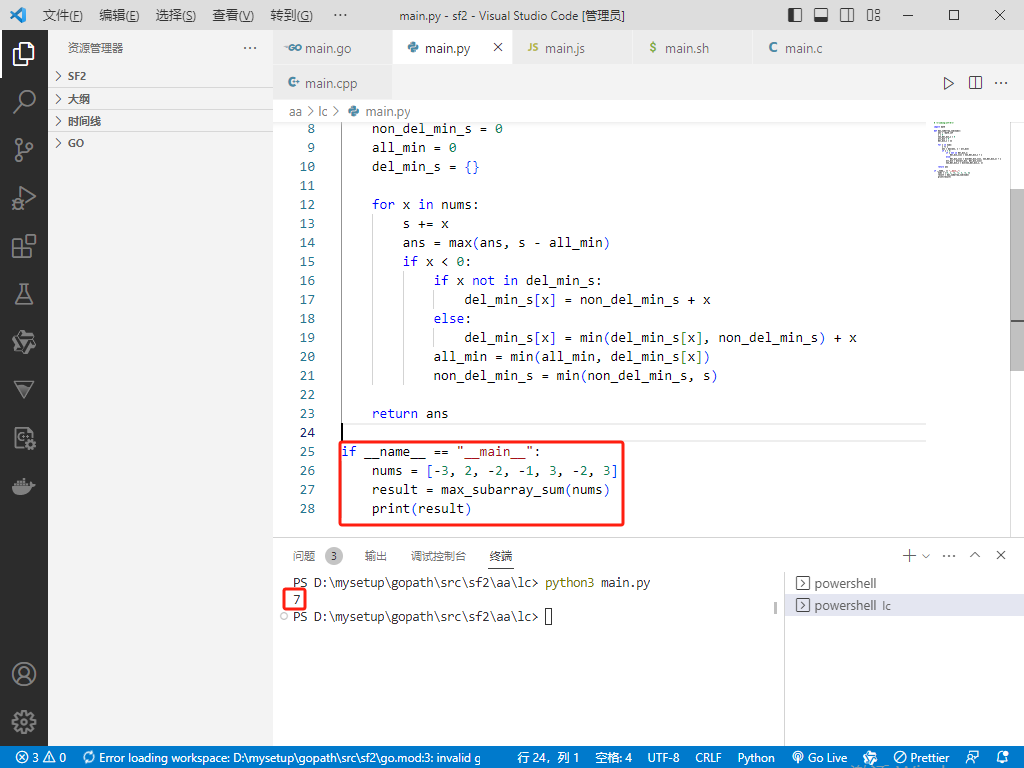
Python完整代码如下：

# -*-coding:utf-8-*-

import math

def max_subarray_sum(nums):
    ans = -math.inf
    s = 0
    non_del_min_s = 0
    all_min = 0
    del_min_s = {}

    for x in nums:
        s += x
        ans = max(ans, s - all_min)
        if x < 0:
            if x not in del_min_s:
                del_min_s[x] = non_del_min_s + x
            else:
                del_min_s[x] = min(del_min_s[x], non_del_min_s) + x
            all_min = min(all_min, del_min_s[x])
            non_del_min_s = min(non_del_min_s, s)

    return ans

if __name__ == "__main__":
    nums = [-3, 2, -2, -1, 3, -2, 3]
    result = max_subarray_sum(nums)
    print(result)