2025-07-06：判断网格图能否被切割成块。用go语言，给定一个大小为 n x n 的网格，坐标系的原点设在左下角。你有一个二维数组 rectangles，其中每个元素 rectangles[i] = [startx, starty, endx, endy] 表示一个矩形，其左下角坐标为 (startx, starty)，右上角坐标为 (endx, endy)。已知这些矩形彼此不重叠。

任务是判断是否存在两条切割线，这两条线要么都是垂直线，要么都是水平线，将网格切割成三部分。要求：

• 三部分中每一部分至少包含一个矩形；

• 每个矩形只属于其中一部分，且不会跨部分。

如果满足条件，返回 true；否则返回 false。

3 <= n <= 1000000000。

3 <= rectangles.length <= 100000。

0 <= rectangles[i][0] < rectangles[i][2] <= n。

0 <= rectangles[i][1] < rectangles[i][3] <= n。

矩形之间两两不会有重叠。

输入：n = 5, rectangles = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]]。

输出：true。

解释：

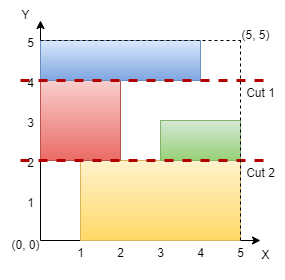
网格图如上所示，我们可以在 y = 2 和 y = 4 处进行水平切割，所以返回 true 。

题目来自力扣3394。

解决思路

1. 理解切割线的性质：

   • 如果是水平切割线，那么它们是两条水平线 y = a 和 y = b（a < b），将网格分成三部分：y < a、a ≤ y ≤ b、y > b。
   • 如果是垂直切割线，那么它们是两条垂直线 x = a 和 x = b（a < b），将网格分成三部分：x < a、a ≤ x ≤ b、x > b。
   • 需要确保所有矩形完全位于这三个部分中的一个，且每个部分至少有一个矩形。

2. 检查水平或垂直切割的可能性：

   • 分别检查是否存在两条水平线或两条垂直线满足条件。
   • 如果其中一种切割方式满足条件，则返回 true；否则返回 false。

3. 具体检查方法（以水平切割为例）：

   • 将所有矩形按照它们的垂直范围（即 y 坐标的区间 [starty, endy]）进行排序。
   • 排序后，我们需要找到两条水平线 y = a 和 y = b，使得：
     • 所有矩形的 endy ≤ a 的位于第一部分。
     • 所有矩形的 starty ≥ a 且 endy ≤ b 的位于第二部分。
     • 所有矩形的 starty ≥ b 的位于第三部分。
   • 这样，三个部分都至少有一个矩形，且没有矩形被切割线穿过（因为矩形的 y 区间是开区间，切割线不会穿过矩形）。
   • 类似地，垂直切割是检查 x 坐标的区间。

4. 具体步骤：

   • 水平切割检查：
     • 提取所有矩形的垂直区间 [starty, endy]。
     • 按照 starty 排序这些区间。
     • 遍历排序后的区间，尝试找到两个切割点 a 和 b，使得：
       • 第一部分的矩形完全在 a 下方（endy ≤ a）。
       • 第二部分的矩形完全在 a 和 b 之间（starty ≥ a 且 endy ≤ b）。
       • 第三部分的矩形完全在 b 上方（starty ≥ b）。
     • 需要确保至少有一个矩形在每一部分。
   • 垂直切割检查：
     • 类似水平切割，但检查的是 x 坐标的区间 [startx, endx]。

5. 提前终止：

   • 如果在检查水平或垂直切割时发现满足条件的情况，可以立即返回 true，无需继续检查另一种切割方式。

时间复杂度和空间复杂度

• 时间复杂度：
  • 排序矩形区间：O(m log m)，其中 m 是矩形的数量。
  • 遍历排序后的区间：O(m)。
  • 因此，总时间复杂度为 O(m log m)。
• 空间复杂度：
  • 存储矩形区间：O(m)。
  • 排序可能需要 O(log m) 的栈空间。
  • 因此，总空间复杂度为 O(m)。

总结

• 通过分别检查水平和垂直切割的可能性，可以高效解决问题。
• 主要开销在于排序矩形区间。
• 示例中水平切割 y = 2 和 y = 4 满足条件，因此返回 true。

Go完整代码如下：

package main

import (
	"fmt"
	"slices"
)

type pair struct{ l, r int }

func check(intervals []pair) bool {
	// 按照左端点从小到大排序
	slices.SortFunc(intervals, func(a, b pair) int { return a.l - b.l })
	cnt, maxR := 0, 0
	for _, p := range intervals {
		if p.l >= maxR { // 新区间
			cnt++
		}
		maxR = max(maxR, p.r) // 更新右端点最大值
	}
	return cnt >= 3 // 也可以在循环中提前退出
}

func checkValidCuts(_ int, rectangles [][]int) bool {
	a := make([]pair, len(rectangles))
	b := make([]pair, len(rectangles))
	for i, rect := range rectangles {
		a[i] = pair{rect[0], rect[2]}
		b[i] = pair{rect[1], rect[3]}
	}
	return check(a) || check(b)
}

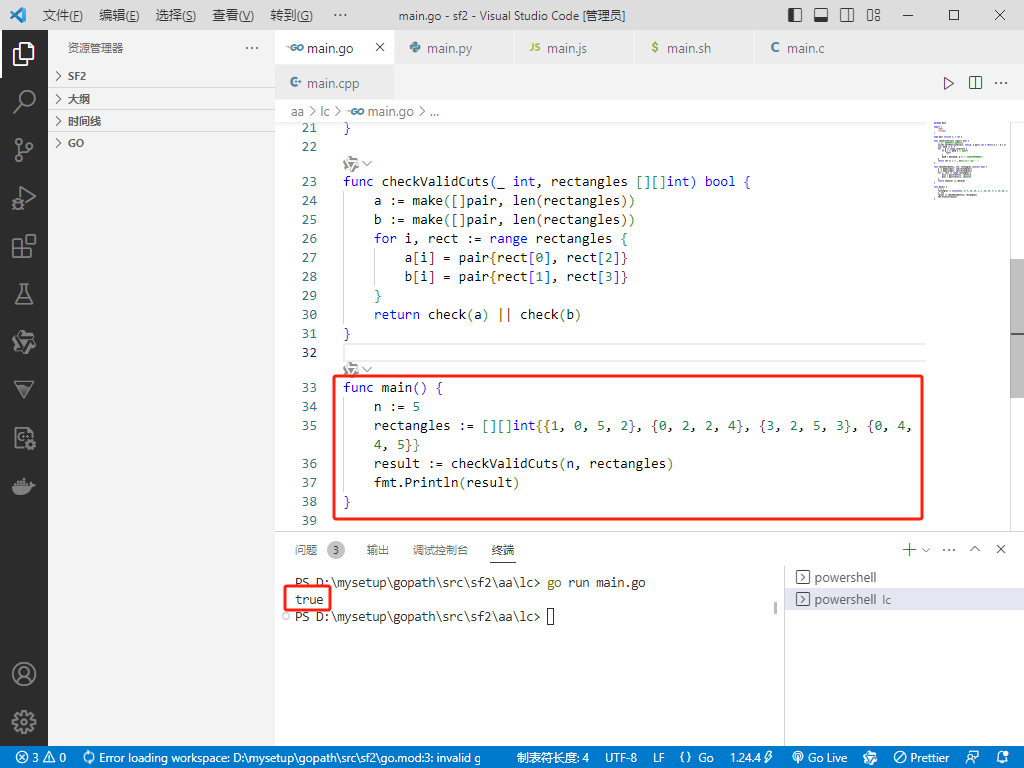
func main() {
	n := 5
	rectangles := [][]int{{1, 0, 5, 2}, {0, 2, 2, 4}, {3, 2, 5, 3}, {0, 4, 4, 5}}
	result := checkValidCuts(n, rectangles)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

from typing import List

class Pair:
    def __init__(self, l: int, r: int):
        self.l = l
        self.r = r

def check(intervals: List[Pair]) -> bool:
    # 按左端点排序
    intervals.sort(key=lambda x: x.l)
    cnt = 0
    max_r = 0
    for p in intervals:
        if p.l >= max_r:
            cnt += 1
        max_r = max(max_r, p.r)
    return cnt >= 3

def check_valid_cuts(n: int, rectangles: List[List[int]]) -> bool:
    a = [Pair(rect[0], rect[2]) for rect in rectangles]
    b = [Pair(rect[1], rect[3]) for rect in rectangles]
    return check(a) or check(b)

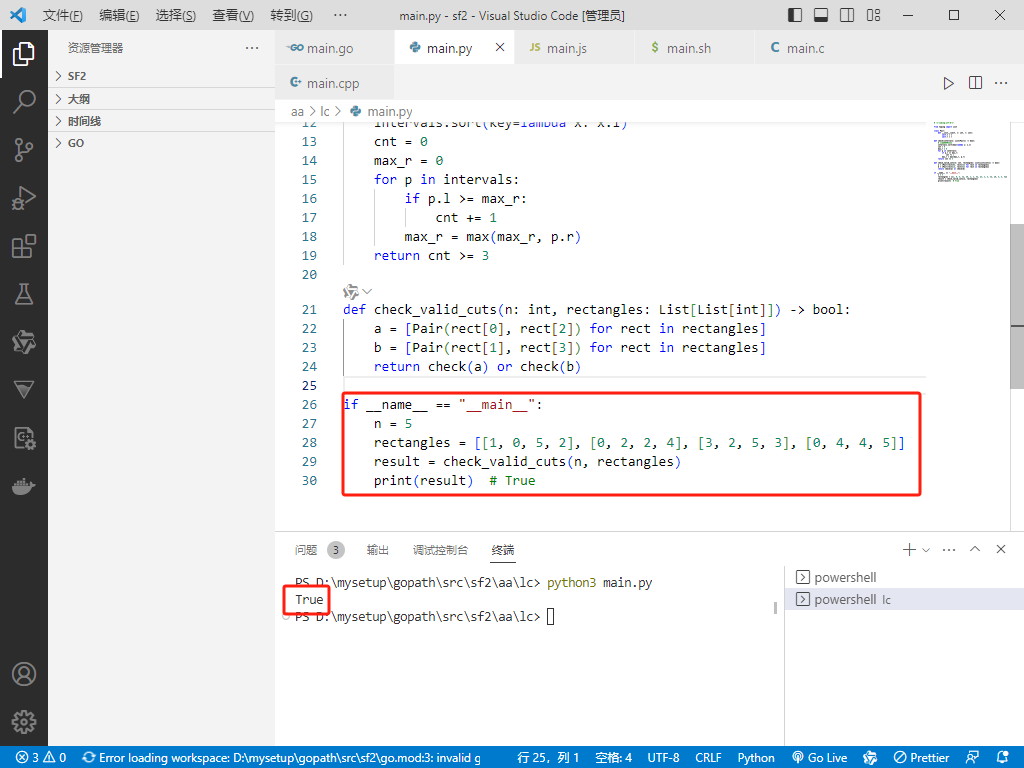
if __name__ == "__main__":
    n = 5
    rectangles = [[1, 0, 5, 2], [0, 2, 2, 4], [3, 2, 5, 3], [0, 4, 4, 5]]
    result = check_valid_cuts(n, rectangles)
    print(result)  # True