2025-06-29：用点构造面积最大的矩形Ⅱ。用go语言，在一个二维平面上有 n 个点，坐标分别由两个整数数组 xCoord 和 yCoord 给出，其中点 i 的坐标为 (xCoord[i], yCoord[i])。

需要找出一个矩形，该矩形满足以下条件：

1. 由给定点集中的四个点组成矩形的四个顶点。

2. 矩形的边与坐标轴平行。

3. 矩形内部和边界上没有其他给定点存在。

求出这样符合条件的矩形的最大面积。如果找不到符合条件的矩形，则返回 -1。

1 <= xCoord.length == yCoord.length <= 200000。

0 <= xCoord[i], yCoord[i] <= 80000000。

给定的所有点都是 唯一 的。

输入： xCoord = [1,1,3,3], yCoord = [1,3,1,3]。

输出： 4。

解释：

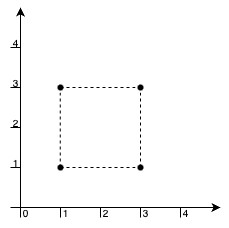
我们可以用这 4 个点作为顶点构成一个矩形，并且矩形内部或边界上没有其他点。因此，最大面积为 4 。

题目来自力扣3382。

解决思路

1. 数据预处理：

   • 首先，我们需要将所有的点按照 x 坐标和 y 坐标进行分类。可以使用两个哈希表 xMap 和 yMap，其中：
     • xMap[x] 存储所有 x 坐标为 x 的点的 y 坐标。
     • yMap[y] 存储所有 y 坐标为 y 的点的 x 坐标。
   • 然后，对 xMap 中的每个 x 对应的 y 坐标列表和 yMap 中的每个 y 对应的 x 坐标列表进行排序，以便后续快速查找相邻的点。

2. 寻找候选矩形：

   • 我们需要找到所有可能的矩形。一个矩形可以由两个 x 坐标（左边界和右边界）和两个 y 坐标（下边界和上边界）唯一确定。
   • 对于每个 x 坐标，我们检查其对应的 y 坐标列表中的相邻 y 坐标对 (y1, y2)。这意味着在 x 坐标处有两个点 (x, y1) 和 (x, y2)。
   • 对于这样的 (y1, y2) 对，我们需要检查是否存在另一个 x 坐标 x1，使得：
     • x1 是 (x, y1) 和 (x, y2) 的左侧相邻点（即 x1 是 y1 和 y2 对应的 x 坐标列表中小于 x 的最大值）。
     • 在 x1 处也存在 (x1, y1) 和 (x1, y2) 这两个点。
     • 这样，矩形的四个顶点就是 (x1, y1)、(x1, y2)、(x, y1) 和 (x, y2)。
   • 如果满足上述条件，则计算该矩形的面积，并将其作为候选矩形。

3. 验证候选矩形：

   • 对于每个候选矩形，我们需要验证其内部和边界上是否没有其他点。这可以通过二维前缀和或类似的方法来实现，但为了高效处理，可以采用以下方法：
     • 使用分治法（如 CDQ 分治）或扫描线算法来统计矩形内的点数。
     • 具体来说，对于每个候选矩形 (x1, y1, x, y2)，我们需要统计满足 x1 < x' < x 和 y1 < y' < y2 的点 (x', y') 的数量。如果数量为 0，则该矩形有效。
   • 为了高效统计，可以将所有点和查询点（矩形的四个角）一起处理，按照一定的顺序排序后，使用分治法或树状数组来统计点数。

4. 计算最大面积：

   • 遍历所有有效的候选矩形，记录其中的最大面积。如果没有有效的矩形，则返回 -1。

具体步骤

1. 构建 xMap 和 yMap：

   • 遍历所有点，将 y 坐标按 x 坐标分组，将 x 坐标按 y 坐标分组。
   • 对每个分组内的坐标进行排序。

2. 构建 below 和 left 映射：

   • below[(x, y2)] = y1：表示在 x 坐标处，y2 的下方相邻点是 y1。
   • left[(x2, y)] = x1：表示在 y 坐标处，x2 的左侧相邻点是 x1。

3. 生成候选矩形：

   • 对于每个 x 坐标及其对应的 y 坐标列表中的相邻 (y1, y2) 对：
     • 检查是否存在 x1 使得 (x1, y1) 和 (x1, y2) 都存在。
     • 如果存在，则生成候选矩形 (x1, y1, x, y2) 并计算面积。

4. 验证候选矩形：

   • 将候选矩形的四个角作为查询点，使用 CDQ 分治或类似方法统计矩形内的点数。
   • 如果点数为 0，则该矩形有效。

5. 返回结果：

   • 从所有有效矩形中选择面积最大的一个。

时间复杂度和空间复杂度

• 时间复杂度：

  • 构建 xMap 和 yMap：O(n log n)，因为需要对每个分组内的坐标排序。
  • 生成候选矩形：O(n)，因为每个点最多参与 O(1) 次矩形生成。
  • 验证候选矩形：使用 CDQ 分治的时间复杂度为 O(n log n)。
  • 总体时间复杂度：O(n log n)。

• 空间复杂度：

  • 存储 xMap 和 yMap：O(n)。
  • 存储候选矩形和查询点：O(n)。
  • 总体空间复杂度：O(n)。

Go完整代码如下：

.

package main

import (
	"fmt"
	"sort"
)

type Node struct {
	x, y int
	val  int
	idx  int
	op   int
}

func maxRectangleArea(xCoord []int, yCoord []int) int64 {
	n := len(xCoord)
	xMap := map[int][]int{}
	yMap := map[int][]int{}

	for i := 0; i < n; i++ {
		x := xCoord[i]
		y := yCoord[i]
		xMap[x] = append(xMap[x], y)
		yMap[y] = append(yMap[y], x)
	}

	// 对每个x，y坐标排序
	for x := range xMap {
		sort.Ints(xMap[x])
	}
	for y := range yMap {
		sort.Ints(yMap[y])
	}

	// below[(x,y2)] = y1 纵向相邻点，下方点y1
	below := map[[2]int]int{}
	for x, ys := range xMap {
		for i := 0; i+1 < len(ys); i++ {
			y1, y2 := ys[i], ys[i+1]
			below[[2]int{x, y2}] = y1
		}
	}
	// left[(x2,y)] = x1 横向相邻点，左侧点x1
	left := map[[2]int]int{}
	for y, xs := range yMap {
		for i := 0; i+1 < len(xs); i++ {
			x1, x2 := xs[i], xs[i+1]
			left[[2]int{x2, y}] = x1
		}
	}

	type Query struct {
		a, b, c, d int
		area       int64
	}
	queries := []Query{}

	// 找所有符合条件的矩形
	// 类似python中pairwise：遍历y的相邻配对
	for x, ys := range xMap {
		for i := 0; i+1 < len(ys); i++ {
			y1, y2 := ys[i], ys[i+1]
			x1, ok1 := left[[2]int{x, y2}]
			x1_check, ok2 := left[[2]int{x, y1}]
			if ok1 && ok2 && x1_check == x1 {
				y_below, ok3 := below[[2]int{x1, y2}]
				if ok3 && y_below == y1 {
					area := int64(y2-y1) * int64(x-x1)
					queries = append(queries, Query{a: x1, b: y1, c: x, d: y2, area: area})
				}
			}
		}
	}

	arr := []Node{}
	for i := 0; i < n; i++ {
		arr = append(arr, Node{x: xCoord[i], y: yCoord[i], val: 0, idx: 0, op: 1})
	}

	ans := make([]int, len(queries))

	for i, q := range queries {
		// 构造查询点，和差分项
		arr = append(arr, Node{x: q.c, y: q.d, val: 1, idx: i, op: 0})
		arr = append(arr, Node{x: q.a - 1, y: q.b - 1, val: 1, idx: i, op: 0})
		arr = append(arr, Node{x: q.c, y: q.b - 1, val: -1, idx: i, op: 0})
		arr = append(arr, Node{x: q.a - 1, y: q.d, val: -1, idx: i, op: 0})
	}

	sort.Slice(arr, func(i, j int) bool {
		if arr[i].x == arr[j].x {
			return arr[i].op > arr[j].op // op=1放前面，和python“-e.op”对应
		}
		return arr[i].x < arr[j].x
	})

	var merge func(l, m, r int)
	merge = func(l, m, r int) {
		j := l
		point := 0
		for i := m + 1; i <= r; i++ {
			for j <= m && arr[j].y <= arr[i].y {
				point += arr[j].op
				j++
			}
			if arr[i].op == 0 {
				ans[arr[i].idx] += arr[i].val * point
			}
		}
		// 按y排序，方便合并
		tmp := make([]Node, r-l+1)
		copy(tmp, arr[l:r+1])
		sort.Slice(tmp, func(i, j int) bool { return tmp[i].y < tmp[j].y })
		copy(arr[l:r+1], tmp)
	}

	var cdq func(l, r int)
	cdq = func(l, r int) {
		if l >= r {
			return
		}
		mid := (l + r) >> 1
		cdq(l, mid)
		cdq(mid+1, r)
		merge(l, mid, r)
	}

	cdq(0, len(arr)-1)

	res := int64(-1 << 60)
	for i := 0; i < len(queries); i++ {
		if ans[i] == 4 {
			if queries[i].area > res {
				res = queries[i].area
			}
		}
	}

	if res == int64(-1<<60) {
		return -1
	}

	return res
}

func main() {
	xCoord := []int{1, 1, 3, 3}
	yCoord := []int{1, 3, 1, 3}
	result := maxRectangleArea(xCoord, yCoord)
	fmt.Println(result)
}

Python完整代码如下：

.

# -*-coding:utf-8-*-

from typing import List, Tuple
from collections import defaultdict

class Node:
    __slots__ = ['x', 'y', 'val', 'idx', 'op']
    def __init__(self, x: int, y: int, val: int, idx: int, op: int):
        self.x = x
        self.y = y
        self.val = val
        self.idx = idx
        self.op = op

def maxRectangleArea(xCoord: List[int], yCoord: List[int]) -> int:
    n = len(xCoord)
    xMap = defaultdict(list)
    yMap = defaultdict(list)

    for i in range(n):
        x, y = xCoord[i], yCoord[i]
        xMap[x].append(y)
        yMap[y].append(x)

    for x in xMap:
        xMap[x].sort()
    for y in yMap:
        yMap[y].sort()

    below = {}
    for x, ys in xMap.items():
        for i in range(len(ys) - 1):
            y1, y2 = ys[i], ys[i+1]
            below[(x, y2)] = y1

    left = {}
    for y, xs in yMap.items():
        for i in range(len(xs) - 1):
            x1, x2 = xs[i], xs[i+1]
            left[(x2, y)] = x1

    queries = []  # type: List[Tuple[int,int,int,int,int64]]
    for x, ys in xMap.items():
        for i in range(len(ys)-1):
            y1, y2 = ys[i], ys[i+1]
            x1 = left.get((x, y2))
            x1_check = left.get((x, y1))
            if x1 is not None and x1_check == x1:
                y_below = below.get((x1, y2))
                if y_below == y1:
                    area = (y2 - y1) * (x - x1)
                    queries.append((x1, y1, x, y2, area))

    arr = [Node(xCoord[i], yCoord[i], 0, 0, 1) for i in range(n)]
    ans = [0] * len(queries)

    for i, (a, b, c, d, _) in enumerate(queries):
        arr.append(Node(c, d, 1, i, 0))
        arr.append(Node(a - 1, b - 1, 1, i, 0))
        arr.append(Node(c, b - 1, -1, i, 0))
        arr.append(Node(a - 1, d, -1, i, 0))

    # Sort the array: by x asc, if tie then op desc
    arr.sort(key=lambda e: (e.x, -e.op))

    def merge(l:int, m:int, r:int) -> None:
        j = l
        point = 0
        i_arr = arr
        tmp = i_arr[l:r+1]
        # We will do a two-pointer traverse from l to m and m+1 to r on y
        left_part = i_arr[l:m+1]
        right_part = i_arr[m+1:r+1]
        left_idx = 0
        right_idx = 0
        length_left = m - l + 1
        length_right = r - m

        # We process by walking through right_part in order of y ascending
        # But first, sort left and right parts by y ascending
        left_part.sort(key=lambda node: node.y)
        right_part.sort(key=lambda node: node.y)

        point = 0
        left_ptr = 0
        for rp in right_part:
            while left_ptr < length_left and left_part[left_ptr].y <= rp.y:
                point += left_part[left_ptr].op
                left_ptr += 1
            if rp.op == 0:
                ans[rp.idx] += rp.val * point

        # Sort back by y for arr[l:r+1]
        merged = sorted(i_arr[l:r+1], key=lambda node: node.y)
        i_arr[l:r+1] = merged

    def cdq(l:int, r:int) -> None:
        if l >= r:
            return
        mid = (l + r) >> 1
        cdq(l, mid)
        cdq(mid+1, r)
        merge(l, mid, r)

    cdq(0, len(arr)-1)

    res = -1 << 60
    for i in range(len(queries)):
        if ans[i] == 4:
            if queries[i][4] > res:
                res = queries[i][4]

    if res == -1 << 60:
        return -1
    return res

if __name__ == '__main__':
    xCoord = [1, 1, 3, 3]
    yCoord = [1, 3, 1, 3]
    result = maxRectangleArea(xCoord, yCoord)
    print(result)