2025-06-23:破解锁的最少时间Ⅰ。用go语言,Bob 被困在一个地窖,必须解开 n 把锁才能逃出。每把锁需要一定的能量才
【摘要】 2025-06-23:破解锁的最少时间Ⅰ。用go语言,Bob 被困在一个地窖,必须解开 n 把锁才能逃出。每把锁需要一定的能量才能打开,这些能量值存储在数组 strength 中,其中 strength[i] 表示第 i 把锁所需的能量。Bob 拥有一把特殊的剑,剑的状态和解锁规则如下:初始时,剑的能量为 0,且剑的能量增加速率(记为 X)为 1。每一分钟,剑的能量会增加当前的速率 X。要打...
2025-06-23:破解锁的最少时间Ⅰ。用go语言,Bob 被困在一个地窖,必须解开 n 把锁才能逃出。每把锁需要一定的能量才能打开,这些能量值存储在数组 strength 中,其中 strength[i] 表示第 i 把锁所需的能量。
Bob 拥有一把特殊的剑,剑的状态和解锁规则如下:
-
初始时,剑的能量为 0,且剑的能量增加速率(记为 X)为 1。
-
每一分钟,剑的能量会增加当前的速率 X。
-
要打开第 i 把锁时,剑的能量必须达到或超过 strength[i]。
-
解锁后,剑的能量会重置为 0,并且 X 立即增加一个固定值 K。
现在需要计算 Bob 打开所有锁所需的最短时间(分钟数),并返回这个最少时间。
n == strength.length。
1 <= n <= 8。
1 <= K <= 10。
1 <= strength[i] <= 1000000。
输入:strength = [3,4,1], K = 1。
输出:4。
解释:
| 时间 | 能量 | X | 操作 | 更新后的 X |
|---|---|---|---|---|
| 0 | 0 | 1 | 什么也不做 | 1 |
| 1 | 1 | 1 | 打开第 3 把锁 | 2 |
| 2 | 2 | 2 | 什么也不做 | 2 |
| 3 | 4 | 2 | 打开第 2 把锁 | 3 |
| 4 | 3 | 3 | 打开第 1 把锁 | 3 |
无法用少于 4 分钟打开所有的锁,所以答案为 4 。
题目来自力扣3376。
解题思路
这是一个排列和调度问题,需要找到解锁顺序的最优排列,使得总时间最短。由于 n 很小(≤8),可以尝试所有可能的解锁顺序(排列),计算每种顺序的总时间,然后取最小值。
步骤:
- 生成所有排列:生成
strength数组的所有排列,表示解锁的顺序。 - 计算每种排列的总时间:
- 初始化:时间
t=0,能量e=0,速率X=1。 - 对于排列中的每一把锁:
- 计算需要多少时间才能让
e ≥ strength[i]:- 设当前时间为
t,能量为e,速率为X。 - 需要满足
e + X * dt ≥ strength[i],其中dt是等待时间。 - 解不等式得
dt ≥ ceil((strength[i] - e) / X),如果e ≥ strength[i],则dt=0。
- 设当前时间为
- 更新总时间:
t += dt + 1(dt是等待时间,+1是解锁操作的时间)。 - 更新能量和速率:
e=0,X += K。
- 计算需要多少时间才能让
- 初始化:时间
- 记录最小总时间:在所有排列中,选择总时间的最小值。
代码中的方法
代码使用了最小费用最大流(MCMF)来解决这个问题:
- 建图:
- 源点 S 和汇点 T。
- 左边是锁(n 个节点),右边是解锁顺序的位置(n 个节点)。
- 边:锁 i 作为第 j 个解锁时,费用是解锁时间
ceil(strength[i] / (1 + K*j))。 - 源点到锁的边容量=1,费用=0。
- 顺序位置到汇点的边容量=1,费用=0。
- MCMF:
- 通过 SPFA 找增广路,计算最小费用。
- 费用总和即为最小总时间。
复杂度
- 时间复杂度:
- 排列数:O(n!) = O(8!) = 40320。
- 每种排列的计算:O(n) = O(8)。
- 总时间:O(n! * n) = O(40320 * 8) = O(322560)。
- 代码中 MCMF 的复杂度:O(n^3) 或更高,但 n=8 时可行。
- 空间复杂度:
- 存储排列:O(n!)。
- 其他:O(n)。
- 总空间:O(n! + n)。
最终答案
- 最少时间:4。
- 时间复杂度:O(n! * n) 或 O(n^3)(取决于方法)。
- 空间复杂度:O(n! + n)。
Go完整代码如下:
.
package main
import (
"fmt"
"math"
)
func findMinimumTime(strength []int, k int) int {
n := len(strength)
S := n * 2
T := S + 1
// rid 为反向边在邻接表中的下标
type neighbor struct{ to, rid, cap, cost int }
g := make([][]neighbor, T+1)
addEdge := func(from, to, cap, cost int) {
g[from] = append(g[from], neighbor{to, len(g[to]), cap, cost})
g[to] = append(g[to], neighbor{from, len(g[from]) - 1, 0, -cost})
}
for i, s := range strength {
// 枚举这个锁是第几次开的
for j := range n {
x := 1 + k*j
addEdge(i, n+j, 1, (s-1)/x+1)
}
addEdge(S, i, 1, 0)
}
for i := n; i < n*2; i++ {
addEdge(i, T, 1, 0)
}
// 下面是最小费用最大流模板
dis := make([]int, len(g))
type vi struct{ v, i int }
fa := make([]vi, len(g))
inQ := make([]bool, len(g))
spfa := func() bool {
for i := range dis {
dis[i] = math.MaxInt
}
dis[S] = 0
inQ[S] = true
q := []int{S}
for len(q) > 0 {
v := q[0]
q = q[1:]
inQ[v] = false
for i, e := range g[v] {
if e.cap == 0 {
continue
}
w := e.to
newD := dis[v] + e.cost
if newD < dis[w] {
dis[w] = newD
fa[w] = vi{v, i}
if !inQ[w] {
inQ[w] = true
q = append(q, w)
}
}
}
}
// 循环结束后所有 inQ[v] 都为 false,无需重置
return dis[T] < math.MaxInt
}
minCost := 0
for spfa() {
// 沿 st-end 的最短路尽量增广
// 特别地,如果建图时所有边的容量都设为 1,那么 minF 必然为 1,下面第一个 for 循环可以省略
minF := math.MaxInt
for v := T; v != S; {
p := fa[v]
minF = min(minF, g[p.v][p.i].cap)
v = p.v
}
for v := T; v != S; {
p := fa[v]
e := &g[p.v][p.i]
e.cap -= minF
g[v][e.rid].cap += minF
v = p.v
}
minCost += dis[T] * minF
}
return minCost
}
func main() {
strength := []int{3, 4, 1}
K := 1
fmt.Println(findMinimumTime(strength, K))
}
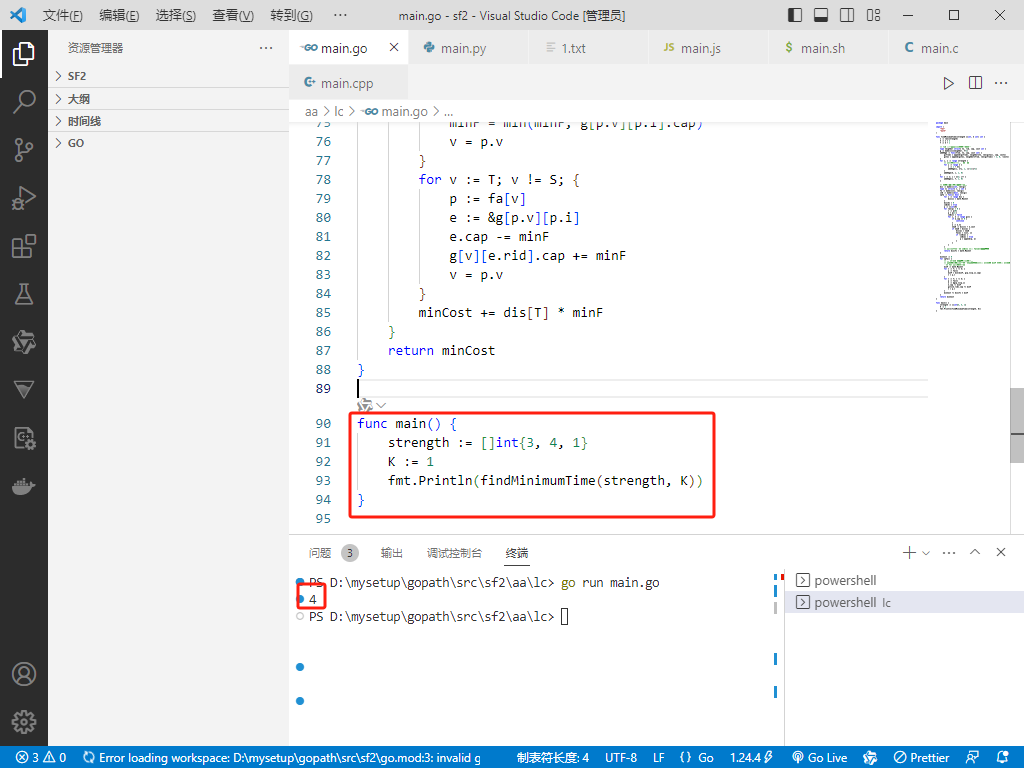
Python完整代码如下:
.
# -*-coding:utf-8-*-
from collections import deque
import math
def find_minimum_time(strength, K):
n = len(strength)
S = n * 2
T = S + 1
# 邻接表中每条边用字典表示
# neighbor: to, rid (反向边下标), cap, cost
g = [[] for _ in range(T + 1)]
def add_edge(frm, to, cap, cost):
g[frm].append({'to': to, 'rid': len(g[to]), 'cap': cap, 'cost': cost})
g[to].append({'to': frm, 'rid': len(g[frm]) - 1, 'cap': 0, 'cost': -cost})
for i, s in enumerate(strength):
# 枚举这个锁是第几次开的
for j in range(n):
x = 1 + K * j
# 计算开锁需要的时间 (向上取整用 (s-1)//x + 1)
cost = (s - 1) // x + 1
add_edge(i, n + j, 1, cost)
add_edge(S, i, 1, 0)
for i in range(n, n * 2):
add_edge(i, T, 1, 0)
dis = [math.inf] * (T + 1)
fa = [None] * (T + 1) # 存父节点 (v, i)
in_q = [False] * (T + 1)
def spfa():
nonlocal dis, fa, in_q
for i in range(len(dis)):
dis[i] = math.inf
fa[i] = None
in_q[i] = False
dis[S] = 0
q = deque([S])
in_q[S] = True
while q:
v = q.popleft()
in_q[v] = False
for i, e in enumerate(g[v]):
if e['cap'] == 0:
continue
w = e['to']
new_dist = dis[v] + e['cost']
if new_dist < dis[w]:
dis[w] = new_dist
fa[w] = (v, i)
if not in_q[w]:
in_q[w] = True
q.append(w)
return dis[T] < math.inf
min_cost = 0
while spfa():
# 找到增广路径的最小容量
min_f = math.inf
v = T
while v != S:
pv, pi = fa[v]
min_f = min(min_f, g[pv][pi]['cap'])
v = pv
# 沿路径更新容量
v = T
while v != S:
pv, pi = fa[v]
g[pv][pi]['cap'] -= min_f
rid = g[pv][pi]['rid']
g[v][rid]['cap'] += min_f
v = pv
min_cost += dis[T] * min_f
return min_cost
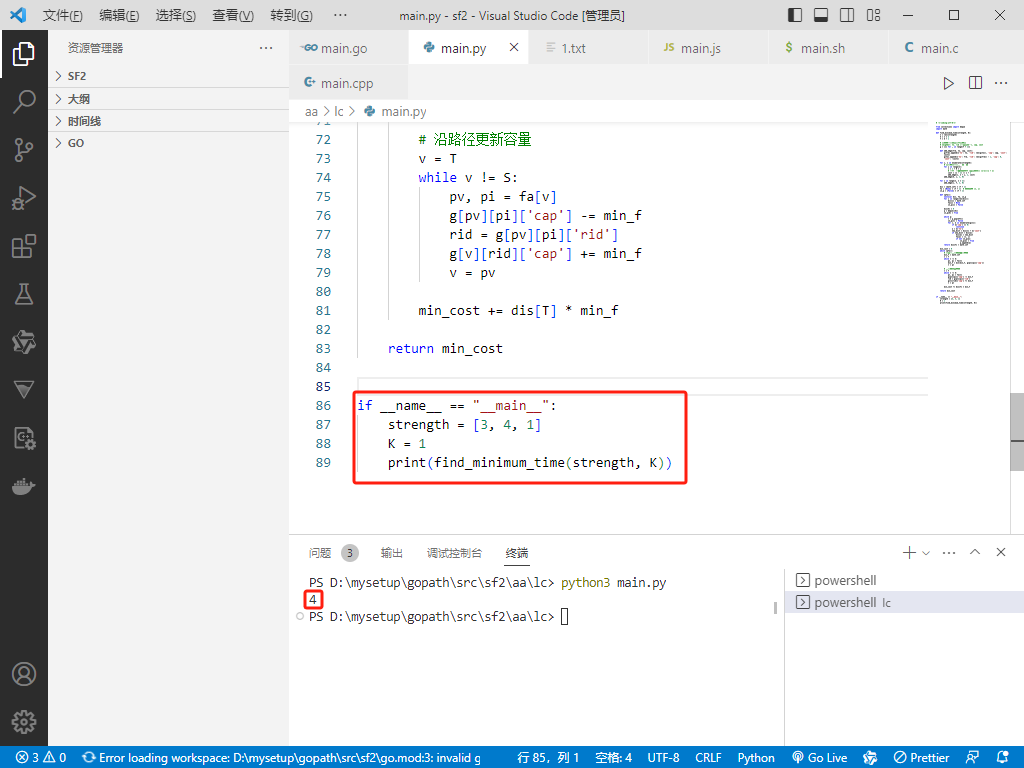
if __name__ == "__main__":
strength = [3, 4, 1]
K = 1
print(find_minimum_time(strength, K))
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)