2025-06-03：检测相邻递增子数组Ⅱ。用go语言，给定一个包含 n 个整数的数组 nums，要求找出一个最大的整数 k，使得数组中存在两个连续且长度均为 k 的子数组，它们都是严格递增的。具体要求如下：

• 找出两个子数组，分别从索引 a 和 b 开始，其中 a < b 且 b = a + k；

• 这两个子数组分别是 nums[a…a+k-1] 和 nums[b…b+k-1]；

• 两个子数组都必须满足严格递增的性质。

返回满足条件的最大 k 值。这里的子数组指的是数组中连续且非空的元素序列。

2 <= nums.length <= 2 * 100000。

-109 <= nums[i] <= 1000000000。

输入：nums = [2,5,7,8,9,2,3,4,3,1]。

输出：3。

解释：

从下标 2 开始的子数组是 [7, 8, 9]，它是严格递增的。

从下标 5 开始的子数组是 [2, 3, 4]，它也是严格递增的。

这两个子数组是相邻的，因此 3 是满足题目条件的 最大 k 值。

题目来自力扣3350。

解决思路

为了找到最大的 k，我们需要：

1. 首先找到所有可能的严格递增子数组的长度。
2. 然后检查是否存在两个相邻的严格递增子数组，其长度都至少为 k，且满足 b = a + k 的关系。
3. 最大的 k 就是满足上述条件的最大值。

具体步骤

1. 预处理严格递增子数组：

   • 遍历数组 nums，记录所有严格递增的子数组的起始和结束位置。
   • 例如，对于 nums = [2,5,7,8,9,2,3,4,3,1]，严格递增的子数组有：
     • [2,5,7,8,9]（从索引 0 到 4，长度为 5）
     • [2,3,4]（从索引 5 到 7，长度为 3）
     • [3]（从索引 8 到 8，长度为 1）
     • [1]（从索引 9 到 9，长度为 1）

2. 记录递增段的长度：

   • 将数组划分为多个严格递增的段，记录每个段的长度。
   • 对于上述示例，递增段的长度为 [5, 3, 1, 1]。

3. 寻找相邻的递增段：

   • 我们需要找到两个相邻的递增段，其中第一个段的长度至少为 k，第二个段的长度至少为 k，且 b = a + k。
   • 具体来说：
     • 对于第一个递增段 [a..a+len1-1] 和第二个递增段 [b..b+len2-1]，需要满足 b = a + k 且 len1 >= k 和 len2 >= k。
     • 因为 b 是第二个递增段的起始索引，所以 b 必须位于第一个递增段的范围内或之后。

4. 计算可能的 k：

   • 对于每一对相邻的递增段，计算可能的 k：
     • k 的最大值不能超过第一个递增段的剩余长度和第二个递增段的长度的最小值。
     • 具体来说，如果第一个递增段的长度是 len1，第二个递增段的长度是 len2，那么 k 的最大可能值是 min(len1, len2)。
   • 我们需要在所有相邻的递增段中找到最大的 k。

5. 示例的具体计算：

   • 递增段长度 [5, 3, 1, 1]：
     • 第一段长度 5，第二段长度 3：
       • k 的最大可能值是 min(5, 3) = 3。
       • 检查是否可以取 k = 3：
         • 第一段的起始索引是 0，长度为 5，所以可以取 a = 2（因为 a + k = 5，即 b = 5）。
         • 第二段的起始索引是 5，长度为 3，可以覆盖 [5..7]。
         • 因此 k = 3 是可行的。
     • 其他相邻段的 k 值较小（如 min(3, 1) = 1），因此最大 k 是 3。

时间复杂度

• 预处理严格递增子数组：需要遍历整个数组一次，时间复杂度为 O(n)。
• 计算相邻递增段的 k 值：需要遍历递增段列表一次，时间复杂度为 O(m)，其中 m 是递增段的数量（最坏情况下 m = O(n)）。
• 因此，总的时间复杂度为 O(n)。

空间复杂度

• 需要存储递增段的长度或起始结束位置，空间复杂度为 O(m)，其中 m 是递增段的数量（最坏情况下 m = O(n)）。
• 因此，总的额外空间复杂度为 O(n)。

总结

通过预处理严格递增子数组并检查相邻递增段的关系，可以在线性时间内找到最大的 k。该算法的时间复杂度为 O(n)，空间复杂度为 O(n)。

Go完整代码如下：

package main

import (
	"fmt"
)

func maxIncreasingSubarrays(nums []int) (ans int) {
	preCnt, cnt := 0, 0
	for i, x := range nums {
		cnt++
		if i == len(nums)-1 || x >= nums[i+1] { // i 是严格递增段的末尾
			ans = max(ans, cnt/2, min(preCnt, cnt))
			preCnt = cnt
			cnt = 0
		}
	}
	return
}

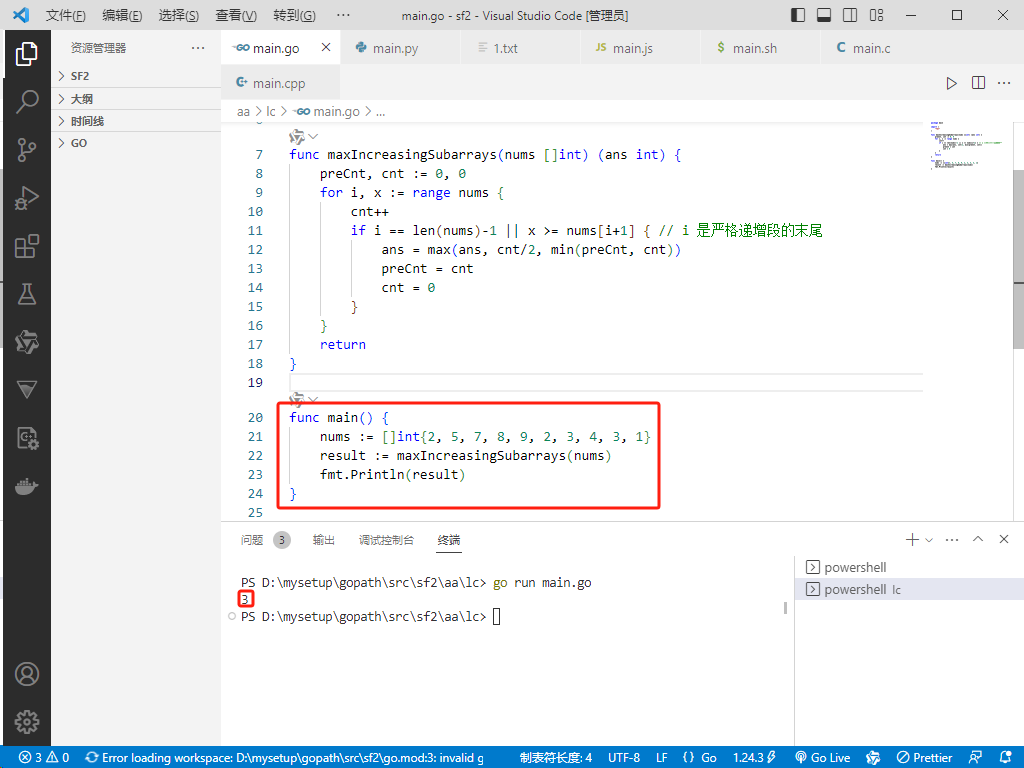
func main() {
	nums := []int{2, 5, 7, 8, 9, 2, 3, 4, 3, 1}
	result := maxIncreasingSubarrays(nums)
	fmt.Println(result)
}

Python完整代码如下：

.

# -*-coding:utf-8-*-

def max_increasing_subarrays(nums):
    def max_val(*args):
        return max(args)

    def min_val(a, b):
        return a if a < b else b

    ans = 0
    pre_cnt = 0
    cnt = 0
    n = len(nums)

    for i, x in enumerate(nums):
        cnt += 1
        if i == n - 1 or x >= nums[i + 1]:
            ans = max_val(ans, cnt // 2, min_val(pre_cnt, cnt))
            pre_cnt = cnt
            cnt = 0

    return ans


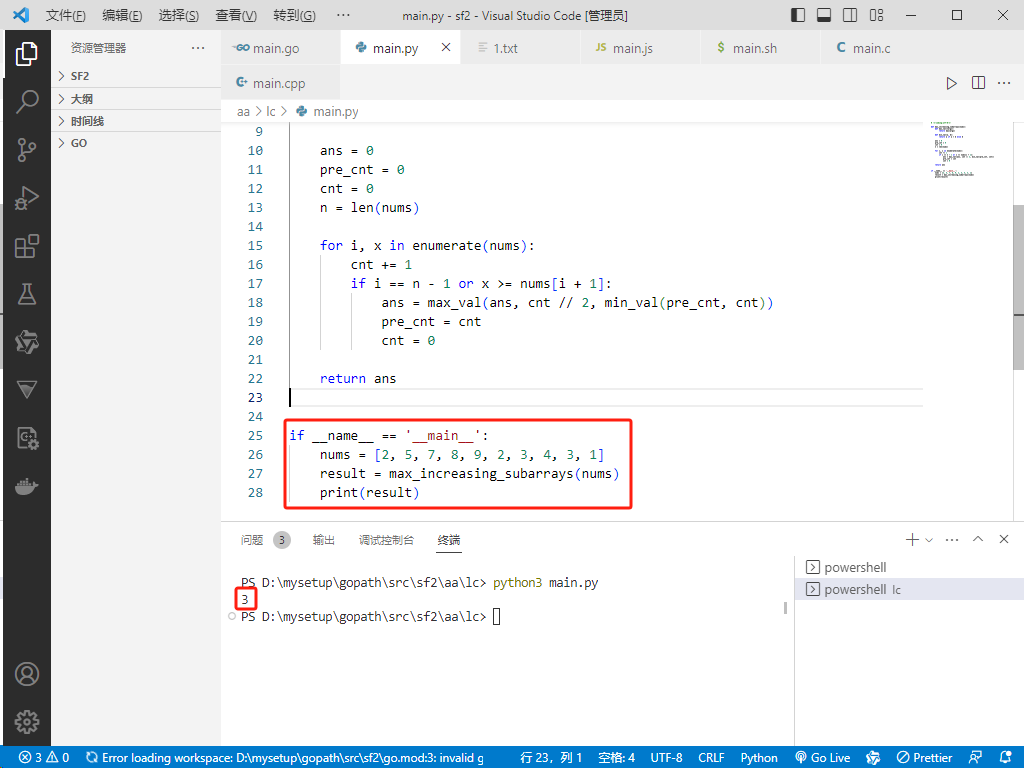
if __name__ == '__main__':
    nums = [2, 5, 7, 8, 9, 2, 3, 4, 3, 1]
    result = max_increasing_subarrays(nums)
    print(result)