2025-05-30：统计平衡排列的数目。用go语言，给定一个数字字符串 num，如果该字符串中所有位于奇数索引位置的数字之和与所有位于偶数索引位置的数字之和相等，则称这个字符串是“平衡”的。

现在需要求出由 num 的所有不同字符排列中，满足“平衡”条件的字符串个数。

由于结果可能非常大，请将最终结果对 1000000007 取模后返回。

2 <= num.length <= 80。

num 中的字符只包含数字 ‘0’ 到 ‘9’ 。

输入：num = “123”。

输出：2。

解释：
num 的不同排列包括： “123” ，“132” ，“213” ，“231” ，“312” 和 “321” 。

它们之中，“132” 和 “231” 是平衡的。所以答案为 2 。

题目来自力扣3343。

解决思路

这是一个组合数学和动态规划结合的问题。我们需要考虑以下几点：

1. 数字频率统计：统计每个数字（0-9）在字符串中出现的次数。
2. 总和检查：所有数字的总和必须是偶数，否则不可能平衡，直接返回0。
3. 目标值：平衡要求奇数位和偶数位的和相等，因此目标值是总和的一半。
4. 排列组合：我们需要计算将数字分配到奇数位和偶数位，使得奇数位的数字之和等于目标值，同时考虑数字的重复和排列组合。

详细步骤

1. 统计数字频率和总和：

   • 遍历字符串 num，统计每个数字（0-9）出现的次数，存储在数组 cnt 中。
   • 计算所有数字的总和 tot。如果 tot 是奇数，直接返回0，因为无法分成两个相等的和。

2. 预处理组合数：

   • 计算组合数 C(n, k)，用于后续分配数字到奇数位和偶数位的组合计算。这里 n 是奇数位的最大可能数量（(len(num)+1)/2），k 是选择的数量。
   • 使用动态规划计算组合数，利用递推式 C(n, k) = C(n-1, k) + C(n-1, k-1)。

3. 动态规划求解：

   • 定义 f[curr][oddCnt] 表示当前数字和为 curr，且已经分配了 oddCnt 个数字到奇数位时的方案数。
   • 初始化 f[0][0] = 1，表示初始状态（和为0，分配0个数字到奇数位）有一种方案。
   • 按数字从小到大（0到9）逐步更新动态规划表：
     • 对于数字 i，尝试将其分配到奇数位和偶数位：
       • 分配到奇数位的数量 j 可以是 0 到 min(cnt[i], oddCnt)。
       • 分配到偶数位的数量是 cnt[i] - j。
       • 更新 f[curr][oddCnt] 时，需要考虑所有可能的 j，并乘以组合数（选择奇数位和偶数位的方案数）。
   • 最终目标是 f[target][maxOdd]，其中 target 是总和的一半，maxOdd 是奇数位的最大数量。

4. 结果提取：

   • 动态规划完成后，f[target][maxOdd] 就是满足条件的平衡排列数目。

时间复杂度和空间复杂度

• 时间复杂度：
  • 组合数预处理：O(maxOdd^2)，其中 maxOdd 是奇数位的最大数量（最多约40）。
  • 动态规划：
    • 外层循环遍历数字（0-9，共10次）。
    • 内层循环遍历 oddCnt 和 curr，最坏情况下是 O(target * maxOdd)。
    • 对于每个 (curr, oddCnt)，还需要遍历 j（最多约80次）。
  • 总时间复杂度：O(10 * target * maxOdd * 80) ≈ O(10 * 2000 * 40 * 80) ≈ O(64,000,000)。由于 num.length <= 80，target 最多是 9*80/2 = 360，实际更小。
• 空间复杂度：
  • 组合数表：O(maxOdd^2) ≈ O(1600)。
  • 动态规划表：O(target * maxOdd) ≈ O(360 * 40) ≈ O(14,400)。
  • 总空间复杂度：O(target * maxOdd)。

Go完整代码如下：

package main

import (
	"fmt"
)

const MOD = 1_000_000_007

func countBalancedPermutations(num string) int {
	tot, n := 0, len(num)
	cnt := make([]int, 10)
	for _, ch := range num {
		d := int(ch - '0')
		cnt[d]++
		tot += d
	}
	if tot%2 != 0 {
		return 0
	}

	target := tot / 2
	maxOdd := (n + 1) / 2
	comb := make([][]int, maxOdd+1)
	for i := range comb {
		comb[i] = make([]int, maxOdd+1)
		comb[i][i], comb[i][0] = 1, 1
		for j := 1; j < i; j++ {
			comb[i][j] = (comb[i-1][j] + comb[i-1][j-1]) % MOD
		}
	}

	f := make([][]int, target+1)
	for i := range f {
		f[i] = make([]int, maxOdd+1)
	}
	f[0][0] = 1

	psum, totSum := 0, 0
	for i := 0; i <= 9; i++ {
		/* 前 i 个数字的数目之和 */
		psum += cnt[i]
		/* 前 i 个数字的元素之和 */
		totSum += i * cnt[i]
		for oddCnt := min(psum, maxOdd); oddCnt >= max(0, psum-(n-maxOdd)); oddCnt-- {
			/* 偶数位需要填充的位数 */
			evenCnt := psum - oddCnt
			for curr := min(totSum, target); curr >= max(0, totSum-target); curr-- {
				res := 0
				for j := max(0, cnt[i]-evenCnt); j <= min(cnt[i], oddCnt) && i*j <= curr; j++ {
					/* 当前数字在奇数位填充 j 位，偶数位填充 cnt[i] - j 位 */
					ways := comb[oddCnt][j] * comb[evenCnt][cnt[i]-j] % MOD
					res = (res + ways*f[curr-i*j][oddCnt-j]%MOD) % MOD
				}
				f[curr][oddCnt] = res % MOD
			}
		}
	}

	return f[target][maxOdd]
}

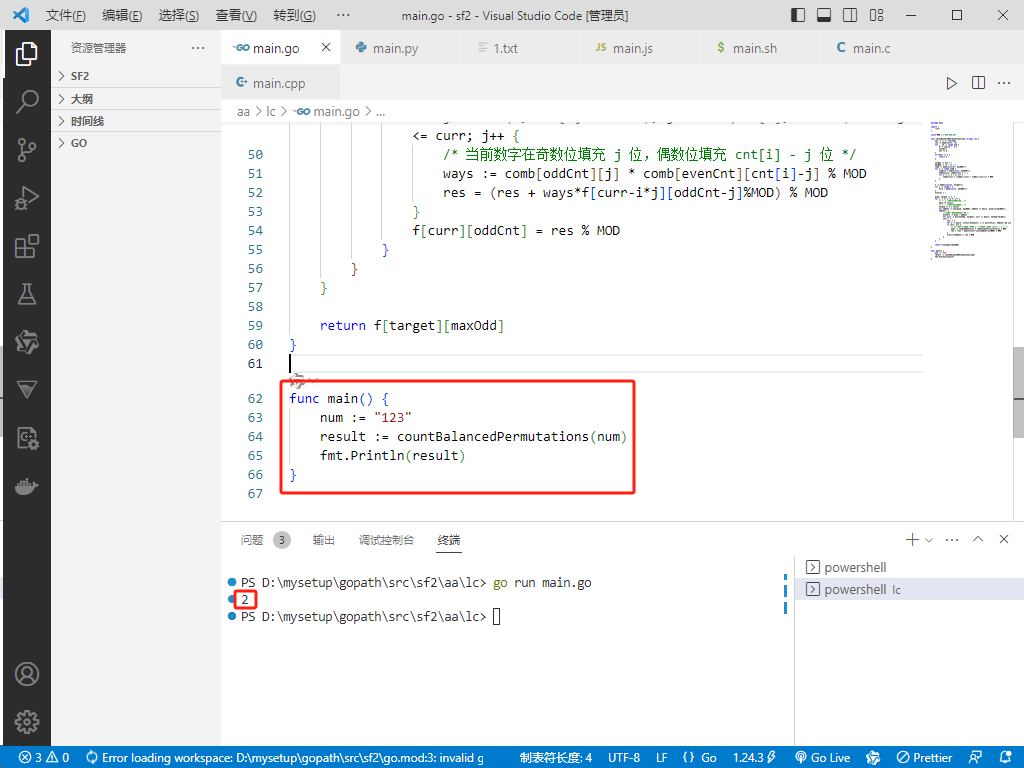
func main() {
	num := "123"
	result := countBalancedPermutations(num)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

MOD = 10**9 + 7

def min(a, b):
    return a if a < b else b

def max(a, b):
    return a if a > b else b

def countBalancedPermutations(num: str) -> int:
    tot = 0
    n = len(num)
    cnt = [0] * 10
    for ch in num:
        d = int(ch)
        cnt[d] += 1
        tot += d
    if tot % 2 != 0:
        return 0

    target = tot // 2
    maxOdd = (n + 1) // 2

    # 计算组合数 comb[i][j] 表示 C(i, j)
    comb = [[0] * (maxOdd + 1) for _ in range(maxOdd + 1)]
    for i in range(maxOdd + 1):
        comb[i][0] = 1
        comb[i][i] = 1
        for j in range(1, i):
            comb[i][j] = (comb[i-1][j] + comb[i-1][j-1]) % MOD

    # f[curr][oddCnt] 表示当前和为 curr，奇数位填充 oddCnt 个数字的方案数
    f = [[0] * (maxOdd + 1) for _ in range(target + 1)]
    f[0][0] = 1

    psum = 0  # cnt 的前缀和
    totSum = 0  # 数字之和前缀和
    for i in range(10):
        psum += cnt[i]
        totSum += i * cnt[i]

        oddCnt_start = max(0, psum - (n - maxOdd))
        oddCnt_end = min(psum, maxOdd)

        # 从大到小遍历避免重复计算覆盖
        for oddCnt in range(oddCnt_end, oddCnt_start - 1, -1):
            evenCnt = psum - oddCnt
            curr_start = max(0, totSum - target)
            curr_end = min(totSum, target)
            for curr in range(curr_end, curr_start - 1, -1):
                res = 0
                j_start = max(0, cnt[i] - evenCnt)
                j_end = min(cnt[i], oddCnt)
                for j in range(j_start, j_end + 1):
                    if i * j > curr:
                        break
                    ways = comb[oddCnt][j] * comb[evenCnt][cnt[i] - j] % MOD
                    res = (res + ways * f[curr - i * j][oddCnt - j]) % MOD
                f[curr][oddCnt] = res

    return f[target][maxOdd]


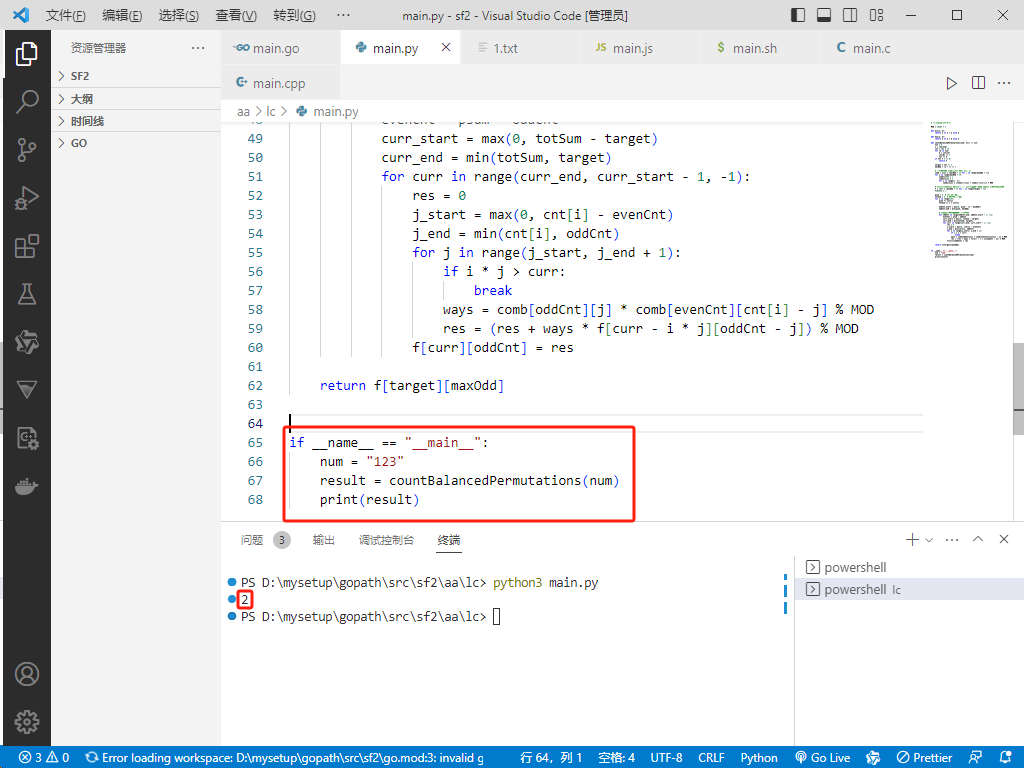
if __name__ == "__main__":
    num = "123"
    result = countBalancedPermutations(num)
    print(result)